Teilaufgabe 1: Physikalische Grundlagen der Röntgenspektroskopie
a) Der grundsätzliche Aufbau einer Röntgenröhre ist in folgender Skizze dargestellt:
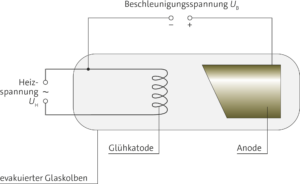
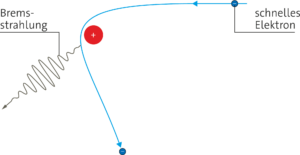
b) Das Spektrum der Röntgenstrahlung besteht aus zwei Teilen: dem kontinuierlichen Spektrum, das durch die Bremsstrahlung erzeugt wird, und den Linien, die vom Anodenmaterial abhängen. Die Bremsstrahlung kommt zustande, wenn ein Elektron sehr schnell in das Anodenmaterial eindringt und von einem Atomkern so stark abgelenkt wird, dass es es einen Teil seiner Bewegungsenergie verliert und als Strahlungsquant abgibt. Je nach der Stärke der Ablenkung, hat das Strahlungsquant eine andere Energie, weshalb dieses Spektrum kontinuierlich ist.
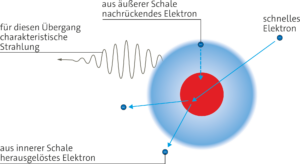
Die charakteristische Röntgenstrahlung ist lediglich ein Linienspektrum, welches dadurch entsteht, dass ein Elektron mit hoher Geschwindigkeit auf ein Atom trifft und ein Elektron aus einer inneren Atomschale herausschlägt. Beim Übergang eines Elektrons von einer höheren Schale in den freigewordenen Platz wird eine für die Atomsorte charakteristische Menge Energie in Form eines Photons abgegeben.
c) Die Bragg-Bedingung kann anhand folgender Skizze hergeleitet werden:
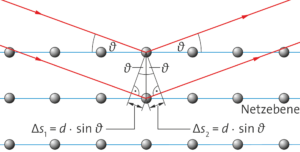
Die Röntgenwelle treffen auf die Netzebenen des Einkristalls und werden gestreut. Dabei legt die Wellenfront zwischen der Streuung an einer höheren Netzebene und der darunter einen Wegunterschied von \(\Delta s\) zurück. Durch das eingezeichnete Dreieck lässt dieser sich durch den Abstand der Netzebenen d und den Winkel \(\theta\) ausdrücken: \( \Delta s = d \cdot \sin(\theta) \). Wie aus der Skizze ersichtlich, muss die Wellenfront nach der Reflexion an der tieferen Netzebene erneut den Wegunterschied \( \Delta s \) zurücklegen, sodass der gesamte Gangunterschied zwischen den Wellenfronten \( 2\cdot \Delta s = 2 \cdot d \cdot \sin(\theta) \) beträgt. Konstruktive Interferenz tritt auf, wenn der Gangunterschied ein ganzzahliges Vielfaches der Wellenlänge ist:
\( n \cdot \lambda = 2 \cdot d \cdot \sin(\theta) \) mit \( n = 1;2;3;…\)
Die Drehkristallmethode misst die Röntgenstrahlung für verschiedene Winkel ϑ. Die Messzeit ∆t muss dabei immer gleich sein, sonst kann man die Intensität der Röntgenstrahlung nicht vergleichen.
Wenn der Winkelbereich \( 3° \leq \theta \leq 45°\) in Schritten von \( \Delta = 0,2° \) abgegangen wird, werden insgesamt \( n =\frac{45°-3°}{0,2°} +1 = 211 \) Messwerte aufgenommen.
Der gemessene Wellenlängenbereich \(\lambda_{\text{min}} \leq \lambda \leq \lambda_{\text{max}} \) lässt sich aus dem Netzebenenabstand \( d= 0,201 \, \text{nm} \) des LiF-Kristalls bestimmen:
\( \lambda_{\text{min}} =2 \cdot (2,01 \cdot 10^{-10} \, \text{m}) \cdot \sin(3°) = 2,10 \cdot 10^{-11} \, \text{m} \)
\( \lambda_{\text{max}} = 2 \cdot (2,01 \cdot 10^{-10} \, \text{m}) \cdot \sin(45°) = 2,84 \cdot 10^{-11} \, \text{m} \)
Die Röntgenstrahlung mit der kürzesten Wellenlänge kommt zustande, wenn ein Elektron die ganze Beschleunigungsspannung \(U_B\) in Bewegungsenergie umwandelt und diese als ein Strahlungsquant mit der Wellenlänge \(\lambda_{Gr}\) aussendet. Dann gilt:
\(h\cdot \frac{c}{\lambda_{Gr}} = e \cdot U_B \Leftrightarrow \lambda_{Gr} = \frac{h \cdot c}{e \cdot U_B}
Für eine Beschleunigungsspannung von \(U_B = 25 \, \text{kV} \) ergibt sich die Grenzwellenlänge:
\( lambda_{Gr} = \frac{6,63 \cdot 10^{-34} \, \text{Js} \cdot 3,00 \cdot 10^8 \frac{\text{m}}{\text{s}} }{1,60 \cdot 10^{-19} \, \text{C} \cdot 2,50 \cdot 10^4 \, \text{V} } = 4,97 \cdot 10^{-11} \text{m} \).
Diese Grenzwellenlänge liegt im Bereich der bei der Messung erfassten Wellenlängen: \( λ_{\text{min}} ≤ 4,97 ⋅10^{−11} \, \text{m} ≤ λ_{\text{max}} \)
Teilaufgabe 2: Sortierung des Periodensystems durch Bestimmung der Ordnungszahlen der Elemente
a) Anhand des Kupfer- Röntgenspektrums lassen sich die Wellenlänge von folgenden Linien bestimmen:
K\(_{\beta}\)-Linie: \(\lambda_{K_{\beta}} = 0,140 \, \text{nm} = 1,40 \cdot 10^{-10} \, \text{m} \)
K\(_{\alpha}\)-Linie: \(\lambda_{K_{\alpha}} = 0,154 \, \text{nm} = 1,54 \cdot 10^{-10} \, \text{m} \)
Die Energiedifferenz dieser beiden Linien entspricht gerade der Energiedifferenz \(\Delta E_{ML} \) der L- und M-Schale:
\(\Delta E_{ML} = h \cdot (\frac{c}{\lambda_{K_{\beta}}} -\frac{c}{\lambda_{K_{\alpha}}} = 6,63 \cdot 10^{-34} \, \text{Js} \cdot \frac{3,00 \cdot 10^8 \frac{\text{m}}{\text{s}}}{1,40 \cdot 10^{-10} \, \text{m}} – \frac{3,00 \cdot 10^8 \frac{\text{m}}{\text{s}} }{1,54 \cdot 10^{-10} \, \text{m}} = 1,29 \cdot 10^{-16} \, \text{J} = 0,81 \, \text{keV} \)
b) Messwerte:
| Z-1 : | 12 | 19 | 23 | 26 | 29 | 39 |
| \(\lambda_{K_{\alpha}}\) in m: | \(8,36 \cdot 10^{-10}\) | \(3,37 \cdot 10^{-10}\) | \(2,30 \cdot 10^{-10}\) | \(1,80 \cdot 10^{-10}\) | \(1,45 \cdot 10^{-10}\) | \(0,794 \cdot 10^{-10}\) |
| \(\frac{1}{\sqrt{\lambda_{K_{\alpha}}}} \) in \(\frac{1}{\sqrt{m}}\) | \(3,45 \cdot 10^4\) | \(5,45 \cdot 10^4\) | \(6,59 \cdot 10^4\) | \(7,45 \cdot 10^4\) | \(8,30 \cdot 10^4\) | \(11,2 \cdot 10^4\) |
Grafische Auswertung:
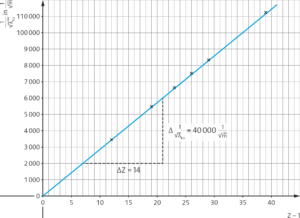
Es lässt sich ein proportionaler Zusammenhang zwischen den Größen \(\frac{1}{\sqrt{\lambda_{K_{\alpha}}}} \) und \((Z-1)\) finden.
Die Steigung der geraden kann anhand des Steigungsdreiecks bestimmt werden zu: \( \frac{ \Delta \frac{1}{\sqrt{\lambda_{K_{\alpha}}}}}{\Delta Z} = \frac{40000 \frac{1}{\sqrt{\text{m}}}}{14} = 2860 \, \frac{1}{\sqrt{m}} \). Die Proportionalitätskonstante beträgt daher \(\sqrt{C} = 2860 \frac{1}{\sqrt{m}} \).
Die \(K_{\alpha} \)-Linie von Kupfer hat eine Wellenlänge von \( \lambda_{K_{\alpha}} = 1,54 \cdot 10^{-10} \, \text{m} \), woraus folgt: \( \frac{1}{\sqrt{\lambda_{K_{\alpha}}}} = \frac{1}{\sqrt{1,54 \cdot 10^{-10} \, \text{m}}} = 8,06 \cdot 10^4 \, \frac{1}{\sqrt{\text{m}}} \).
Aus dem Diagramm kann man somit für Kupfer ablesen: \(Z-1 = 28 \), also hat Kupfer die Ordnungszahl \(Z=29\).
Teilaufgabe 3: Extrem seltene Elemente und ihre Entstehung
a) Die Zerfallsgleichung für das Isotop \(^{98}\text{Tc} \) lautet: \(^{98}\text{Ru} : \, ^{98}\text{Tc} \overset{\beta^-} \longrightarrow \, ^{98}\text{Ru} + \, ^{0}_{-1}e + \bar{\nu}_e \)
Die Zerfallsgleichung für das Isotop \(^{97}\text{Tc} \) lautet: \(^{97}\text{Mo} : \, ^{97}\text{Tc} \overset{\beta^+} \longrightarrow \, ^{97}\text{Mo} + \, ^{0}_{+1}e + \nu_e \)
Die längste Halbwertszeit unter den Technetiumisotopen besitzt \(^{98}\text{Tc} \) mit \(T_{1/2} = 4,20 \cdot 10^6 \, \text{a} \). Ein Zwanzigstel des Erdalters \(\frac{1}{20} t_E\) beträgt \(2,5 \cdot 10^8 \, \text{a}\).
Damit lässt sich aus dem Zerfallsgesetz der Anteil der noch nicht zerfallenen \(^{98}\text{Tc} \)-Kerne bestimmen:
\( \frac{N\cdot \frac{1}{20} t_E }{N_0} = (\frac{1}{2})^{\frac{2,5 \cdot 10^8 \, \text{a} }{4,2 \cdot 10^6 \, \text{a}} }= 1,2 \cdot 10^{-18} \).
Eine mögliche Kernreaktion, durch die in der Molybdän-Folie Technetiumisotope enstanden sein könnten lautet z.B. \(^{97}\text{Mo} + ^{2}\text{H} \rightarrow \, ^{98}\text{Tc} + \, ^{1}n \).
Der natürliche Entstehungsweg von \(^{99}\text{Tc} \) geht von der spontanen Spaltung eines Urankerns aus. Die anderen Nuklide, die in dieser Zerfallskette vorkommen, haben eine maximale Halbwertszeit von etwa 65 Stunden. Das \(^{99}\text{Tc} \) am Ende der Zerfallskette hat dagegen eine Halbwertszeit von \(T_{1/2} = 2,11 \cdot 10^5 \, \text{a} \). Im Uranerz sind die Nuklide dieses sehr seltenen Vorgangs mit kurzen Halbwertszeiten nicht nachweisbar, weil sie nur sehr kurz dort existieren, bevor sie zu dem viel langlebigeren \(^{99}\text{Tc} \) zerfallen.
b) Bei der Zerlegung eines schweren Atomkerns in Abbildung 7 sieht man, dass die meisten Spaltprodukte eine Massenzahl um 140 haben. Die Promethiumisotope, die am längsten existieren (\(^{145}\text{Pm} \) bis \(^{147}\text{Pm} \) ), gehören zu dieser Gruppe. Deshalb findet man sie oft in den Spaltprodukten eines Kernreaktors.
Es gibt lediglich \(m = 0,570 \, \text{kg} \) Promethium natürlichen Ursprungs in der Erdkruste, was \( N= 6,02 \cdot 10^{23} \cdot \frac{0,570 \text{kg}}{0,147 \text{kg}} = 2,33 \cdot 10^{24} \, ^{147}\text{Pm} \)-Atomkernen entspricht. Mit der Halbwertszeit von Promethium \(T_{1/2} = 2,625 \cdot 10^5 \, \text{a} = 8,28 \cdot 10^7 \, \text{s} \) lässt sich die Aktivität A wie folgt bestimmen:
\( A = \frac{\ln{(2)}}{T_{1/2}} \cdot N = \frac{\ln(2)}{8,28 \cdot 10^7 \, \text{s} } \cdot 2,33 \cdot 10^{24} = 1,95 \cdot 10^{16} \, \text{Bq} \).
Teilaufgabe 4: Das extraterrestrische Vorkommen von Promethium
a) Promethium zerfällt mit einer Halbwertszeit von 17,7 Jahren im Vergleich zur Lebensdauer des Sterns sehr schnell. Da der Stern bereits etwa 5 Milliarden Jahre alt ist, muss das Promethium dort immer wieder neu entstehen, damit es nicht ganz verschwindet.
b) Die seltenen Elemente, die neben Promethium im Periodensystem stehen, und Promethium selbst, das im Stern gefunden wurde, kommen durch die Zerlegung großer Mengen Uranisotope mit langer Lebensdauer an der Oberfläche des Sterns zustande. Deshalb sollte man auch die Spektrallinien des Urans im Lichtspektrum des Sterns gut sehen können.