Teilaufgabe 1: Grundlagen zum Induktionsgesetz
a) Induktionsspannung tritt auf, wenn sich die vom Magnetfeld durchsetzte Fläche eines Leiterkreises zeitlich ändert, was durch den ersten Term beschrieben wird. Dies gilt ebenso für die Induktionsspannung, wenn sich die Stärke 𝐵 des magnetischen Feldes, das die Fläche eines Leiterkreises senkrecht durchsetzt, zeitlich verändert, was durch den zweiten Term beschrieben wird. Um den ersten Fall zu veranschaulichen, könnte man eine Leiterschleife in einem Magnetfeld rotieren lassen. In Bezug auf den zweiten Fall könnte man eine Induktionsspule in eine Feldspule legen und die Stärke 𝐵 des magnetischen Feldes der Feldspule zeitlich variieren.
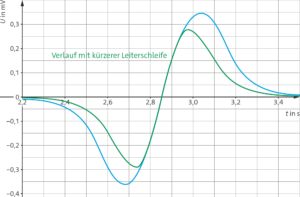
b) Ein (qualitativ) passendes t-U-Diagramm sieht wie folgt aus:

c) Der Eintritt der Leiterschleife mit einer Windungszahl \(n = 1\) in das Magnetfeld führt zu einer zeitlichen Änderung der von den Feldlinien durchsetzten Fläche. Dabei bleibt die Stärke 𝐵 des Magnetfeldes konstant. Infolgedessen ist im Rahmen des in der Aufgabenstellung genannten Induktionsgesetzes ausschließlich der erste Term mit der Windungszahl \(n = 1\) relevant, während der zweite Term stets null ist. Dies liegt daran, dass sich die Stärke 𝐵 des Magnetfeldes nicht zeitlich ändert.
Die Längenänderung \(\Delta\)s des sich pro Zeit \(\Delta\)T in Magnetfeld befindlichen Teils der Leiterschleife kann benutzt werden um einen Ausdruck für die Fläche \(\Delta\)A zu finden: \(\Delta A = \Delta s \cdot b\) Mit der gegebenen Gleichung folgt:
\(U_{\text{ind}} = -B \cdot \frac{\Delta A}{\Delta t} = – B \cdot \frac{b\cdot\Delta s}{\Delta t} =- B \cdot b \cdot \frac{\Delta s}{\Delta t} = – B \cdot b \cdot v \)
Teilaufgabe 2: Fahrbahn-Versuche zum Induktionsgesetz
a) Zu Beginn ist die gemessene Spannung negativ und nahe null. Sie sinkt mit zunehmender Zeit und erreicht ihr Minimum bei \(t = 2,68 \, \text{s}\) mit einem Spannungswert von \( U_{\text{min}} = -0,36 \, \text{mV} \). Im Folgenden steigt die Spannung wieder an und erreicht bei \(t = 2,85 \, \text{s}\) einen Nullpunkt. Die Spannung steigt weiter an und erreicht bei \(t = 3,04\, \text{s}\) den maximalen Spannungswert von \(U_{\text{max}} = 0,35\, \text{mV}\) . Danach fällt die Spannung wieder ab und nähert sich dem Wert null an.
b) Aufgrund der Drei-Finger-Regel der linken Hand wirkt die Lorentzkraft im gesamten Leiter immer nach unten und ist proportional zur Stärke 𝐵 des magnetischen Feldes. Im homogenen Feldbereich, in dem sich das rechte Leiterstück in beiden Abbildungen befindet und die gleiche Feldstärke \(B_{\text{max}}\) vorliegt, wirkt eine konstante Lorentzkraft. Das linke Leiterstück liegt in beiden Abbildungen in einem Bereich des Magnetfelds mit \( B < B_{\text{max}}\). Das linke Leiterstück ist in Abbildung 5c einem stärkeren Magnetfeld ausgesetzt, weshalb eine stärkere Lorentzkraft wirkt. Wenn die Differenz der Lorentzkräfte im linken und rechten Leiterstück größer ist, ist auch eine höhere Spannung messbar, weshalb das zu messende Spannungssignal in Abbildung 5b höher ist als in Abbildung 5c.
Im rechten Teil der Leiterschleife herrscht ein konstantes Magnetfeld, weshalb auch die Lorentzkraft konstant ist und ihren maximalen Wert annimmt. Indem die Leiterschleife nach rechts bewegt wird, steigt auch in der linken Hälfte die Stärke des Magnetfelds und damit auch die Lorentzkraft. Dadurch sinkt die Differenz zwischen den wirkenden Kräften in beiden Teilen der Schleife, wodurch die gemessene Spannung sinkt.
Die Spannung erreicht ihren minimalen Wert von \( U= 0 \, \text{mV} \), wenn die Leiterschleife sich genau mittig im Magnetfeld befindet und auf beide Seiten die gleiche Lorentzkraft wirkt.
c) In der folgenden Tabelle sind alle Werte eingetragen. Die Spannungswerte entsprechen den gemittelten Werten der Spannungsmaxima und -minima.
| Messung | 1 | 2 | 3 | 4 |
| \(\Delta t \) in s | 0,22 | 0,27 | 0,38 | 0,50 |
| \(U_{\text{max}}\) in mV | 0,41 | 0,36 | 0,25 | 0,19 |
| \(v\) in \(\frac{\text{cm}}{\text{s}}\) | 45 | 37 | 26 | 20 |
Anhand der Werte lässt sich folgendes Diagramm erstellen:
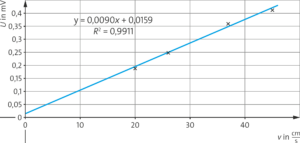
Es ist ein linearer Zusammenhang zwischen der Spannung und der Geschwindigkeit erkennbar: \( U_{\text{max}} ~ v\). Aus der Gleichung \( U_{\text{max}} = v \cdot B_{\text{max}} \cdot b \) mit der Steigung \( m = 0,0090 \, \frac{\text{mV}}{\frac{\text{cm}}{\text{s}}} \) und \( b = 3,2 \, \text{cm}\) folgt:
\( U_{\text{max}} = v \cdot B_{\text{max}} \cdot b \Leftrightarrow B_{\text{max}} = \frac{U_{\text{max}}}{v \cdot b} = 9,0 \,\frac{\rm \textmu V}{\frac{\text{cm}}{\text{s}}} \cdot \frac{1}{3,2 \, \text{cm}} \approx 28 \, \text{mT} \)
d) Anhand der Abbildung und den gemessenen Spannungswerten kann man darauf schließen, dass der Hufeisenmagnet die gleiche Ausrichtung wie bei den vorherigen Experiment hat (Nordpol vorne, Südpol hinten). Da der Verlauf der gemessenen Spannung beim zweiten Magneten an der \(x\)-Achse gespiegelt ist und damit das inverse Vorzeichen besitzt, muss der Hufeisenmagnet genau umgekehrt ausgerichtet sein (Nordpol hinten, Südpol vorne).
Obwohl die Bewegung gleichförmig ist, sind die Extrema beim zweiten Hufeisenmagnet größer, woraus sich schließen lässt, dass der Magnet eine größere Feldstärke \(B\) verursacht.
Die Geschwindigkeit lässt sich anhand der Verdunklungszeit \(\Delta t = 0,56 \, \text{s}\) und der Strecke \(\Delta s = 10 \, \text{cm}\) berechnen:
\( v = \frac{\Delta s}{\Delta t} = \frac{10 \, \text{cm}}{0,56 \, \text{s}} \approx 18 \frac{\text{cm}}{\text{s}} \). Die Nulldurchgänge können abgelesen werden bei \( t \approx 1,28 \, \text{s}\) und \( t \approx 2,69 \, \text{s}\), woraus ein zeitlicher Abstand von \( t_{\text{Abstand}} \approx 1,4 \, \text{s}\) folgt. Für den räumlichen Abstand zwischen den beiden Hufeisenmagneten folgt daraus:
\( D = t_{\text{Abstand}} \cdot v = 1,4 \, \text{s} \cdot 18 \, \frac{\text{cm}}{\text{s}} \approx 25 \, \text{cm} \)
e) In den Abbildungen 3 und 8b gibt es zwei Spannungsextrema, wobei das Erste im negativen, das Zweite im positiven Spannungsbereich liegt. Außerdem geben bei beiden Abbildungen die Spannungswerte für \(t< 2,2\,{\rm s}\) und \(t > 3,4\,{\rm s}\) gegen \(U = 0\,{\rm V}\).
Das Diagramm in Abbildung 8b weist ein Plateau zwischen den beiden Extrema auf, welches ca. zwischen \(t = 2,96\,{\rm s}\) und \(t = 3,24\,{\rm s}\) liegt und einen Spannungswert von nahezu \(U = 0\,{\rm V}\) hat. Außerdem ist das Spannungssignal kurz vor und hinter dem Plateau weniger steil als in Abbildung 3.
Der maßgebliche Unterschied zwischen beiden Versuchsaufbauten ist der Eisenkern, welcher einen größeren Bereich mit homogenem Magnetfeld erzeugt. Dadurch ist in der Leiterschleife für einen längeren Zeitpunkt keine Induktionsspannung messbar, wodurch das beschriebene Plateau entsteht.