Teilaufgabe 1: Interferenz am Doppelspalt
a) Alle Punkte auf einer Wellenfront sind Ausgangspunkt für eine Elementarwelle, welche die selbe Geschwindigkeit und Frequenz wie die ursprüngliche Wellenfront besitzt. Die neue Wellenfront ergibt sich als Einhüllende aus den Elementarwellen. Beim Doppelspalt kann jeder Spalt als Ausgangspunkt einer Elementarwelle betrachtet werden, die sich kreisförmig ausbreitet. Wenn die Elementarwellen, die an den Spalten entstanden sind, sich treffen und konstruktiv interferieren (maximal verstärken), treten Orte maximaler Helligkeit auf. Wenn die Elementarwellen destruktiv interferieren (sich gegenseitig auslöschen) treten Orte minimaler Helligkeit auf.
b) Die mathematische Bedingung für konstruktive Interferenz ist, dass der Gangunterschied \( \Delta s\) der beiden Wellen die Differenz eines ganzzahligen Vielfaches der Wellenlänge und einer halben Wellenlänge ist. Dies wird durch die gegebene Gleichung ausgedrückt.
Gleichung 2 ist nur dann erfüllt, wenn die Lichtwege, die durch Pfeile dargestellt werden, parallel sind. In diesem Fall ist das grau unterlegte Dreieck rechtwinklig und der Winkel \(\alpha_n\) liegt der Seite \(\Delta s\) gegenüber.
c) Aus Gleichung (2) folgt der Zusammenhang \( \alpha_n = \sin^{-1}({\frac{\Delta s}{g}}) \). Unter Verwendung von Gleichung (3) folgt \(d_n = a \cdot \tan{(\sin^{-1}({\frac{\Delta s}{g})})} \). Der Buchstabe „A“ markiert die Stelle des Minimums, das zu \(n=2\) gehört. Die erste Gleichung wird damit zu \( \Delta s = 1,5 \cdot \lambda \).
Damit folgt \(d_2 = a \cdot \tan{(\sin^{-1}({\frac{1,5 \cdot \lambda}{g}}))} \).
Das Einsetzen der gegebenen Werte liefert:
\( d_2 = 2,5 \, \text{m} \cdot \tan{(\sin^{-1}({\frac{1,5 \cdot 537 \cdot 10^{-9} \, \text{m}}{1,0 \cdot 10^{-4} \, \text{m}})})} \).
Die Stelle, die mit „A“ markiert ist, gehört zum Skalenwert 2,0 cm. Hier tritt ein Maximum auf, wenn:
(i) der Abstand \(a\) zwischen Schirm und Doppelspalt angepasst wird,
(ii) die Wellenlänge \(\lambda\) des Lasers entsprechend verändert wird,
(iii) der Spaltabstand \(g\) angepasst wird.
d) Wenn ein einzelner Absorber verwendet wird, ist zwar noch das zu erwartende Interferenzmuster erkennbar, es kann aber keine kontinuierliche Intensitätsverteilung beobachtet werden. Die stattdessen entstehenden Punkte sind sind je nach Bereich gehäuft oder gar nicht zu sehen. Wenn mehr Absorber im Strahlengang positioniert werden, sind die verschiedenen Bereiche zunehmend schlechter voneinander abgrenzbar. Das Versuchsergebnis in Abbildung 4 zeigt, dass Licht sowohl als klassische Welle, als auch als klassisches Teilchen beschrieben werden kann. Die sich traditionell ausschließenden Eigenschaften treten je nach Versuchsaufbau unterschiedlich stark auf. Bei intensivem Licht sind die Welleneigenschaften gut erkennbar, während bei sehr schwachem Licht der Teilchencharakter des Lichts deutlicher wird. Insgesamt lässt sich Licht nicht allein durch das Modell der Welle oder des Teilchens erklären.
Teilaufgabe 2: Der Photoeffekt
a) Der Photoeffekt bewirkt, dass aus der Zinkplatte Elektronen austreten, die im elektrischen Feld beschleunigt werden und sich zur Anode bewegen. Das Stromstärkemessgerät kann diesen elektrischen Strom messen.
Indem die Quecksilberdampflampe näher an die Zinkplatte gebracht wird, erhöht sich die Photonenintensität, wodurch mehr Elektronen pro Zeiteinheit aus der Platte gelöst werden. Dadurch erhöht sich die gemessene elektrische Stromstärke. Damit Elektronen aus der Zinkplatte austreten, muss das Licht eine hinreichend kleine Wellenlänge haben. Demnach wird der Anteil des Lichtspektrums mit geringerer Wellenlänge von der Glasplatte absorbiert.
b) Beim Photoeffekt absorbiert ein einzelnes Elektron genau ein einzelnes Photon, wobei die übertragene Energie von der Photonenenergie \(E = h \cdot f \) abhängt. Das bedeutet, dass der Energieaustausch quantisiert ist.
c) Die Spektrallinie P hat die kleinste Wellenlänge beziehungsweise die Photonen mit der größten Energie.
Damit beim Photoeffekt Elektronen aus der Zinkplatte gelöst werden, muss ein Photonen bei der Wechselwirkung mindestens die Auslöseenergie übertragen:
Mit der Formel \( E = h \cdot f = h \cdot \frac{c}{\lambda} \) ergibt sich für die maximale Wellenlänge: \( \lambda_{\text{max}} = h \cdot \frac{c}{E_A} \).
Mit den gegebenen Werten folgt:
\( \lambda_{\text{max}} = 6,63 \cdot 10^{-34} \, \text{Js} \cdot \frac{3,00 \cdot 10^8 \, \frac{\text{m}}{\text{s}}}{4,34 \cdot 1,60 \cdot 10^{-19} \text{J}} = 2,86 \cdot 10^{-7} \, \text{m} = 286 \, \text{nm} \).
Im angegebenen Wellenlängenintervall ist keine Spektrallinie mit einer Wellenlänge \( \lambda \leq 286 \, \text{nm} \) sichtbar. Daraus folgt, dass es eine Spektrallinie mit \( \lambda < 200 \, \text{nm} \) geben muss.
d) Schaltbild
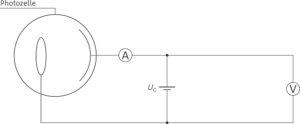
Die maximale kinetische Energie \(E_{kin,max} \) der aus der Kathode freigesetzten Elektronen hängt mit dem kleinsten Wert der Gegenspannung \(U_G\) zusammen, bei dem \(I_{Ph}=0 \) gilt. Daher ist \(E_{kin,max} \), also die von einem Photon auf ein Elektron übertragene Energie \(E\) bei Lichtquelle A größer. Aus der Formel \( \lambda = h \cdot \frac{c}{E} \) ergibt sich, dass die Wellenlänge \(\lambda\) bei Lichtquelle A kleiner ist.
Laut Angaben ist die emittierte Strahlungsenergie pro Zeiteinheit bei beiden Lichtquellen gleich. Da Lichtquelle A aber eine geringere Wellenlänge \(\lambda\) hat, werden hier mehr Photonen pro Sekunde ausgesendet.
Allerdings ist für \(U_G = 0 \) der Photostrom beider Lichtquellen gleich, weshalb der Anteil jener Photonen, die ein Elektron herauslösen, bei Lichtquelle A größer.