Teilaufgabe 1: Grundlagen zum Induktionsgesetz
a) Die vorliegende Formel beschreibt, wie das Auftreten einer induzierten Spannung mit einer zeitlichen Veränderung der Stärke des äußeren magnetischen Feldes einhergeht. Dabei bleiben die Anzahl der Windungen sowie die durchsetzte Querschnittsfläche der Spule konstant.
b) Aus der Abbildung ist zu erkennen, dass sich die Magnetfeldstärke \(B\) im genannten Zeitintervall eine konstante Änderungsrate hat. Daher muss die Induktionsspannung konstant sein. Im Zeitintervall zwischen \(t = 0 \,\text{s} \) bis \(t = 4 \, \text{s} \) gilt:
\( U_{ind} = – n \cdot A \cdot \frac{\Delta B}{\Delta t} = – 400 \cdot 2,50 \cdot 10^{-3} \text{m²} \cdot \frac{40 \text{mT}}{4 \text{s}} = – 10,0 \text{mV} \).
Für das nächste Zeitintervall von \(t= 4 \text{s} \) bis \( t = 6 \text{s} \) folgt:
\( U_{ind} = – n \cdot A \cdot \frac{\Delta B}{\Delta t} = – 400 \cdot 2,50 \cdot 10^{-3} \text{m²} \cdot \frac{-40 \text{mT}}{2 \text{s}} = + 20,0 \text{mV} \).
Das Diagramm für die induzierte Spannung in Abhängigkeit der Zeit sieht wie folgt aus:
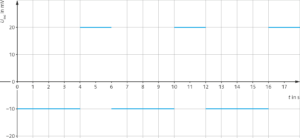
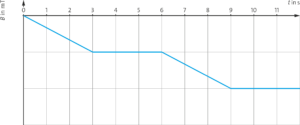
c) Damit ergibt sich das passende \(t-B-\) Diagramm für die Feldspule:
Teilaufgabe 2: Induktives Laden von Elektroautos
a) Lediglich wenn das Auto in Parkposition gebracht wird und an die Bodenspule eine Gleichspannungsquelle angeschlossen wird, entsteht eine Induktionsspannung. Dies geschieht nur während des kurzen Zeitraums, in dem eine vorübergehende Veränderung in der Stärke des magnetischen Feldes der Autospule festgestellt wird. Nach dem Parken erzeugt die Autospule keine messbare Induktionsspannung mehr, da das Magnetfeld der Bodenspule sich nicht verändert ist und daher keine Induktion in der Autospule stattfindet.
Im Fall einer Wechselspannungsquelle, die mit der Bodenspule verbunden ist, ändert sich die Stromrichtung in der Spule und damit auch das Magnetfeld kontinuierlich. Dadurch wird an den Enden der Autospule eine Wechselspannung induziert, was ermöglicht, dass die Batterie kontinuierlich geladen wird.
b) Die Periodendauer der Wechselspannung wird geringer, wenn sich ihre Frequenz erhöht. Entsprechend vergrößert sich der Quotient \( \frac{\Delta B}{\Delta t} \) und es tritt eine höhere Induktionsspannung (oder Sekundärspannung) an der Autospule auf.
Durch Vergrößern der anliegenden Primärspannung, lässt sich eine entsprechend größere Sekundarspannung erzeugen.
Teilaufgabe 3: Elektromotorische Bremse
a) Das homogene Magnetfeld hat eine Stärke \(B\) und der Stab bewegt sich mit gleichbleibender Geschwindigkeit \(v\) durch dieses hindurch. Innerhalb des Stabs führt die daraus resultierende Lorentzkraft zu einer Ladungstrennung, wodurch am einen Ende des Stabs ein Elektronenüberschuss und am anderen Ende ein -mangel entsteht. Dies führt zur Entstehung eines elektrischen Feldes zwischen den Enden, begleitet von einer nachweisbaren Induktionsspannung entlang der Schienen. Die Ladungstrennung und die Generierung des elektrischen Feldes dauern an, bis sich die Kräfte der Lorentzkraft und des elektrischen Feldes ausgleichen. Die gleichbleibende elektrische Feldstärke 𝐸 resultiert in einer konstanten Induktionsspannung.
Dieses Kräftegleichgewicht zwischen der elektrischen Feldkraft \(F_E\) und der Lorentzkraft \( F_L\) wird genutzt und eine Formel für die Induktionsspannung \(U_{\text{ind}} \) herzuleiten:
\(F_L = F_E\)
\(q \cdot v \cdot B = q \cdot E \)
Für die elektrische Feldstärke gilt \(E = \frac{U_{\text{ind}}}{l} \):
\( U_{\text{ind}} = B \cdot l \cdot v \)
Mit den gegebenen Werten ergibt sich:
\(U_{\text{ind}} = 2,5 \cdot 10^{-3} \, \text{T} \cdot 6,0 \cdot 10^{-2} \, \text{m} \cdot 1,2 \cdot 10^{-2} \, \frac{\text{m}}{\text{s}} = 1,8 \, \mathrm{\mu V}. \)
b) Die Dreifingerregel besagt, dass sich die negativen Ladungsträger am hinteren Stabende (Q), das mit der hinteren Schiene verbunden ist, bei der Ladungstrennung ansammeln.
Am vorderen Stabende (P) sind die meisten positiven Ladungsträger vorhanden. Die Ladungsträger vom hinteren Stabende (Q) bewegen sich in einem geschlossenen Stromkreis im Uhrzeigersinn, während sich im bewegten Stab die Ladungsträger vom vorderen Stabende (P) zum hinteren Stabende (Q) bewegen.
Durch die Anwendung der Drei-Finger-Regel mit der linken Hand auf die Elektronen, die sich im Stab gegen den Uhrzeigersinn bewegen, entsteht eine Kraft, die entgegen der Geschwindigkeit \(\vec{v}\) des Stabs wirkt, was zu einem Bremsvorgang führt.
c) Eine von null verschiedene Induktionsstromstärke \(I\) ist nach \( t = 0,6\)s messbar, woraus folgt, dass an den Stabenden eine nicht verschwindende Induktionsspannung anliegt. Nach dem Zusammenhang aus Aufgabenteil a) muss damit eine von null verschiedene Geschwindigkeit vorliegen, da die Größen \(B\) und \(l\) konstant sind.
Aus den beiden Formeln \( U_{\text{ind}} = B \cdot l \cdot v \) und \( U_{\text{ind}} = I \cdot R \) folgt, dass die Stromstärke proportional zur Geschwindigkeit ist: \( I \)~\( v \). Da durch die Bremskraft die Geschwindigkeit mit der Zeit abnimmt, muss auch die Stromstärke mit der Zeit kleiner werden.
d) Der Fahrer bemerkt vor allem die hohe Bremsbeschleunigung zu Beginn, da die Bremswirkung zunächst hoch ist und dann schnell abfällt. Für eine Vollbremsung bis zum Stillstand muss zusätzlich eine mechanische Bremskraft wirken, da die Bremskraft nicht mit der Zeit abnehmen sollte.