Chemie 3. Säure-Base Lösungen

Lösungen zu Check-up

Kapitel 3 Säure-Basen-Reaktionen

________________________________________________________

Seite 68

Aufgabe 1

a HCl + H₂O ⟶H₃O⁺ + Cl⁻

HCl: Säure, H₂O: Base

b Die Reaktion von HCl mit H₂O erhöht die Konzentration der Oxonium-­Ionen. Das System ist nicht mehr im Gleichgewicht, und die Neutralisationsreaktion läuft schneller ab als die Auto­protolyse, bis das Gleichgewicht wieder eingestellt ist, d. h.:

c(H₃O⁺) · c(OH⁻) = K_W

Dadurch wird c(OH⁻) kleiner als 10⁻⁷ mol · l⁻¹.

\( c{\rm (OH^-)} =  \frac {K_{\rm W}} {c{\rm (H_3O^+)}} = {\rm \frac {10^{-14}\ mol^2\ ·\ l^{-2}} {10^{-3}\ mol\ ·\ l^{-1} } } = {\rm 10^{-11} mol · l^{−1}} \)

c Die Zahl der Oxonium-Ionen aus der Autoprotolyse ist genauso groß wie die Zahl der Hydroxid-Ionen, weil letztere in der sauren Lösung nur durch die Autoprotolyse entstehen, d. h.:

c(H₃O⁺, Autoprot.) = 10⁻¹¹ mol · l⁻¹

 

Aufgabe 2

a  Der pH-Wert einer Lösung ist der negative Zehnerlogarithmus der Oxonium-Ionen-Konzentration der Lösung mit der Einheit mol · l⁻¹.
pH = − lg c(H₃O⁺)

b Gegebene Größen sind kursiv gesetzt:

c(H3O+)	c(OH−)	pH	pOH
10−6 mol · l−1	10−8 mol · l−1	6	8
10−9 mol · l−1	10−5 mol · l−1	9	5
5 · 10−3 mol · l−1	2 · 10−12 mol · l−1	2,3	11,7
5 · 10−9 mol · l−1	2 · 10−6 mol · l−1	8,3	5,7

 

Aufgabe 3

a  Bei 70 °C gilt für K_W:
K_W(bei 70 °C) = c(H₃O⁺) · c(OH⁻) = 15,88 · 10⁻¹⁴ mol² · l⁻²
In Wasser ist c(H₃O⁺) = c(OH⁻)
⇒ c(H₃O⁺) =\( \sqrt {K_{\rm W}} \) = 3,98 · 10⁻⁷ mol · l⁻¹
⇒ pH ≈ 6,4

b Da in Wasser (nicht in Lösungen!) immer c(H₃O⁺) = c(OH⁻) ist, ist Wasser auch neutral, wenn der pH­-Wert nicht gleich 7 ist.

 

Aufgabe 4

a  2 NH₃ \( \rightleftharpoons\) NH₄⁺ + NH₂⁻

b Es gilt: K_W(NH₃) = c(NH₄) · c(NH₂)
In Ammoniak ist c(NH₄⁺) = c(NH₂⁻),
d. h., c(NH₄) =  K_W(NH₃) = 10⁻¹⁶ mol · l
⇒ pH(NH₃) = −lg c(NH⁺) = 16

c Bei − 33 °C gilt:
sauer: 10⁻¹⁶ mol · l⁻¹ < c(NH₄⁺) > c(NH₂⁻)
neutral: 10⁻¹⁶ mol · l⁻¹ = c(NH₄⁺) = c(NH₂⁻)
alkalisch: 10⁻¹⁶ mol · l⁻¹ > c(NH₄⁺) < c(NH₂⁻)

 

Aufgabe 5

Sechs Schlussfolgerungen sind möglich:
– HA¹ ist eine stärkere Säure als HA².
– A⁻¹ ist eine schwächere Base als A⁻².
– pK_S(HA¹) < pK_S(HA²)
– pK_B(A⁻¹) > pK_B(A⁻²)
– Bei gleicher Konzentration c₀ ist der pH­Wert einer Lösung von HA¹ kleiner als der einer Lösung von HA², falls es sich nicht bei beiden um sehr starke oder sehr schwache Säuren handelt.
– Für die Gleichgewichtsreaktion HA¹ + A⁻² \( \rightleftharpoons \) HA² + A⁻¹ ist

\( K_{\rm C} = \frac {K_{\rm S}{\rm (HA^1)}} {K_{\rm S}{\rm (HA^2)}} > 1 \)

⇒ Das Gleichgewicht liegt rechts.

 

Aufgabe 6

a  Die Farbe des Indikators zeigt, dass die entstehende Lösung alkalisch reagiert, d. , bei der Reaktion müssen Hydroxid­-Ionen entstanden sein. Dies ist nur durch eine Reaktion der Säure H₂O mit der Base CH₃⁻ möglich:
CH₃⁻ + H₂O ⟶ OH⁻ + CH₄

Daneben entsteht CH₄ (Methan), wodurch die Gasbildung erklärt wird.

b  CH₃⁻ + H₂O ⟶ OH⁻ + CH₄

(Base 1 + Säure 2 ⟶ Base 2 + Säure 1)

 

Aufgabe 7

a Der Schüler verwechselt korrespondierende Säure­-Base­-Paare und Ampholyte. Nur für korrespondierende Säure-­Base-­Paare ist die Summe aus pK_S und pK_B gleich 14 (bei 25 °C).

b NaHCO₃ bildet in wässriger Lösung Na⁺­- und HCO₃­^–­-Ionen. Na⁺­-Ionen protolysieren nicht, haben also keinen Einfluss auf den pH­-Wert. Für den Ampholyt HCO₃⁻ ist pK_B = 7,48 und pK_S = 10,40, d. h., die Basenstärke überwiegt die Säurestärke. Die Lösung reagiert somit alkalisch.

 

Aufgabe 8

\( \frac {K_{\rm S}{\rm (HA)}} {c_0{\rm HA}} = \frac {α^2} {1 – α} \)

\( K_{\rm S}{\rm (HA)} = \frac {c{\rm (H_3O^+)}\ ·\ c{\rm (A^-)}} {c{\rm (HA)}} \)

\( α =  \frac {c{\rm (A^-)}} {c_0{\rm (HA)}} ⇒ c{\rm (A^-)} = α · {c_0{\rm (HA)}} \) 

Werden die H₃O⁺­ ­Ionen aus der Autoprotolyse des Wassers ver­nachlässigt, dann ist durch die Protolyse von HA c(H₃O⁺) = c(A⁻), d.h.:
c(H₃O⁺) = α · c₀(HA)

Aufgrund der Protolyse von HA gilt außerdem:
c(HA) = c₀(HA) − c(A⁻) = (1 − α) · c₀(HA)
⇒ K_S(HA) = \( \frac {(α\ ·\ c_0{\rm (HA)})^2\ ·\ c_0{\rm (HA)} } {1 – α} \)
K_S(HA) = \( \frac {c_0{\rm (HA)}\ ·\ α^2} {1 – α} \)
\( \frac {K_{\rm S}{\rm (HA)}} {c_0{\rm (HA)}} = \frac {α^2} {1 – α} \)

 

Aufgabe 9

a  pK_S(CH₃COOH) < pK_S(H₂CO₃). CH₃COOH ist die stärkere Säure, Gleichgewicht liegt rechts.

b pK_S(NH₄⁺) > pK_S(H₃O⁺). H₃O⁺ ist die stärkere Säure, Gleich­gewicht liegt links.

c pK_S(NH₄⁺) < pK_S(H₂O). NH₄⁺ ist die stärkere Säure, Gleichgewicht liegt rechts.

 

Aufgabe 10

a pK_S(CH₃COOH) = 4,75 ⇨ mittelstarke Säure
pH = \( \frac{1}{2} \) [pK_S − lg c₀(HA)] = 2,53

b pK_B(NH₃) = 4,75 ⇨ mittelstarke Base
pOH = \( \frac{1}{2} \)  [pK_B − lg c₀(B)] = 3,03 ⇨ pH = 10,97

c pK_B(Cl ) = 21 ⇨ sehr schwache Base ⇨ kein Einfluss auf pH
pK_S(NH₄⁺) = 9,25 ⇨ mittelstarke Säure
pH = \( \frac{1}{2} \) [pK_S − lg c₀(HA)] = 4,63

d pK_S(HNO₃) = − 1,32 ⇨ starke Säure
⇒K_S= 20,9 und K_S /c₀ ≈ 100 > 10
D. h., zur pH-Wert-Berechnung kann die Näherung für sehr starke Säure angewendet werden:
pH = −lg c₀(HNO₃) = 0,7

 

Aufgabe 11

a Eine Lösung mit pH = 9 ist alkalisch. Das steht im Widerspruch dazu, dass in der Salzsäure HCl gegenüber H₂O als Säure reagiert und dabei H₃O⁺­Ionen erzeugt werden. Der pH­-Wert der Lösung muss kleiner als 7 sein.

b  Er hat das Autoprotolyse-­Gleichgewicht des Wassers nicht be­rücksichtigt. Die Konzentration der Oxonium­-Ionen aus der Auto­protolyse des Wassers ist ca. 100­mal größer als die Konzentration der Oxonium-­Ionen durch die Protolyse von HCl. Der pH­-Wert der Lösung liegt in guter Näherung bei 7.

 

Aufgabe 12

In „hartem“ Wasser liegen gelöste Ca²⁺­ und HCO₃⁻­Ionen vor.
Calciumhydroxid bildet bei der Dissoziation in wässriger Lösung Ca²⁺­ und OH⁻­Ionen.

 

Aufgabe 13

a pH = 11 ⇨ pOH = 3 ⇨ c(OH⁻) = 10⁻³ mol l⁻¹
pH = 3 ⇨ c(H₃O⁺) = 10⁻³ mol · l⁻¹
OH⁻ + H₃O⁺ ⟶ 2 H₂O

b Die Stoffmenge der Oxonium-Ionen in 1 l Salzsäure ist gleich der Stoffmenge der Hydroxid­-Ionen in 1 l Natronlauge bzw. Ammoniaklösung.

Die Natronlauge wurde genau neutralisiert, der pH­-Wert beträgt 7. In der Ammoniaklösung mit pH = 11 liegt zusätzlich folgendes Gleichgewicht vor: NH₃ + H₂O  \( \rightleftharpoons\) OH⁻ + NH₄⁺ 

c(NH₃) beträgt dabei ein Mehrfaches von c(OH ), weil NH₃ nur eine mittelstarke Base ist:
K_B(NH₃) = 10^−pKB = 1,78 · 10⁻⁵ mol · l⁻¹

\( K_{\rm B}{\rm (NH_3)} = \frac {c{\rm (OH^-})\ ·\ c{\rm (NH_4^+)}} {c{\rm (NH_3)}} \) bzw.

\( c{\rm (NH_3)} = \frac {c{\rm (OH^-})\ ·\ c{\rm (NH_4^+)}} {K_{\rm B}{\rm (NH_3)} } \)

Unter der Annahme, dass c(NH₄⁺) = c(OH⁻) ist, folgt: c(NH₃) = 0,056 mol · l⁻¹

Werden alle Hydroxid-­Ionen aus dem Gleichgewicht entfernt, so stellt es sich nach dem Prinzip von Le Chatelier neu ein, indem NH₃ mit H₂O reagiert und wieder OH⁻­-Ionen erzeugt werden. Die Lösung bleibt auch nach Zugabe der Salzsäure alkalisch.

 

Aufgabe 14

a Der Essigsäure-­Acetat-­Puffer (pK_S= 4,75) ist geeignet, da der pK_S­-Wert dicht an pH = 5,0 liegt:
HA = CH₃COOH und A⁻ = CH₃COO⁻

b

pH = pK_S + lg \( \frac {c{\rm (A^-)}} {c{\rm (HA)}} \)

pH − pK = 0,25 = lg \( \frac {c{\rm (A^-)}} {c{\rm (HA)}} \)

10^0,25 = \( \frac {c{\rm (A^-)}} {c{\rm (HA)}} \) ≈ 1,78

 

Aufgabe 15

a H₃O⁺ + CH₃COO⁻ ⟶ CH₃COOH + H₂O

b Die Pufferkapazität ist die Stoffmenge an Oxonium-­Ionen, die den pH­-Wert eines Puffers um eine Einheit senkt. Deshalb werden im Folgenden Stoffmengen betrachtet.

n₀(HA) = c₀(HA) · V(Puffer) = 0,25 mol n₀(A⁻) = c₀(A⁻) · V(Puffer) = 0,25 mol Wegen n₀(HA) = n₀(A⁻) gilt:

pH = pK_S + lg \( \frac {n_0{\rm (A^-)}} {n_0{\rm (HA)}} \) = 4,75

Durch die Reaktion (⇒ Teilaufgabe a) entstehen aus x Acetat­ Ionen mit x Oxonium-­Ionen x Essigsäuremoleküle, d. h., es gilt:

pH = pK_S + lg \( \frac {(n_0{\rm (A^-)}\ -\ x)} {(n_0{\rm (HA)} \ +\ x)} \) = 3,75

pH – pK_S = -1 = lg \( \frac {(n_0{\rm (A^-)}\ -\ x)} {(n_0{\rm (HA)}\ +\ x)} \)

⇒ 10⁻¹ = 0,1 = \( \frac {(n_0{\rm (A^-)}\ -\ x)} {(n_0{\rm (HA)}\ +\ x)} \)

⇒ x = n(H₃O⁺) = \( \frac {(n_0{\rm (A^-)}\ -\ 0,1\ ·\ (n_0{\rm (HA)})} {1,1} ≈ 0,205 mol

Die Pufferkapazität beträgt 0,205 mol H₃O⁺.

c pH = pK_S +  \( \frac {c{\rm (A^-)}} {c{\rm (HA)}} \) = 4,75

Zur Berechnung des pH-Wertes nach Zugabe der Salzsäure werden Stoffmengen betrachtet:

n₀(HA) = c₀(HA) · V(Puffer) = 0,25 mol n₀(A⁻) = c₀(A⁻) · V(Puffer) = 0,25 mol n(H₃O⁺) = c(H₃O⁺) · V(Salzsäure) = 0,1 mol

0,1 mol H₃O⁺ reagieren mit 0,1 mol CH₃COO⁻ zu 0,1 mol CH₃COOH.

⇒ n(HA) = n₀(HA) + 0,1 mol = 0,35 mol
⇒ n(A⁻) = n₀(A⁻) − 0,1 mol = 0,15 mol

pH = pK_S + lg \( \frac {n{\rm (A^-)}} {n{\rm (HA)}} \) ≈ 4,38

d Zur Berechnung des Volumens der Salzsäure werden Stoff­ mengen betrachtet:

n₀(HA) = c₀(HA) · V(Puffer) = 0,25 mol

n₀(A⁻) = c₀(A⁻) · V(Puffer) = 0,25 mol

V(Salzsäure) =  \( \frac {n{\rm (H_3O^+)}} {c{\rm (H_3O^+)}}  = \frac {x} {c{\rm (H_3O^+)}} \)

Durch die Reaktion (⇒ Teilaufgabe a) entstehen aus x Acetat­Ionen mit x Oxonium­-Ionen x Essigsäuremoleküle, d. h., es gilt:

pH = pK_S + lg \( \frac {(n_0{\rm (A^-)}\ -\ x)} {(n_0{\rm (HA)}\ +\ x)} \)

pH – pK_S = -0,75 = lg \( \frac {(n_0{\rm (A^-)}\ -\ x)} {(n_0{\rm (HA)}\ +\ x)} \)

⇒ 10^{−0,75 ≈} 0,178 = \( \frac {(n_0{\rm (A^-)}\ -\ x)} {(n_0{\rm (HA)}\ +\ x)} \)

⇒ x = \( \frac {(n_0{\rm (A^-)}\ -\ 0,178\ ·\ (n_0{\rm (HA)})} {1,178} \) ≈ 0,174 mol

V(Salzsäure) = \( \frac {x} {x{\rm H_3O^+)}} \) = 0,174 l

 

Aufgabe 16

a H₃PO⁴ + OH⁻ ⟶ H₂O + H₂PO₄⁻
H₂PO₄⁻ + OH⁻  ⟶ H₂O + HPO₄²⁻
HPO₄²⁻ + OH⁻ ⟶ H₂O + PO₄³⁻

b  Geg.: V(Natronlauge) = 0,01 l, c(OH⁻) = 0,1 mol · l⁻¹ , M(H₃PO₄) = 100 g · mol⁻¹; ges.: n(H₃PO₄), m(Phosphorsäure)

Der Umschlagbereich von Phenolphthalein fällt in den pH­-Sprung beim 2. Äquivalenzpunkt der Titrationskurve von Phosphor­säure, d. h., bis zu diesem Punkt sind die beiden ersten Reaktionen (⇒ Teilaufgabe a) abgelaufen. Zusammengefasst:

H₃PO₄ + 2 OH⁻ ⟶ 2 H₂O + HPO₄²⁻

D.h., n(H₃PO₄) = \( \frac {1}{2} \)  n(OH⁻)

n(OH⁻) = V(Natronlauge) · c(OH⁻) = 0,001 mol
n(H₃PO₄) = 0,0005 mol
m(Phosphorsäure) = n(H₃PO₄) · M(H₃PO₄) = 0,1 g

 

Aufgabe 17

a Reaktionsgleichung: NH₃ + H₃O⁺ ⟶ H₂O + NH₄⁺

0 ml Salzsäure: Es liegt eine Ammoniaklösung vor, Berechnung des pH-­Werts nach der Gleichung für mittelstarke Basen:

1 ml, 5 ml, 9 ml Salzsäure: Es liegen Ammonium-­Ammoniak­ Puffer­-Lösungen vor, Berechnung des pH­-Werts mit der Puffer­gleichung.

10 ml: 1. Äquivalenzpunkt: Es liegt eine Lösung von Ammonium­chlorid vor, Berechnung des pH­-Werts nach der Gleichung für mittelstarke Säuren:

11 ml: Es liegt die Lösung einer sehr starken Säure (H₃O⁺) vor.

 

V in ml	c(NH3) in mol · l−1	c(NH4+) in mol · l−1	pH
0	0,1	0	11,12
1	0,09	0,01	10,21
5	0,05	0,05	9,25
9	0,01	0,09	8,29
10	0	0,1	5,13
11	0	0	2

 

b

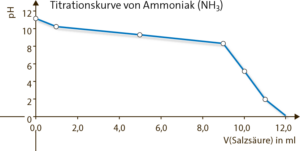
c Der pH-Sprung umfasst die Umschlagbereiche von Methylrot und Bromkresolgrün.

____________________________________________________

Seite 70

pH-Wert der Lösung einer schwachen Säure

Aufgabe 1

a

 

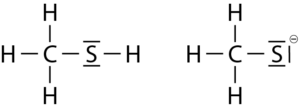
b Die Bindung zwischen dem Sauerstoff- und dem Wasserstoffatom im Methanolmolekül ist aufgrund der größeren Differenz der Elektrongativität (ΔEN = 1,3) stärker polar als die Bindung zwischen dem Schwefel- und dem Wasserstoffatom im Methanthiolmolekül (ΔEN = 0,4). Das Sauerstoffatom trägt somit eine größere negative Teilladung als das Dadurch sind Wasserstoffbrücken zwischen Methanolmolekülen stärker als zwischen Methanthiolmolekülen. Es wird mehr Energie benötigt, um erstere zu lösen, sodass die Siedetemperatur für Methanol höher liegt als die für Methanthiol.

c CH₃SH hat den kleineren pK_S-Wert (10,4 vs 15,5) und ist damit die stärkere Säure.

 

Aufgabe 2

(i) Da es sich bei der Protolyse von CH₃SH-Molekülen mit H2O-Molekülen um eine endotherme Reaktion
handelt, wird das Protolysegleichgewicht bei Senkung der Temperatur nach dem Prinzip von Le Chatelier
auf die Seite der Edukte verschoben. Dabei werden Oxonium-Ionen verbraucht, ihre Konzentration sinkt und
der pH-Wert steigt.

(ii) Eine Erhöhung der Konzentration der Thiolat-Ionen stört das Protolysegleichgewicht. Nach dem Prinzip
von Le Chatelier wird die Reaktion beschleunigt, bei der die Thiolat-Ionen verbraucht und ihre Konzentration
gesenkt wird. Dadurch werden auch Oxonium-Ionen verbraucht, ihre Konzentration sinkt und der pH-Wert
steigt.

(iii) Die CH₃S^–-Ionen reagieren in einer Gleichgewichtsreaktion mit den Zn²⁺-Ionen zu Zn(CH₃S)⁺-Ionen.
Durch die Einstellung des chemischen Gleichgewichts verringert sich die Konzentration der CH₃S^–-Ionen.
Als Konsequenz ist das Protolysegleichgewicht des Methanthiols gestört, weil die Reaktion zwischen
CH₃S^–-Ionen und H₃O⁺-Ionen verlangsamt wurde. Nach dem Prinzip von Le Chatelier werden nun vermehrt
CH₃S^–-Ionen und damit auch H₃O⁺-Ionen gebildet. Somit nimmt c(H₃O⁺) zu und der pH-Wert sinkt.

 

____________________________________________________

Seite 71

linke Spalte: Gefahr beim Verzehr von Lakritzwaren?

Aufgabe 1

pK_S (NH₄⁺) =9,25 ⇒ schwache Säure

pK_B (Cl^–) = 2,1 ⇒ sehr schwache Base

Da der pK_s-Wert deutlich kleiner ist als der pK_B-Wert, reagiert die Lösung sauer.

Aufgabe 2

NH₄⁺ + H₂O \( \rightleftharpoons\)  NH₃ + H₃O⁺

Säure1 + Base2  \( \rightleftharpoons\)  Base1 + Säure2

Das Gleichgewicht liegt auf der linken Seite.

Aufgabe 3

a c= n/V
n= m/M
M(NH₄⁺) = 18,04 g ∙ mol⁻¹

n(NH₄⁺) =  \( \frac {1\ g}{18,04\ g\ ·\ mol^{-1}} \) = 0,055 mol

c(NH₄⁺) = \( \frac {0,055\ mol}{0,4\ l} \) =  0,1375 mol ∙ l⁻¹

pK_S(NH₄⁺) = 9,25 ⇒ pH= 0,5∙[pK_S(HA) – lg(c₀(HA))]

pH= 0,5 ∙ [9,25 – lg(0,1375) = 5,06

Die Lösung ist schwach sauer und der pH-Wert vergleichbar mit denen von Gurken (pH  ≈  5,4) oder Blumenkohl (pH  ≈  5,6).

b pH = 4,56; vereinfacht: c₀(HA) = 10^{pKs(HA) – 2 pH}

c₀(NH₄⁺) = 10^{9,25 – 2 ∙ 4,56} = 1,35 mol ∙ l⁻¹

Es gilt vereinfacht: c₀(NH₄⁺) = c(NH₄Cl)
M(NH₄Cl) = 53,4 g ∙ mol⁻¹

c(NH₄Cl) = ω ∙ \( \frac {ρ\ (Sirup)}{M(NH_4Cl)} \) ⇔ ω = \( \frac {c(NH_4Cl)\ ·\ M(NH_4Cl)}{ρ\ (Sirup)} \) ∙ 100%

ω = \( \frac {1,35\ mol\ ·\ l^{-1}\ ·\ 53,4\ g\ ·\ mol^{-1}}{1400\ g\ ·\ l^{-1}} \) ∙ 100%= 5,16 %

Der Lakritzsirup fällt in die Kategorie „extra stark“ und ist damit für Kinder nicht geeignet.

rechte Spalte: Ascorbinsäure in Lebensmitteln

Aufgabe 1

a H₂Asc + H₂O \( \rightleftharpoons\) HAsc^– + H₃O⁺

HAsc^– + H₂O \( \rightleftharpoons\) Asc^2– + H₃O⁺

b Brönstedt-Säure: Ein Teilchen reagiert als Brönstedt-Säure, wenn es ein Proton abgibt (Protonendonator).

Brönstedt-Base: Ein Teilchen reagiert als Brönstedt-Base, wenn es ein Proton aufnimmt (Protonenakzeptor).

H₂Asc + H₂O \( \rightleftharpoons\) HAsc^– + H₃O⁺

Säure 1 + Base 2 \( \rightleftharpoons\) Base 1 + Säure 2

H₂Asc gibt ein Proton ab, ist Protonendonator und damit Brönstedt-Säure.

H₂O nimmt ein Proton auf, ist Protonenakzeptor und damit Brönstedt-Base.

c  Es handelt sich um Protolysegleichgewichte, die durch die Anzahl der Oxoniumionen beeinflusst werden, da diese Bestandteil der Gleichgewichte sind. Wenn die Anzahl der Oxoniumionen zunimmt, weil der pH-Wert erniedrigt wird, verschiebt sich das Gleichgewicht in die Richtung der Edukte.

Aufgabe 2

pK_S(H₂Asc) = 4,2 ⇒ schwache Säure

c₀(HA) = 10^{pKs(HA) – 2 pH}

c₀(H₂Asc)  = 10^{4,2 – 2 ∙ 3,1}  = 0,01 mol ∙ l⁻¹

Aufgabe 3

Annahme: ρ (Saft) = 1 g · ml⁻¹

m = M ∙ n; M(H₂Asc) = 176,124 g ∙ mol⁻¹

m = 176,124 g ∙ mol⁻¹ ∙ 0,00086 mol = 0,15 g = 150 mg

\( \frac {150\ mg}{100\ g} \) = \( \frac {105\ mg}{m(Saft)} \) ⇔ m(Saft)= \( \frac {100\ ml}{150\ g} \) ∙ 105 mg = 70 g ≙ 70 ml

Die Schwangere muss 70 ml Saft trinken, um ihren Tagesbedarf an Vitamin C zu decken.

____________________________________________________

Seite 72

Vanillin – die geschmacksbildende Säure im Vanillin-Zucker

Aufgabe 1

Das Vanillinmolekül ist der Protonendonator: Die elektronenziehende Aldehydgruppe des Vanillinmoleküls erhöht durch ihren −M-Effekt die Acidität an der phenolischen OH-Gruppe. Bei der Säure-Base-Reaktion zwischen Vanillin und Wasser wird das Wasserstoffatom der phenolischen OH-Gruppe abgespalten und auf das Wassermolekül, den Protonenakzeptor, übertragen. Als Reaktionsprodukt entstehen das Vanillin-Anion und ein Oxonium-Ion.

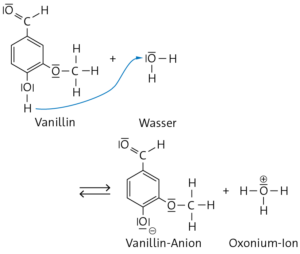
Aufgabe 2

n(HA) = \( \frac {m(HA)}{M(HA)} \)

n(Vanillin) = \( \frac {1,52\ g}{52,15\ g\ ·\ mol^{-1}} \) = 0,029 mol

c₀(HA) = \( \frac {n(HA)}{V} \)

c₀(Vanillin) = \( \frac {0,029\ mol}{100\ ml} \) = 0,29 mol · l⁻¹

pH = 0,5 · (pK_S − lg c₀); pK_S = 7,4

pH = 0,5 · (7,4 − lg 0,29) = 3,97

Aufgabe 3

Man titriert die unbekannte Lösung mit einer starken Base und zeichnet eine Titrationskurve. Da es eine schwache Säure ist, gibt es einen Halbäquivalentpunkt. Dieser kann grafisch bestimmt werden und entspricht dem pK_s-Wert.

Mithilfe des so ermittelten pK_s-Wertes und dem zu Beginn der Titration gemessenen pH-Wert kann nun die Anfangskonzentration der schwachen Säure berechnet werden. Es gilt:

pH = 0,5 · (pK_S − lg c₀)
⇔ 2 pH = [pK_s – lg c₀]
⇔ 2 pH – pK_s =  – lg c₀
⇔ – [2 pH – pK_s] = lg c₀
⇔ c₀ = 10^-(2pH-pKs) = 10^pKs-2pH

Aufgabe 4

pH = – lg c(H₃O⁺)  = 0,5 · (pK_S − lg c₀)
– lg c(H₃O⁺)  = 0,5 · (7,4 − lg 0,25) = 4
⇔ c(H₃O⁺) = 10^-4 = 0,0001 mol ∙ l^–1

Die Konzentration des Vanillin-Anions ist genauso groß wie die der Oxonium-Ionen.

c(H₃O⁺) = c(A^–) = 0,0001 mol ∙ l^–1
c(HA)     = 0,2499 mol ∙ l^–1

Aufgabe 5

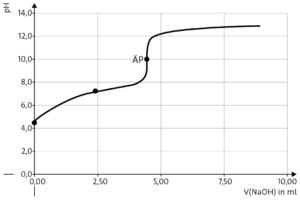
Erläuterung der Titrationskurve: Es handelt sich um das Ergebnis der Titration einer schwachen Säure mit einer starken Base, da die Kurve gleich zu Beginn bei Zugabe von 1 ml Natronlauge zunächst kurz stark ansteigt, dann bis zu einer Zugabe von ca. 7,5 ml leicht ansteigt, bevor es zu einem großen pH-Sprung kommt. Der Äquivalenz-punkt der Titration wird nach Zugabe von ca. 8,5 ml der Natronlauge erreicht. Hier liegt ein pH-Wert von ca. 10 vor, der also deutlich im alkalischen Bereich liegt. Am Äquivalenzpunkt liegt die korrespondierende Base der Säure Vanillin vor; in einer Protolysereaktion mit Wasser bilden sich Vanillin-Moleküle und Hydroxidionen, die zu dem alkalischen pH-Wert führen.

Berechnung der extrahierten Stoffmenge in der Ausgangs-lösung:
Am Äquivalenzpunkt gilt n(Vanillin) = n(OH^–)
n(OH^–) = c(Natronlauge) · V(Natronlauge)
n(OH^–) = 0,1 mol ∙ l^–1 · 0,0085 l = 8,5 · 10^–4 mol

Mögliche Fehlerquellen: Bei dem beschriebenen Verfahren können Fehler an verschiedenen Stellen auftreten, etwa:

• Keine 100%ige Überführung des Vanillinzuckers aus dem Päckchen oder Inhalt des Päckchens beträgt nicht genau 10 g
• Flüssigkeitsverlust beim Dekantieren
• Ungenaue pH-Wert-Messung, mehr Messpunkte am Anfang der Kurve wären sinnvoll
• Ungenaues Ablesen des zugegebenen Volumens Natronlauge am Äquivalenzpunkt

Aufgabe 6

Da der Äquivalentpunkt der Titration bei ca. pH 10 liegt, eignet sich ein Indikator, der dort seinen Umschlags-bereich hat, also etwa Thymolphthalein.

Aufgabe 7

Vor Zugabe der Maßlösung: pH = 0,5 · (pK_S − lg c₀)
pH = 0,5 · (7,4 − lg 0,1) = 4,2
⇒ Punkt: (V = 0 ml / pH = 4,2)

Am Äquivalenzpunkt: n(Vanillin) = n(OH^–); pH=10
n(OH^–) = 8,5 · 10^–5 mol (aus Aufgabe 5)

V (KOH) = \( \frac {n(OH^-)}{c(KOH)} \) = \( \frac {n(8,5\ ·\ 10^{-4} mol)}{0,2\ mol\ ·\ l} \) = 4,25 ml

⇒ Punkt: (V=4,25 ml / pH=10)

Am Halbäquivalenzpunkt gilt nach der Hendersson-Hasselbach-Gleichung c(HA)= c(A⁻) und damit  pH = pK_S
⇒ am Halbäquivalenzpunkt ist pH = 7,4

Die Kurve nähert sich pH ≈ 12,5 an (Seite 72, Abbildung 1)

________________________________________________________

Seite 73

linke Spalte: Die clevere Assistentin

Aufgabe 1

a Gegeben: HA = CH₃COOH; B = CH₃COO⁻
n(CH₃COOH) = 0,5 mol
n(CH₃COO⁻) = 0,5 mol; V = 1 l
pK_S(CH₃COOH) = 4,75

Gesucht: pH-Wert
pH = pK_S (CH₃COOH) + lg [ \( {\rm \frac {c (CH_3COO^-)}{c(CH_3COOH)} } \) ]
c(CH₃COOH) = \( {\rm \frac {n (CH_3COOH)}{V} } \) = 0,5 mol · l⁻¹
c(CH₃COO⁻) = \( {\rm \frac {n (CH_3COO^-)}{V} } \) = 0,5 mol · l⁻¹
pH = 4,75

b  Der pH-Wert bleibt gleich, weil die Konzentrationen der Säure HA und der Base B um den gleichen Faktor verringert werden.

Die Pufferkapazität ist die Stoffmenge an Oxonium-Ionen, die notwendig ist, um den pH-Wert um 1 zu senken. Wird die Pufferkonzentration um einen Faktor 10 verringert wird, so sinkt auf die Pufferkapazität um den gleichen Faktor.

Aufgabe 2

a Acetat-Ionen, CH₃COO⁻, entstehen bei der Reaktion von Essigsäure, CH₃COOH, mit Natronlauge.
CH₃COOH + OH⁻ → H₂O + CH₃COO^−#

b 0,5 Liter der Essigsäurelösung (c = 2,0 mol ∙ l⁻¹) ent- halten n = c ∙ V = 1,0 mol Essigsäuremoleküle. Werden davon 0,5 mol in Acetat-Ionen umgewandelt, liegen noch 0,5 mol Essigsäuremoleküle vor.

Zur Umwandlung werden n = 0,5 mol Natriumhydroxid benötigt. Das sind m = n ∙ M = 20,0 g Natriumhydroxid. Abschließend füllt man die Lösung noch mit Wasser auf 1,0 Liter auf.

c 60 g Essigsäure entsprechen n = m/M = 1 mol Essig- säuremoleküle. Werden davon 0,5 mol in Acetat-Ionen umgewandelt, liegen noch 0,5 mol Essigsäuremoleküle vor. Zur Umwandlung werden n = 0,5 mol Hydroxid-Ionen benötigt. Das sind V = n/c = 0,5 l der Natronlauge. Ab- schließend füllt man die Lösung noch mit Wasser auf 1,0 Liter auf.

Aufgabe 3

a Oxonium-Ionen (H₃O⁺) reagieren als Säure mit der Base des Puffers, CH₃COO⁻.
H₃O⁺ + CH₃COO⁻ → CH₃COOH + H₂O

b Gegeben: n(H₃O⁺) = 0,1 mol; pK_S(CH₃COOH) = 4,75
Gesucht: pH-Wert
Durch die Reaktion der Oxonium-Ionen werden 0,1 mol Acetat-Ionen in 0,1 mol Essigsäuremoleküle umgewandelt.
n(CH₃COOH) = 0,6 mol; n(CH₃COO⁻) = 0,4 mol.

Statt der entsprechenden Konzentrationen können wegen der Gleichung c = n/V auch die Stoffmengen von Puffersäure und -base in die Puffergleichung eingesetzt werden.

pH = pK_S (CH₃COOH) + lg [ \( {\rm \frac {n (CH_3COO^-)}{n(CH_3COOH)} } \) ]
pH ≅ 4,57.

rechte Spalte: Puffer in der Analytik

Aufgabe 1

a Für die Bestimmung der Wasserhärte muss die Reaktion
M²⁺ + H₄EDTA + 4 H₂O \( \rightleftharpoons \) [MEDTA]²⁻ + 4 H₃O⁺

vollständig verlaufen, d. h., das Gleichgewicht muss auf die rechte Seite verschoben werden. Das gelingt, indem die entstehenden Oxonium-Ionen durch Reaktion mit einer Pufferbase B abgefangen werden.

b Ein hoher pH-Wert bedeutet eine hohe Konzentration von Hydroxid-Ionen. Ein hoher pH-Wert begünstigt die Bildung von schwerlöslichen Metallhydroxiden, M(OH)₂. Dadurch werden die M²⁺-Ionen aus der Lösung entfernt und können nicht mehr mit H4EDTA reagieren. Die gefundenen Konzentrationen von M²⁺ sind dann zu klein.

Aufgabe 2

a H₃O⁺ + NH₃ → NH₄⁺ + H₂O
OH⁻ + NH₄+ → NH₃ + H₂O

b pH = pK_S (NH₄⁺) + lg [ \( {\rm \frac {c (NH_3)}{c(NH_4^+)} } \) ]

c Bei gleichen Stoffmengen n₀ bzw. gleichen Konzentrationen c₀ gilt:

pH = pK_S (NH₄⁺) + lg [ \( {\rm \frac {c_0}{c_0} } \) ]

Wenn 10 % der NH₃-Moleküle mit H₃O⁺-Ionen zu NH₄⁺– Ionen reagieren, nimmt die Stoffmenge der NH₃-Moleküle von c₀ auf 0,9 ∙ c₀ ab und die der NH₄⁺-Ionen von c₀ auf 1,1 ∙ c₀ zu.

pH = pK_S (NH₄⁺) + lg [ \( {\rm \frac {0,9\ ·\ c_0}{1,1\ ·\ c_0} } \) ]

Für die Änderung, ΔpH, gilt:

ΔpH = lg ( \( \frac {0,9}{1,1} \) ) = -0,09

Der pH-Wert sinkt also um 0,09.

d Gegeben: ΔpH = −0,1
Gesucht: N = c₀(NH₃)/c₀(M²⁺)

Für jedes M²⁺-Ion, das mit H₄EDTA reagiert, entstehen 4 H₃O⁺-Ionen, die mit 4 NH₃-Molekülen zu 4 NH₄⁺-Ionen reagieren. Die Zahl der NH₃-Moleküle sinkt von N auf (N − 4), die Konzentration von NH₄⁺ steigt von N auf (N + 4).

Für die pH-Wert-Änderung gilt:

ΔpH = lg [ \(  {\rm \frac {N\ -\ 4}{N\ +\ 4}} \) ] – lg \( {\rm \frac {N}{N}} \)

0,1 = lg [ \(  {\rm \frac {N\ -\ 4}{N\ +\ 4}} \) ]

10^−0,1 =  \(  {\rm \frac {N\ -\ 4}{N\ +\ 4}} \)

N = \( \frac {4\ +\ 4\ ·\ 10^{-0,1}} {1\ -\ 10^{-0,1}} \) ≅ 34,9

c₀(NH₃) muss mindestens 34,9-mal so groß sein wie c₀(M²⁺).

 

 

 

© Cornelsen Verlag GmbH