Chemie 1. Energetik Lösungen – Cornelsen

Lösungen Check-up

Seite 47

Aufgabe 1:

Gegeben: m(Marshmallow) = 1,5 g; m(H₂O) = 410 g; ΔT = 11,9 K; c_p(H₂O) = 4,18 J · g⁻¹ · K⁻¹

Gesucht: Q

Lösung: Q = – c_p(H₂O) · m(H₂O) · ΔT

Q = – 4,18 J · g⁻¹ · K⁻¹ · 410 g · 11,9 K

Q = – 20 394 J = – 20,39 kJ

Antwort: Bei der Verbrennung von 1,5 g Marshmallows wurde eine Reaktionswärme Q = -20,39 kJ freigesetzt.

Aufgabe 2:

1. Berechnen von $ Δ_r H$ (entspricht Q):

$$\mathrm{\Delta_r}H\ =\ -\ c\mathrm{_p(H_2 O)}\ · [m{\rm (H_2 O)} + m{\rm (Lösung)] · ΔT}$$

$${\rm =\ -\ 4,18\ J\ · g^{-1} · K^{-1} · 325\ g · 5,2}$$

$${\rm =\ -7064\ J =\ -7,06\ kJ}$$

2. Berechnen der umgesetzten Stoffmenge Wasserstoffperoxid:

$$n\mathrm{(H_2 O_2)}\ =\ c\mathrm{(H_2 O_2)}\ · V = 1\ {\rm mol · l^{-1} · 0,075 l}$$

$$=\ 0,075\ {\rm mol}$$

3. Berechnen der molaren Reaktionsenthalpie:

$$\mathrm{\Delta_r}H_{\rm m}\mathrm{(H_2 O_2)}\ = \frac{\mathrm{\Delta_r}H}{n\mathrm{(H_2 O_2)}} = \frac{-7,06 {\rm \ kJ}}{0,075\ {\rm mol}}$$

$$ {\rm =\ -94,1\ kJ · mol^{-1}}$$

Nach der Definition bezieht sich die berechnete molare Reaktionsenthalpie auf die Umsetzung von 1 mol Wasserstoffperoxid pro 1 mol Formelumsatz.
In der Reaktionsgleichung werden aber 2 mol Wasserstoffperoxid pro 1 mol Formelumsatz umgesetzt, sodass nach obiger Reaktionsgleichung die doppelte Menge an Reaktionsenthalpie frei wird.

Antwort:

$ {\rm 2\ H_2 O_2 (l)} \rightarrow {\rm 2\ H_2 O (l) +\ O_2 (g)} $

$ \mathrm{\Delta_r}H_{\rm m} =\ -188,4\ {\rm kJ · mol^{-1}} $

Aufgabe 3:

1. Berechnen von $ H_{\rm s}$ aus $Δ_{\rm c} H_{\rm m} {\rm (C_6 H_6):}$

$$H_S = \frac {-\mathrm{\Delta_c}H_{\rm m} {\rm (C_6 H_6)}}{M {\rm(C_6 H_6)}} = {\rm \frac {3268\ kJ · mol^{-1}}{78\ g · mol^{-1}}} = {\rm 41,9\ kJ · g^{-1}}$$

2. Berechnen von Hi:

$$C_6 H_6 (l) + \frac {15}{2} O_2 (g) \rightarrow 6 CO_2(g) + 3 H_2 O (g)$$

Berechnen der Reaktionsenthalpie mit gasförmigem Wasser:

$$\mathrm{\Delta_c}H_{\rm m} {\rm(C_6 H_6)} + 3 · \mathrm{\Delta_v}H_{\rm m} {\rm (H_2 O)}$$

$$=\ {\rm -3268\ kJ · mol^{-1} + 3 · 44\ kJ · mol^{-1}}$$

$$=\ {\rm -3136 \ kJ · mol^{-1}}$$

$$H_i =\ \frac {-\mathrm{\Delta_r}H_{\rm m} {\rm (C_6 H_6)}}{M {\rm(C_6 H_6)}} = {\rm \frac {3136\ kJ · mol^{-1}}{78\ g · mol^{-1}}} = {\rm 40,2\ kJ · g^{-1}}$$

Antwort: Für Benzol beträgt der Brennwert $ H_{\rm s}$ = 41,9 kJ/g und der Heizwert $ H_{\rm i}$ = 40,2 kJ/g .

Aufgabe 4:

1. Reaktionsgleichung:

$ {\rm C_6 H_{12} O_6 (s) + 6\ O_2 (g)}\ \rightarrow \ {\rm \color{red}{6}\ CO_2 (g) + \color{blue}{6}\ H_2 O (l)} $

2. Berechnen von $\Delta_c H^{\rm 0}_{\rm m} $ (Edukte):

$ Δ_{\rm r} H^{\rm 0}_{\rm m} = ∑\ ν · Δ_{\rm f} H^{\rm 0}_{\rm m} \ {\rm (Produkte)}\ -\ ∑\ ν · Δ_{\rm f} H^{\rm 0}_{\rm m} \ {\rm (Edukte)} $

Hinweis: Die Standardbildungsenthalpien der Elemente sind per Definition null und müssen nicht berücksichtigt werden. Deshalb geht Sauerstoff nicht in die Berechnung ein.
$$ Δ_{\rm c} H^{\rm 0}_{\rm m}\ {\rm (C_6 H_{12} O_6)} = \color{red}{6} · Δ_{\rm f} H^{\rm 0}_{\rm m} {\rm (CO_2)} + \color{blue}{6} · Δ_{\rm f} H^{\rm 0}_{\rm m} {\rm (H_2 O)}\ – 6 · Δ_{\rm f} H^{\rm 0}_{\rm m} {\rm (C_6 H_{12} O_6)}\ $$

$$ = \color{red}{6} · (-394\ {\rm kJ · mol^{-1}}) + \color{blue}{6} · (-286\ {\rm kJ · mol^{-1}})\ – ( -1274\ {\rm kJ · mol^{-1}}) $$

$$ = -2806\ {\rm kJ · mol^{-1}}$$

Antwort: Die molare Standardverbrennungsenthalpie von fester Glucose beträgt -2806 kJ/mol.

Aufgabe 5:

1. Reaktionsgleichung:

$ {\rm C_6 H_6 (l) + \frac{15}{2} O_2 (g)} \rightarrow \color{red}{6} \ {\rm CO_2 (g) + \color{blue}{3} \ H_2 O (l)} $

2. Berechnen von $ Δ_{\rm f} H^{\rm 0}_{\rm m} {\rm (C_6 H_6)}: $

$ Δ_{\rm r} H^{\rm 0}_{\rm m} = ∑\ ν · Δ_{\rm f} H^{\rm 0}_{\rm m} \ {\rm (Produkte)}\ -\ ∑\ ν · Δ_{\rm f} H^{\rm 0}_{\rm m} \ {\rm (Edukte)} $

$ Δ_{\rm c} H^{\rm 0}_{\rm m} {\rm (C_6 H_6)} = \color{red}{6} · Δ_{\rm f} H^{\rm 0}_{\rm m} {\rm (CO_2)} + \color{blue}{3} · Δ_{\rm f} H^{\rm 0}_{\rm m} {\rm (H_2 O)}\ -\ Δ_{\rm f} H^{\rm 0}_{\rm m} {\rm (C_6 H_6)} $

$ Δ_{\rm f} H^{\rm 0}_{\rm m} {\rm (C_6 H_6)} = \color{red}{6} · Δ_{\rm f} H^{\rm 0}_{\rm m} {\rm (CO_2)} + \color{blue}{3} · Δ_{\rm f} H^{\rm 0}_{\rm m} {\rm (H_2 O)}\ -\ Δ_{\rm c} H^{\rm 0}_{\rm m} {\rm (C_6 H_6)} $

$ = \color{red}{6} · (-394 {\rm kJ · mol^{-1}}) + \color{blue}{3} · (-286 {\rm kJ · mol^{-1}}) -\ (-3268 {\rm kJ · mol^{-1}}) $

$ = (46 {\rm kJ · mol^{-1}}) $

Antwort: Die molare Standardbildungsenthalpie von flüssigem Benzol beträgt 46 kJ/mol.

Aufgabe 6:

Die Reaktionsentropie erfasst nur die Entropieänderung aufgrund der Umgruppierung der Teilchen. Bei einer exothermen Reaktion kann die Reaktionsentropie negativ sein. Durch die freigesetzte Wärme kann die Entropie des isolierten Systems dennoch steigen.

_____________________________________________________________________________________________

Seite 48

Aufgabe 7:

a $ {\rm 2\ Na(s) + 2\ H_2 O(l)} \rightarrow 2\ {\rm NaOH(aq) + H_2(g)} $
$ Δ_{\rm r} H_{\rm m} = 2 · Q = −368\ {\rm kJ · mol^{-1}} $

b Aus 1 mol Natrium entstehen 0,5 mol gasförmiger Wasserstoff. Das sind 12,25 l.
W = − p · ΔV = − 101 300 N · ${\rm m^{−2}}$ · (0,01225 m³ − 0 m³) ≈ 1241 N · m² = 1,241 kJ

Aufgabe 8:

$ Q_{\rm g} = Q + Δ_{\rm v} H $
$ Q = m({\rm H_2O}) · c_{\rm p} {\rm (H_2O) · ΔT} = {\rm 500\ g · 4,18\ J · g^{-1} · K^{-1} · 75\ K} = 156,75\ {\rm kJ}$

$ Δ_{\rm v}H = Δ_{\rm v}H_{\rm m} · n({\rm H_2O}) = Δ_{\rm v}H_{\rm m} · \frac {m({\rm H_2O})}{M({\rm H_2O})} $

$ = 44\ {\rm kJ · mol^{-1}} · \frac {500\ {\rm g}}{18\ {\rm g · mol^{-1}}} = 1222,22\ {\rm kJ} $

$ Q_{\rm g}$ = 156,75 kJ + 1222,22 kJ = 1378,97 kJ

Aufgabe 9:

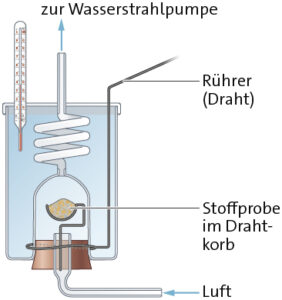
b $ {\rm C_3H_7O_2N(s)} + \frac{15}{4} {\rm O_2(g)} \rightarrow 3\ {\rm CO_2(g)}\ + \frac{7}{2} {\rm H_2O(g)} + \frac{1}{2} {\rm N_2(g)} $

$ Q = -m({\rm H_2O}) · c_{\rm p} {\rm (H_2O) · ΔT} = -240\ {\rm g · 4,18\ J · g^{-1} · K^{-1} · 3,5\ K} = -3511,2\ {\rm J} $

Molare Reaktionsenthalpie

$ Δ_{\rm r}H_{\rm m} = \frac{Q}{n} = Q · \frac{M({\rm C_3H_7O_2N})}{m({\rm C_3H_7O_2N)}} $

$ = -3511,2\ {\rm J} · \frac{89\ {\rm g · mol}^{-1}}{1\ {\rm g}} $

$ = -312,5\ {\rm kJ · mol^{-1}} $

Molare Verbrennungsenthalpie

$ Δ_{\rm c}H_{\rm m} = Δ_{\rm r}H_{\rm m} -\ 3,5 · Δ_{\rm v}H_{\rm m} = -312,5\ {\rm kJ · mol^{-1}} -\ 3,5 · 44\ {\rm kJ · mol^{-1}} = -466,5 \ {\rm kJ · mol^{-1}} $

c Heizwert $ H_{\rm i} $:
$ H_{\rm i} = \frac {-Q}{m} = \frac {3511,2\ {\rm J}}{1\ {\rm g}} = 3511,2\ {\rm J · g^{-1}} = 3,51\ {\rm kJ · g^{-1}} $

Brennzwert $ H_{\rm s} $:
$ H_{\rm s} = \frac {-Δ_{\rm c}H_{\rm m}}{M} = \frac {466,5\ {\rm kJ · mol^{-1}}}{89\ {\rm g · mol^{-1}}} = 5,2\ {\rm kJ · g^{-1}} $

Aufgabe 10:

a $ {\rm C_2H_4(g) + H_2(g)} \rightarrow {\rm C_2H_6(g)} $
$ {\rm C_2H_6(g) + \frac{7}{2} O_2(g)} \rightarrow {\rm 2\ CO_2(g) + 3\ H_2O(l) } $
$ {\rm C_2H_4(g) + 3\ O_2(g)} \rightarrow {\rm 2\ CO_2(g) + 2\ H_2O(l) } $
$ {\rm H_2(g) + \frac{1}{2} O_2(g)} \rightarrow {\rm H_2O(l) } $

C₂H₄ / H₂⇒ CO₂ / H₂O [ ⇒ Δ_cH_m(C₂H₄) / Δ_cH_m(H₂) ]
CO₂ / H₂O ⇒ C₂H₆ [ ⇒ − Δ_cH_m(C₂H₆) ]
C₂H₄ / H₂⇒ C₂H₆ [ ⇒ Δ_rH_m(Hydrierung) ]

$ Δ_{\rm r}H_{\rm m} {\rm (Hydrierung)}= Δ_{\rm c}H_{\rm m} ({\rm C_2H_4}) + Δ_{\rm c}H_{\rm m} ({\rm H_2}) – Δ_{\rm c}H_{\rm m} ({\rm C_2H_6}) $
$ = − 1409\ {\rm kJ · mol^{-1}}) + (-286\ {\rm kJ · mol^{-1}}) – (-1577\ {\rm kJ · mol^{-1}}) = -138\ {\rm kJ · mol^{-1}} $

Aufgabe 11:

a
$ {\rm NaCl(s)} \rightarrow {\rm Na^+(aq) + Cl^- (aq)} $

$ Δ_{\rm r}H_{\rm m} = Δ_{\rm f}H_{\rm m} {\rm (Na^+)} + Δ_{\rm f}H_{\rm m} {\rm (Cl^-)} – Δ_{\rm f}H_{\rm m} {\rm (NaCl)} = -240 \ {\rm kJ · mol^{-1}} + (-167 \ {\rm kJ · mol^{-1}}) – (-411 \ {\rm kJ · mol^{-1}}) = 4 \ {\rm kJ · mol^{-1}} $

$ {\rm CaCl_2(s)} \rightarrow {\rm Ca^{2+}(aq) + 2\ Cl^- (aq)} $

$ Δ_{\rm r}H_{\rm m} = Δ_{\rm f}H_{\rm m} {\rm (Ca^{2+})} + 2 · Δ_{\rm f}H_{\rm m} {\rm (Cl^-)} – Δ_{\rm f}H_{\rm m} {\rm (CaCl_2)} = -543\ {\rm kJ · mol^{-1}} + 2 · (-167\ {\rm kJ · mol^{-1}}) -(-796\ {\rm kJ · mol^{-1}}) = -81\ {\rm kJ · mol^{-1}} $

b Natriumchlorid:
$ Q = Δ_{\rm r}H = 4\ {\rm kJ · mol^{-1}} · 0,1\ {\rm mol} = 400\ {\rm J} $

$ ΔT = \frac{-Q}{m {\rm (H_2O)} \ ·\ c_{\rm p} {\rm (H_2O)} } =\frac{-400\ {\rm J}}{{\rm 100\ g \ ·\ 4,18\ J \ ·\ g^{-1} \ ·\ K^{-1}}} = -0,96\ {\rm K} $

Calciumchlorid:

$ Q = Δ_{\rm r}H = -81\ {\rm kJ · mol^{-1}} · 0,1\ {\rm mol} = -8100\ {\rm J} $

$ ΔT = \frac{8100\ {\rm J}}{{\rm 100\ g\ ·\ 4,18\ J \ ·\ g^{-1} \ ·\ K^{-1}}} = 19,38\ {\rm K} $

Aufgabe 12:

$ Δ_{\rm r}H_{\rm m} = Δ_{\rm f}H_{\rm m} {\rm (CH_3COOH)} + 2 · Δ_{\rm f}H_{\rm m} {\rm (Ag)} + Δ_{\rm f}H_{\rm m} {\rm (H_2O)} – Δ_{\rm f}H_{\rm m} {\rm (CH_3CHO)} – 2 · Δ_{\rm f}H_{\rm m} {\rm (Ag^+)}- 2 · Δ_{\rm f}H_{\rm m} {\rm (OH^-)} $

$ Δ_{\rm r}H_{\rm m} = -486\ {\rm kJ · mol^{-1}} + (-286\ {\rm kJ · mol^{-1}}) – (-192 \ {\rm kJ · mol^{-1}} + 2 · 106\ {\rm kJ · mol^{-1}} – 2 · 230 \ {\rm kJ · mol^{-1}}) = -562 \ {\rm kJ · mol^{-1}}) $

Aufgabe 13:

a $ {\rm NH_3(g) + H_2O(l)} \rightarrow {\rm NH^+_4 (aq) + OH^-(aq)}$

b $ Δ_{\rm r}H_{\rm m} = Δ_{\rm f}H_{\rm m} {\rm (NH^+_4)} + Δ_{\rm f}H_{\rm m} {\rm (OH^-)} – Δ_{\rm f}H_{\rm m} {\rm (NH_3)} – Δ_{\rm f}H_{\rm m} {\rm (H_2O)}$
$ = -132\ {\rm kJ · mol^{-1}} + (-230\ {\rm kJ · mol^{-1}}) – (-46\ {\rm kJ · mol^{-1}} + (-286 \ {\rm kJ · mol^{-1}})) = -30\ {\rm kJ · mol^{-1}}$

c $ Δ_{\rm r}S_{\rm m} = S_{\rm m}{\rm (NH^+_4)} + S_{\rm m}{\rm (OH^-)} – S_{\rm m}{\rm (NH_3)} – S_{\rm m} {\rm (H_2O)}$
$ = 133\ {\rm J · K^{-1} · mol^{-1}} + (-11\ {\rm J · K^{-1} · mol^{-1}}) – 193\ {\rm J · K^{-1} · mol^{-1}} – 70\ {\rm J · K^{-1} · mol^{-1}} = -161\ {\rm J · K^{-1} · mol^{-1}} $

$ Δ_{\rm r}G_{\rm m} = Δ_{\rm r}H_{\rm m} – T · Δ_{\rm r}S_{\rm m} = -30\ {\rm kJ · mol^{-1}} – 298 {\rm K} · (-0,161 {\rm kJ · K^{-1} · mol^{-1}})
≈ 18\ {\rm kJ · mol^{-1}} $ > 0 ⇒ endergonisch

Hinweis: Obwohl die Reaktion endergonisch ist, läuft sie merklich ab, da es sich um eine Gleichgewichtsreaktion handelt.

Aufgabe 14:

a $ Δ_{\rm r}H_{\rm m} = 2 · Δ_{\rm f}H_{\rm m} {\rm (NaCl)} = -822\ {\rm kJ · mol^{-1}} $
$ Δ_{\rm r}S_{\rm m} = 2 · S_{\rm m}{\rm (NaCl)} – 2 · S_{\rm m}{\rm (Na)} – 2 · S_{\rm m}{\rm (Cl_2)}
= 2 · 72\ {\rm J · K^{-1} · mol^{-1}} – 2 · 51\ {\rm J · K^{-1} · mol^{-1}} – 223\ {\rm J · K^{-1} · mol^{-1}} = -181\ {\rm J · K^{-1} · mol^{-1}} $

b $ Δ_{\rm r}G_{\rm m} = Δ_{\rm r}H_{\rm m} – T · Δ_{\rm r}S_{\rm m}$
$ = -822 \ {\rm kJ · mol^{-1}}- 243\ {\rm K} · (-0,181 {\rm kJ · K^{-1} · mol^{-1}}) $
$ ≈ -778\ {\rm kJ · mol^{-1}} $
< 0 ⇒ exergonisch

___________________________________________________________________________________

Seite 49

Süßstoff Aspartam

Aufgabe 1:

$ {\rm C_{14}H_{18}N_2O_5(s) + 16\ O_2(g)} → 14\ {\rm CO_2(g) + 9\ H_2O(l) + N_2(g)} $

$ Δ_{\rm c}H_{\rm m} = -H_{\rm s} · M {\rm (C_{14}H_{18}N_2O_5)} = -17\ {\rm kJ · g^{-1}} · 294\ {\rm g · mol^{-1}} = -4998\ {\rm kJ · mol^{-1}} $

$ Δ_{\rm c}H_{\rm m} = 14 · Δ_{\rm f}H_{\rm m}^0 {\rm (CO_2)} + 9 · Δ_{\rm f}H_{\rm m}^0 {\rm (H_2O)} – Δ_{\rm f}H_{\rm m}^0 {\rm (C_{14}H_{18}N_2O_5)} $

$ Δ_{\rm f}H_{\rm m}^0 {\rm (C_{14}H_{18}N_2O_5)} = 14 · Δ_{\rm f}H_{\rm m}^0 {\rm (CO_2)} + 9 · Δ_{\rm f}H_{\rm m}^0 {\rm (H_2O)} – Δ_{\rm c}H_{\rm m}$
$= 14 · (-394\ {\rm kJ · mol^{-1}}) + 9 · (-286\ {\rm kJ · mol^{-1}}) – (-4998\ {\rm kJ · mol^{-1}}) = -3092 \ {\rm kJ · mol^{-1}} $

Aufgabe 2:

a $ {\rm C_{12}H_{22}O_{11}(s) + 12\ O_2(g)} \rightarrow {\rm 12\ CO_2(g) + 11\ H_2O(l)} $

b $ Q = -c_{\rm p} {\rm (H_2O)} · m{\rm (H_2O)} · ΔT = -4,18\ {\rm J · g^{-1} · K^{-1}} · 650\ {\rm g} · 11,3\ {\rm K} = -30702,1\ {\rm J} = -30,7\ {\rm kJ} $

$ H_{\rm s} = \frac{-Q}{m} = \frac {30,70\ {\rm kJ}}{1,9\ {\rm g}} = 16,2\ {\rm kJ · g^{-1}} $

$ Δ_{\rm c}H_{\rm m} = – H_{\rm s} · M = -16,2\ {\rm kJ · g^{-1}} · 342\ {\rm g · mol^{-1}} = -5542\ {\rm kJ · mol^{-1}} $

c $ Δ_{\rm c}H_{\rm m} = 12 · Δ_{\rm f}H_{\rm m}^0 {\rm (CO_2)} + 11 · Δ_{\rm f}H_{\rm m}^0 {\rm (H_2O)} – Δ_{\rm f}H_{\rm m}^0 {\rm (C_{12}H_{22}O_{11})} $

$ Δ_{\rm f}H_{\rm m}^0 {\rm (C_{12}H_{22}O_{11})} = 12 · (-394\ {\rm kJ · mol^{-1}}) + 11 · (-286\ {\rm kJ · mol^{-1}}) -5542\ {\rm kJ · mol^{-1}} = -2332 {\rm kJ · mol^{-1}} $

Aufgabe 3:

Größe	Saccharose	Aspartam
physikalischer Brennwert H_s	16,2 kJ · g^-1	17 kJ · g^-1
physikalischer Brennwert H_bio	≈ H_s	≈ H_s
molare Verrennungsenthalpie $Δ_{\rm c} H_{\rm m}$	-5542 kJ · mol^-1	-4998 kJ · mol^-1
molare Bildungsenthalpie $Δ_{\rm f} H_{\rm m}$	-2332 kJ · mol^-1	-3092 kJ · mol^-1
molare Masse	343 g · mol^-1	294 g · mol^-1
Süßkraft	1	200

b Beide Stoffe haben einen ähnlichen Brennwert. Weil Aspartam aber 200-mal süßer schmeckt, muss nur ein Bruchteil zum Süßen verwendet werden. Der Nährwert von Aspartam kann also bei der Berechnung des Brennwerts eines Light-Produkts vernachlässigt werden. Unter Ernährungswissenschaftlern ist die Verwendung von Aspartam aber umstritten, da der süße Geschmack Hungergefühl auslösen kann. Dies kann u. U. sogar zu einer Gewichtszunahme führen. Außerdem handelt es sich um einen synthetischen Zuckerersatzstoff und nicht um einen natürlichen Nährstoff.

___________________________________________________________________________________

Seite 50

linke Spalte: Power-to-Gas-Technologie

Aufgabe 1:

$ {\rm H_2O(l)} \rightarrow {\rm H_2(g) + 0,5\ O_2(g)}$

Die Elektrolyse ist die Umkehrung der Bildung von
Wasser aus den Elementen, daher gilt:

$ Δ_{\rm r}H_{\rm m} {\rm (Elektrolyse)} = -Δ_{\rm f}H_{\rm m}{\rm (H_2O)} $

Aufgabe 2:

$ {\rm \color{purple}{a}} Δ_{\rm r}H_{\rm m} = Δ_{\rm f}H_{\rm m}^0 {\rm (CH_4)} + Δ_{\rm r}H_{\rm m}^0 {\rm (H_2O)} – Δ_{\rm r}H_{\rm m}^0 {\rm (CO)} $

$ -75 \ {\rm kJ · mol^{-1}} + (-242 \ {\rm kJ · mol^{-1}} ) -(-111 \ {\rm kJ · mol^{-1}} ) = -206 \ {\rm kJ · mol^{-1}} $

$ {\rm \color{purple}{b}}$ Es gilt der Satz von Hess:

1 H₂/ CO₂ ⇒ CH₄ / H₂O

2 H₂/ CO₂ ⇒ CO / H₂O

3 CO / H₂O ⇒ CH₄ / H₂O

$ (\color{orange}{3}) Δ_{\rm r}H_{\rm m} = (\color{blue}{2}) Δ_{\rm r}H_{\rm m} + (\color{green}{1}) Δ_{\rm r}H_{\rm m} $

$ = -41\ {\rm kJ · mol^{-1}} + (-165\ {\rm kJ · mol^{-1}}) = -206\ {\rm kJ · mol^{-1}} $

$ {\rm \color{purple}{c}}$ Die Werte sind identisch. Reaktion $ (\color{blue}{2}) $ und $ (\color{orange}{3}) $ sind Teilreaktionen (Zwischenschritte) von $ (\color{green}{1}) $, sodass der Satz von Hess gilt.

Aufgabe 3:

Es müssen erneuerbare Energiequellen (Wind, Solar, Wasser) genutzt werden, damit die Power-to-Gas- Technologie als umweltfreundlich gelten kann.

Seite 50

rechte Spalte: Brenngasbetriebene Autos

Aufgabe 1:

Chemische Energie des Erdgases wird in thermische Energie umgewandelt. Thermische Energie wird in mechanische Energie (Kolbenhub) umgewandelt. Mechanische Energie wird in mechanische Energie umgewandelt (Vortrieb des Autos). Bei jedem Umwandlungsschritt geht ein Teil der Energie „verloren“ und steht nicht für weitere Umwandlungen zur Verfügung.

Aufgabe 2:

a Brennwert: Verbrennungswärme, die beim Verbrennen von 1 kg bzw. m³ eines Brennstoffs freigesetzt wird unter Bildung von flüssigem Wasser
Heizwert: Verbrennungswärme, die beim Verbrennen von 1 kg bzw. m³ eines Brennstoffs freigesetzt wird unter Bildung von gasförmigem Wasser

$ Δ_{\rm c}H_{\rm m} = 0,4 · Δ_{\rm c}H_{\rm m} {\rm (Propan)} + 0,6 · Δ_{\rm c}H_{\rm m} {\rm (Butan)}$
$ = 0,4 · (−2220\ {\rm kJ · mol^{-1}} ) + 0,6 · (−2878\ {\rm kJ · mol^{-1}} ) = -2614,8\ {\rm kJ · mol^{-1}}$

$ H_{\rm s} = \frac{-Δ_{\rm c}H_{\rm m}}{M{\rm (Autogas)}} = \frac{2615\ {\rm kJ · mol^{-1}}}{52,4\ {\rm kJ · mol^{-1}}} = 49,9\ {\rm kJ · g^{-1}} = 49,9\ {\rm MJ · kg^{-1}}$

$ M {\rm (Autogas)} = 0,4 · M {\rm (Propan)} + 0,6 · M {\rm (Butan)}$
$ = 0,4 · (44\ {\rm g · mol^{-1}} ) + 0,6 · (58\ {\rm g · mol^{-1}} ) = 52,4\ {\rm g · mol^{-1}} $

Grundsätzlich gilt: $ H_{\rm s} > H_{\rm s}$. Im Brennwert ist die bei der Kondensation des Wassers freigesetzte Verdampfungsenthalpie enthalten. Die Verbrennungsprodukte im Motor sind gasförmig. Der Heizwert liefert daher eine genauere Aussage über die zur Nutzung verfügbare Energie.

Aufgabe 3:

a Weil alle an der Reaktion beteiligten Stoffe gasförmig vorliegen, gilt der Satz von Avogadro: Gleiche Gasvolumina enthalten gleich viele Teilchen, d. h., die stöchiometrischen Koeffizienten in der Reaktionsgleichung können als Volumen interpretiert werden.

C₄H₁₀(g) + 6,5 O₂(g) → 4 CO₂(g) + 5 H₂O(g)

⇒ 1 m³ + 6,5 m³ 4 m³ + 5 m³

⇒ 1 m³ + 6,5 m³ = 7,5 m³

⇒ 4 m³ + 5 m³ = 9 m³

ΔV = 9 m³ – 7,5 m³ = 1,5 m³
W = -p · ΔV = -101 325 N · m^-2 · 1,5 m³
= -151,99 kJ

b Der Heizwert von Butan beträgt 123 MJ ⋅ m^-3 , d. h., die Arbeit, die mit der Verbrennung verrichtet werden kann, ist im Vergleich zur Volumenarbeit aufgrund der Teilchenzahländerung sehr viel größer.

Aufgabe 4:

Es gibt viele Faktoren: Reifendruck, Straßenbeschaffenheit, Fahrzeuggewicht und -form, Getriebeübersetzung, Fahrweise, Zusatzverbraucher wie Klimaanlage, Licht und Radio.

________________________________________________________________

Seite 51

linke Spalte: Stickstoffoxide aus dem Diesel

Aufgabe 1:

a N₂(g) + O₂(g) → 2 NO(g)
2 NO(g) + O₂(g) → 2 NO₂(g)

b Synthese von Stickstoffmonooxid aus den Elementen:
Δ_RG⁰ = 2 · Δ_fG⁰(NO) = +173,2 kJ · mol^-1
Oxidation von Stickstoffmonooxid zu Stickstoffdioxid:
Δ_RG⁰ = 2 · Δ_fG⁰(NO₂) – 2 · Δ_fG⁰(NO) = -70,8 kJ · mol^-1
Nur für die letzte Reaktion ist Δ_RG⁰ < 0, d. h., nur sie ist
exergonisch und verläuft damit freiwillig.

c Die Bildung ist freiwillig, wenn Δ_RG negativ ist. Mithilfe der Gibbs-Helmholtz-Gleichung (Δ_RG = Δ_RH⁰ – T_G · Δ_RS⁰)
kann berechnet werden, ab welcher Temperatur Δ_RG negativ wird. Für die Grenztemperatur T_G gilt deshalb:

Δ_RG = 0

Δ_RH⁰ – T_G · Δ_RS⁰ = 0 ⇒ Umstellen nach T_G

T_G = Δ_RH⁰/Δ_RS⁰

Die molare Standardreaktionsentropie Δ_RS⁰ kann auch aus der Gibbs-Helmholtz-Gleichung mit T = 298 K (Standardbedingungen) berechnet werden:

Δ_RG = Δ_RH⁰ – T_G · Δ_RS⁰ ⇒ Umstellen nach Δ_RS⁰

$ {\rm Δ_RH^0 } = {\rm \frac {Δ_RH^0\ -\ Δ_RG^0}{T} } $

$ ≈ {\rm \frac {90 300\ J\ ·\ mol^{-1}\ -\ 86 600\ J\ ·\ mol^{-1}}{298\ K} } $

≈ 12,4 J · mol^-1 · K^-1

Für die Grenztemperatur T_G folgt damit:

$ {\rm T_G } ≈ {\rm \frac {90 300\ J\ ·\ mol^{-1}}{12,4\ J\ ·\ mol^{-1}\ ·\ K^{-1}} } $

≈ 7300 K

Hinweis: Der Berechnung liegt die Annahme zugrunde, dass Δ_RH und Δ_RS nicht von der Temperatur abhängen, d. h., dass Δ_RH = Δ_RH⁰ und Δ_RS = Δ_RS⁰

Aufgabe 2:

a Aus Aufgabe 1b folgt:

2 NO₂ → 2 NO + O₂
⇒ Δ_RG⁰(1) = + 70,8 kJ · mol^-1 (1)

2 NO → N₂ + O₂
⇒ Δ_RG⁰(2) = – 173,2 kJ · mol^-1 (2)

Beim Zerfall von Stickstoffdioxid in die Elemente Stickstoff und Sauerstoff laufen beide Reaktionen ab.
Δ_RG⁰ = Δ_RG⁰(1) + Δ_RG⁰(2) = -102,4 kJ · mol^-1.
Da Δ_RG⁰ < 0 ist die Reaktion exergonisch und damit freiwillig.

b Stickstoffdioxid ist metastabil gegenüber dem exergonischen Zerfall zu Stickstoff und Sauerstoff. Der Grund dafür liegt in der großen freien Aktivierungsenthalpie.

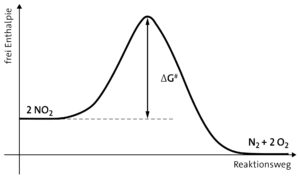
Aufgabe 3:

a 4 NH₃ + 6 NO → 5 N₂ + 6 H₂O

b Δ_RG⁰ = 6 · Δ_fG(H₂O(g)) – [4 · Δ_fG(NH₃(g)) + 6 · Δ_fG(NO(g))]

Δ_RG⁰ = -1371,6 kJ · mol^-1 – [-65,6 kJ · mol^-1 + 519,6 kJ · mol^-1]

Δ_RG⁰ = -1825,6 kJ · mol^-1

Mit Δ_RG⁰ < 0 verläuft die Reaktion exergonisch und damit freiwillig.

c Im Dieselmotor werden Kohlenwasserstoffe, der Diesel-Kraftstoff, mit heißer Luft in Kontakt gebracht, wodurch die Reaktion der Kohlenwasserstoffe mit dem Sauerstoff der Luft erfolgt (Verbrennung). Ist Sauerstoff im Überschuss vorhanden, kann er bei den hohen Temperaturen im Abgasstrom mit dem Stickstoff der Luft zu Stickstoffoxiden reagieren. Stickstoffoxide gelten als Schadstoffe, sodass eine Reinigung des Abgases notwendig wird.

rechte Spalte: Freiwillig muss es sein

Aufgabe 1:

a Bei der Synthese des Polymers aus den Monomeren sinkt die Zahl der unabhängig voneinander beweglichen Teilchen. Es wird erwartet, dass die Entropie abnimmt, d. h., dass die Reaktionsentropie negativ ist. Diese Erwartung stimmt mit den Werten in Tabelle 4, S. 51 überein.

b Die freie Reaktionsenthalpie ist in beiden Fällen negativ. Das heißt, die Reaktionen verlaufen exergonisch und damit freiwillig.

c Grundlage ist die Gibbs-Helmholtz-Gleichung:
Δ_rG = Δ_rH – T · Δ_rS
PE: Δ_rH = Δ_rG + T · Δ_rS ≈ -92 kJ · mol^-1
PP: Δ_rS = (Δ_rH – Δ_rG) : T ≈ -114 J · mol^-1 · K^-1
PS: Δ_rG = Δ_rH – T · Δ_rS ≈ -40 kJ · mol^-1

Aufgabe 2:

a Aus der Gibbs-Helmholtz-Gleichung
Δ_rG = Δ_rH – T · Δ_rS
folgt: Die freie Reaktionsenthalpie nimmt mit steigender Temperatur zu, weil die Reaktionsentropie bei allen drei Reaktionen negativ ist.

b Ausgehend von der Gibbs-Helmholtz-Gleichung gilt für die Ceiling-Temperatur T_C:
Δ_rG = Δ_rH – T_C · Δ_rS = 0
Daraus folgt:

T_C = Δ_rH/Δ_rS

PE: T_C ≈ 640 K
PP: T_C ≈ 740 K
PS: T_C ≈ 680 K

c Um die Polymere herzustellen, muss die Polymerisation freiwillig verlaufen, d. h., die Reaktionstemperatur muss unterhalb der Ceiling-Temperatur liegen.

d Alle drei Polymerisationsreaktionen sind exotherm. Die Reaktionswärme führt ohne Kühlung zu einem Anstieg der Temperatur im System. Um ein Erreichen oder Überschreiten der Ceiling-Temperatur zu vermeiden, muss das Reaktionsgefäß gekühlt werden.