Fotoeffekt
Aufgabe 1
a) Aufbau zur Gegenfeldmethode:
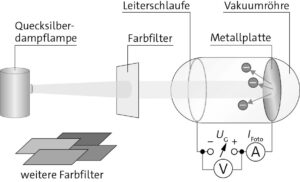
b) Aus der Quecksilberdampflampe gelangen Photonen. Mit Farbfiltern kann die Wellenlänge selektiert werden. Anschließend gelangen Photonen einer bestimmten Wellenlänge zwischen Kathode und Anode (Metallplatte). Ist ihre kinetische Energie groß genug, gelangen sie zur Metallplatte und lösen dort Elektronen aus, die dann als Fotostrom gemessen werden können.
Bei der Gegenfeldmethode wird die Gegenspannung so eingestellt, dass gerade kein Fotostrom mehr fließt. So kann man auf die kinetische Energie der Elektronen schließen, die durch die Strahlung austreten. Je größer die Frequenz der einfallenden Strahlung ist, umso höher ist die kinetische Energie der Elektronen. Die Intensität der Strahlung beeinflusst die Energie hingegen nicht. Dies ist der lichtelektrische Effekt oder Fotoeffekt. Der Versuch zeigt, dass Strahlung auch Teilcheneigenschaften besitzt.
Deutung: Modelliert man die Strahlung als Photonen mit einer bestimmten Energie \(E_{rm ph} = h \cdot f = h \cdot \frac{c}{\lambda}\) , kann man den Effekt erklären. Wenn ein Photon auf die Zinkplatte trifft, gibt es seine Energie ab. Ist diese groß genug, um Elektronen aus dem Material zu lösen, sind diese frei beweglich. Ist die Frequenz größer als eine Grenzfrequenz \(f_g\) , steigt die Elektronenenergie linear mit der Frequenz der Strahlung. Wenn man die Messwerte durch eine Gerade mit der Steigung \(h\) und Achsenabschnitt \(E_{\rm ab}\) beschreibt, kann man aus dem Steigungsdreieck im Diagramm das Plancksche Wirkungsquantum ermitteln.
Aufgabe 2
a) Ein Teil der abgelösten Elektronen trifft auf den Ring. Dadurch beginnt der Ring, sich aufzuladen. Aufgrund der dadurch entstehenden Spannung fließen Elektronen über die Spannungsquelle und das Amperemeter zur Kathode.
b) Je höher die Gegenspannung, umso größer muss die kinetische Energie eines Elektrons sein, um den Ring zu erreichen. Aufgrund der Geschwindigkeitsverteilung der Elektronen schaffen es deshalb mit wachsender Gegenspannung immer weniger Elektronen zum Ring, entsprechend nimmt die Stromstärke ab. Wenn die maximale Energie der abgelösten Elektronen zu klein ist, um das elektrische Feld zu überwinden, dann ist die Stromstärke null.
c) Je größer die Lichtintensität, umso mehr Elektronen werden abgelöst, umso mehr Elektronen erreichen den Ring und können abfließen, umso größer ist also der Fotostrom..
d) Die maximale Energie der abgelösten Elektronen bestimmt die Gegenspannung, bei der der Fotostrom zum Erliegen kommt. Diese Energie hängt allein von der Photonenenergie des verwendeten Lichts ab.
Aufgabe 3
a)
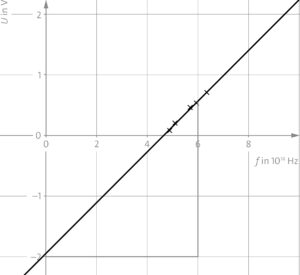
b) Die Steigung beträgt für \(\Delta U=2,5\,{\rm V}\) und \(\Delta f=6\cdot 10^{14}\,{\rm Hz}\):
\(\frac{\Delta E}{\Delta f}=\frac{e\cdot \Delta U}{\Delta f}=6,7\cdot 10^{-34}\,{\rm Js}\)
Aus dem Hochachsenabschnitt ergibt sich eine Ablöseenergie von knapp 2 eV.
c) Aus dem Querachsenabschnitt ergibt sich eine Grenzfrequenz von etwa \(4,8 \cdot 10^{14}\,{\rm Hz}\). Das entspricht einer Grenzwellenlänge von \(\lambda_g=\frac{c}{f_g}=625\,{\rm nm}\).
d) Der Graph muss die gleiche Steigung haben und die Hochachse für \(U = –1,0\,{\rm V}\) schneiden.
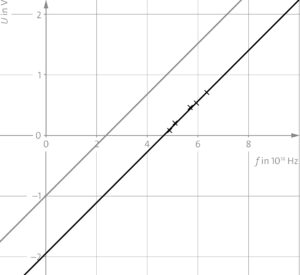
e) \(E_{\rm ab}=h\cdot f_g=h\cdot\frac{c}{\lambda_g}\) \(\Rightarrow \lambda_g=\frac{h\cdot c}{E_{\rm ab}}=1,2\cdot 10^{-6}\,{\rm m}\)
Aufgabe 4
a) Die Photonen des infraroten Lichts haben nicht genug Energie, um Elektronen aus dem Cäsium abzulösen. Bei violettem Licht sind die Photonen energiereicher, Elektronen werden abgelöst.
Berechnung der Grenzwellenlänge aus \(E_{\rm ab}=2,1\,{\rm eV}\):
\(\lambda_g=\frac{h\cdot c}{E_{\rm ab}}=592\,{\rm nm}\)
Infrarotes Licht hat eine größere Wellenlänge als 592 nm, violettes Licht eine kleinere.
b) \(e\cdot U=E_{\rm ph}-E_{\rm ab}=\frac{h\cdot c}{\lambda}-E_{\rm ab}\)
\(\Rightarrow U=\frac{1}{e}\cdot\left(\frac{h\cdot c}{\lambda}-E_{\rm ab}\right)=0,86\,{\rm V}\)
c) \(Q=C\cdot U=2,0\cdot 10^{-9}\,{\rm F}\cdot 0,89\,{\rm V}=1,7\cdot 10^{-9}\,{\rm C}\)
d) Kathode und Anode der Fotozelle bilden einen Kondensator mit sehr kleiner Kapazität, der sich aufgrund des Fotoeffekts auflädt. Durch Parallelschließen des Kondensators fließt ein Großteil der Ladung von der Fotozelle auf den Kondensator. An Kondensator und Fotozelle liegt also parallel die gleiche allmählich anwachsende Gegenspannung an. Dadurch nimmt die Stromstärke immer mehr ab, bis auch die schnellsten abgelösten Elektronen die Anode nicht mehr erreichen.
e) Da die kinetische Energie der Elektronen von der Wellenlänge der eintreffenden Strahlung abhängt, verändert sich die Beobachtung mit der Änderung der Wellenlänge. Eine größere Frequenz (kleinere Wellenlänge) führt zu einer größeren kinetischen Energie und damit zu einem größeren Fotostrom.
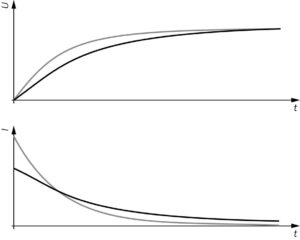
f) Bei größerer Intensität ist die Stromstärke anfangs größer, dadurch lädt sich der Kondensator schneller auf, seine Spannung ist für große Zeiten aber genauso hoch wie bei kleinerer Intensität. Die roten Graphen stehen für die höhere Intensität. Die Flächen für die Graphen im \(I(t)\)-Diagramm muss gleich sein.
Interferenz von Materie
Aufgabe 1
a) Energieerhaltung: \(\frac{1}{2}\cdot m\cdot v^2=e\cdot U_B\)
Impuls: \(p=m\cdot v=m\cdot \sqrt{\frac{2\cdot e\cdot U_B}{m_e}}=\sqrt{2\cdot m\cdot e\cdot U_B}=2,4\cdot 10^{-23}\,{\rm kg}\cdot \frac{\rm m}{\rm s}\)
b) \(\lambda=\frac{h}{p}=2,7\cdot 10^{-11}\,{\rm m}\)
c) Da \(𝑑 ≪ 𝑎\) und \(𝜆 ≪ 𝑑\) (wegen der 2. Bedingung gibt es zahlreiche Maxima), verwenden wir die Kleinwinkel-Näherung \(\frac{\lambda}{d}=\frac{x_1}{a}\):
\(x_1=a\cdot\frac{\lambda}{d}=0,25\,{\rm m}\cdot\frac{\rm 2,7\cdot 10^{-11}\,m}{\rm 2,0\cdot 10^{-6}\,m}=3,4\,{\rm µm}\)
Aufgabe 2
a) Im klassischen Wellenmodell würden sich auf jedem Schirmort die Elementarwellen der beiden Spalte überlagern. Man würde also nicht nur einige wenige Nachweisorte erhalten, sondern für jedes Elektron eine weit über den Schirm verteilte Nachweisfläche.
b) Klassische Teilchen gehen entweder durch den einen Spalt oder durch den anderen Spalt. Sie zeigen keine Interferenz. Bei klassischen Teilchen könnte man nur zwei Streifen beobachten; einen für den linken und einen für den rechten Spalt.
Doppelspaltexperiment
Aufgabe 1
a) Die Wellenlänge beträgt \(\lambda=\frac{h}{p}=6,7\cdot 10^{-37}\,{\rm m}\).
b) Für die Beugung am Doppelspalt mit Spaltabstand \(g\) gilt in erster Ordnung für den Beugungswinkel \(\beta\): \(\sin(\beta) = \frac{λ}{g}\). Wir lösen nach \(g\) auf: \(g = \frac{λ}{\sin(\beta)} = 3,8 \cdot 10^{–32}\,{\rm m}\).
Da der Läufer nicht durch einen so engen Spalt passt, kann er die Beugung nicht selbst ausprobieren.
c) Für die Beugung am Doppelspalt mit Spaltabstand \(g = 0,5\,{\rm m}\) gilt in erster Ordnung für den Beugungswinkel \(\beta\) dann: \(\sin(\beta)=\frac{\lambda}{g}\)
Wir lösen nach \(\beta\) auf: \(\beta=\arcsin\left(\frac{\lambda}{g}\right)=7,7\cdot 10^{-35}°\)
Aufgabe 2
a) Bereits im dritten Bild (4 h 15′) gibt es eine orangefarbene Stelle in der Mitte. Gemäß dem Farbcode könnte es sich bereits hier um eine Stelle handeln, bei der 10 oder mehr counts/pixel festgestellt wurden. Beim vierten Bild wurden in der Bildmitte auf jeden Fall deutlich mehr als 10 counts/pixel gezählt.
b) Im ersten Bild wird deutlich, dass die Heliumatome stets als Ganzes nachgewiesen werden und dass die Nachweisorte zufällig verteilt sind. Bereits beim zweiten Bild kann man erkennen, dass sich ein Interferenzmuster bildet.
c) In den ersten 5 min werden etwa 100 Quantenobjekte nachgewiesen. Im Mittel wird also etwa alle 3 s ein Heliumatom in die Apparatur geschickt. Die Durchflugzeit eines Heliumatoms beträgt weniger als 0,001 s. Man kann also damit rechnen, dass sich praktisch immer nur ein Heliumatom in der Anordnung befindet.
Aufgabe 3
a) De-Broglie-Wellenlänge für den Fußball:
\(\lambda=\frac{h}{m\cdot v}=\frac{\rm 6,63\cdot 10^{-34}\,Js}{\rm 0,430\,kg\cdot 10\,\frac{\rm m}{\rm s}}=1,5\cdot 10^{-34}{\rm m}\)
De-Broglie-Wellenlänge für das Virus:
\(\lambda=\frac{h}{m\cdot v}=\frac{\rm 6,63\cdot 10^{-34}\,Js}{\rm 1\cdot 10^{-20}\,kg\cdot \,\frac{\rm m}{\rm s}}=7\cdot 10^{-15}{\rm m}\)
De-Broglie-Wellenlänge für das Fullerenmolekül: Die Masse ist durch die 60 Kohlenstoff-Atome mit je einer Masse von \(m_C=12\text{u}\) gegeben:
\(m=60\cdot m_C=60\cdot 12\text{u}=60\cdot 12\cdot 1,66\cdot 10^{-27}\,{\rm kg}=1,20\cdot 10^{-24}\,{\rm kg}\)
\(\lambda=\frac{h}{m\cdot v}=\frac{\rm 6,63\cdot 10^{-34}\,Js}{\rm 1\cdot 10^{-20}\,kg\cdot \,\frac{\rm m}{\rm s}}=7\cdot 10^{-15}{\rm m}\)
b) Kleinwinkel-Näherung: \(\frac{\lambda}{g}=\frac{x_1}{a}\)
Virus: \(x_1=a\cdot\frac{\lambda}{g}=1,00\,{\rm m}\cdot\frac{\rm 7\cdot 10^{-15}\,m}{\rm 150\cdot 10^{-9}\,m}=4,7\cdot 10^{-8}\,{\rm m}\)
Fulleren: \(x_1=a\cdot\frac{\lambda}{g}=1,00\,{\rm m}\cdot\frac{\rm 5,5\cdot 10^{-11}\,m}{\rm 150\cdot 10^{-9}\,m}=3,7\cdot 10^{-4}\,{\rm m}\)
c) Fußball: \(x_1=a\cdot\frac{\lambda}{g}=1,00\,{\rm m}\cdot\frac{\rm 1,5\cdot 10^{-34}\,m}{\rm 0,5\,m}=3\cdot 10^{-34}\,{\rm m}\)
d) Bei Fullerenen und womöglich in nicht zu ferner Zukunft auch bei Viren kann das Interferenzmuster mit Hightech-Detektoren aufgelöst werden. Das Interferenzmuster von Fußbällen ist jedoch, auch wegen des notwendigerweise großen Spaltmittenabstands, noch einmal um etwa 30 Größenordnungen feiner und somit nicht beobachtbar.
Hinweis: Dazu kommt noch die Tatsache, dass Fußbälle stark mit ihrer Umgebung wechselwirken und auch deshalb kein Interferenzmuster beobachtet werden kann (Welcher-Weg-Information).
Determiniertheit
Aufgabe 1
Determiniertheit: Gesetzmäßigkeiten erlauben es, Phänomene zu beschreiben und vorherzusagen. Das nennt man Determiniertheit. Theoretische Modelle bilden dabei möglichst genau ab, was in der Natur passiert.
Zufall: Gleichzeitig sind einzelne Prozesse wie z. B. der genaue Zeitpunkt für den Zerfall eines Atomkerns nicht vorhersagbar und geschehen „zufällig“. Hier kann die Physik Gesetzmäßigkeiten aufstellen und statistisch vorhersagen, wie sich ein Prozess entwickelt. Der Zerfall einzelner Kerne lässt sich aber nach der Quantenphysik nicht genau beschreiben.
Stochastische Abhängigkeit bedeutet, dass die Eigenschaften von Quantenobjekten nicht voneinander unabhängig sind. Dies kann auch Messungen in Experimenten beeinflussen: Wenn Quantenobjekte miteinander wechselwirken, werden sie verschränkt. Das bedeutet, wenn in einem Prozess z. B. zwei Photonen entstehen, sind ihre Impulse und Polarisationen stochastisch abhängig. Misst man z. B. die Polarisation des einen Photons in einer Messung, so ist sofort auch die Polarisation des anderen Objekts davon betroffen und sie korrelieren. Verschränkte Objekte sind also in ihren Eigenschaften stochastisch voneinander abhängig.
Aufgabe 2
Wären z. B. die Ergebnisse eines Interferenzexperiments beliebig, dann wäre nach vielen Wiederholungen nicht zuverlässig ein Muster erkennbar, bei dem man sogar die Abstände der Maxima vorhersagen kann. Einzelne Nachweisorte sind zwar nicht vorhersagbar, man kann aber z. B. sagen, dass im Bereich eines Minimums deutlich weniger Quantenobjekte nachgewiesen werden als im Bereich eines Maximums. Dabei ist durch die Wellenlänge der Quantenobjekte und die Geometrie der Anordnung festgelegt, wo die Maxima und Minima auftreten.
Aufgabe 3
a)
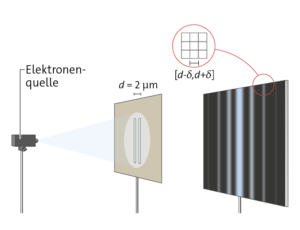
b) Entsprechend ihrer Wellenlänge werden die Elektronen am Doppelspalt gebeugt und es entsteht ein Interferenzmuster auf dem Schirm. Die Elektronen treffen auf einen Pixel des Snensor im Intervall \([d-\delta,d+\delta]\). Alle Elektronen in diesem Bereich werden von dem Sensor gezählt und der Stelle \(d\) zugeordnet. Das bedeutet, dass die Counts zu Signalen mit Abstand \(d\) führen. Das heißt auch, dass die Auflösung des Detektors nicht besser als \(\delta\) ist.
c) Für die Geschwindigkeit gilt: \(v=\sqrt{\frac{2\cdot e\cdot \cdot U_B}{m_e}}=132\,600\,\frac{\rm km}{\rm s}\)
Für den Impuls gilt: \(p=m\cdot v=1,208\cdot 10^{-22}\cdot {\rm kg}\cdot\frac{\rm m}{\rm s}\)
d) Für konstruktive Interferenz gilt: \(\lambda=\frac{g\cdot d}{a}=5,5\cdot 10^{-11}=5,5\,{\rm pm}\)
e) Wir berechnen die De-Broglie Wellenlänge mit dem Impuls aus Teilaufgabe c): \(\lambda=\frac{h}{p}=5,485\,{\rm pm}\)
Damit sind die berechnete und die im Experiment gefundene Wellenlänge gleich.
f) Es gilt: \(2\cdot d\sin(\vartheta)=\lambda\)
Der Glanzwinkel beträgt demnach \(\vartheta=\arcsin\left(\frac{\lambda}{2\cdot d}=1,281°\right)\).
Quantenmechanisches Atommodell
Aufgabe 1
a) Solange keine Ortsmessung durchgeführt wird, kann man dem Elektron tatsächlich keinen Ort zuschreiben. Sobald eine Ortsmessung gemacht wird, ist der Ort bestimmt (so gut wie die Ortsauflösung des Detektors ist).
b) Dies stimmt zwar beim Grundzustand, aber schon beim ersten angeregten Zustand gibt es einen kugelförmigen Bereich zwischen der zentralen Wolke und der Wolke darum herum, auf dem die Nachweiswahrscheinlichkeit praktisch 0 ist.
c) Das ist falsch, s. Teilaufgabe a). Nach der Ortsmessung ist die Wolke kollabiert.
d) Richtig. Die Nachweiswahrscheinlichkeit, das Elektron irgendwo nachzuweisen, ist immer gleich 1.
Aufgabe 2
a) Beim Teilchenmodell wird das Atom bzw. das Molekül als kleines, hartes Kügelchen beschrieben. Das Kern-Hülle-Modell ist detaillierter: Um einen kleinen positiv geladenen Kern befindet sich eine ausgedehnte negativ geladene Elektronenhülle.
b)
- Verschiebungspolarisation, wie sie z. B. in einem Dielektrikum vorkommen kann.
- Das Experiment von Rutherford. Schnelle Alpha-Teilchen durchdringen Atome zum großen Teil ohne stark abgelenkt zu werden.
c) Das Teilchenmodell ist einfacher. Für eine Beschreibung der Aggregatszustände oder der Wärmebewegung in Körpern ist das Kern-Hülle-Modell nicht nötig.
Einzelphotonen
Aufgabe 1
\(E=200\,{\rm keV}=200*1000*1,6\cdot 10^{-19}\,\,{\rm J}=3,2\cdot 10^{-14}\,{\rm J}\)
\(E_{\rm ph}=\frac{h\cdot c}{\lambda}\Rightarrow \lambda=\frac{h\cdot c}{E_{\rm ph}}=6,2\,{\rm pm}\)
\(p=\frac{h}{\lambda}=1,1\cdot 10^{-22}\,{\rm kg}\cdot\frac{\rm m}{\rm s}\)
Aufgabe 2
Die Energie des Gamma-Photons ist \(E=1,55\,{\rm eV}=2,48\cdot 10^{-19}\,{\rm J}\) und damit \(1,29 \cdot 10^5-mal so groß wie vom Photon des roten Lichts. Damit ist die Wellenlänge des Photons des roten Lichts etwa 129 000-mal so groß und der Impuls um den Faktor 129 000 kleiner als beim Gamma-Photon.
Aufgabe 3
a) Der Doppelspalt wird so aufgebaut, dass der Spaltmittenabstand \(g\) dreimal größer ist als die Spaltbreite \(b\). Dadurch unterscheidet sich das Beugungsmuster des Doppelspalts deutlich von dem des Einzelspalts. Beim Doppelspaltexperiment werden einzelne Photonen durch den Doppelspalt geschickt. Das Interferenzmuster auf dem Schirm ist um so deutlicher zu sehen, wenn mehr Photonen nacheinander durch den Doppelspalt geschickt
werden. Ein einzelnes Photon, das auf einen Doppelspalt trifft, wird am gesamten Doppelspalt gebeugt, sodass viele Photonen langfristig das Beugungsmuster des Doppelspalts erzeugen.
Wenn ein einzelnes Photon auf einen Doppelspalt trifft, dann wird es am gesamten Doppelspalt gebeugt, sofern keine Welcher-Weg-Information vorliegt.
Wenn dagegen Welcher-Weg-Information vorliegt (z. B. durch den Einsatz von Polarisationsfiltern), dann kann das Photon nur einen Spalt passiert haben und es entsteht das Beugungsmuster des Einzelspalts.
b) Zunächst betrachten wir den Aufbau des Interferometers mit Laserlicht. Abgebildet ist das Mach-Zehnder-Interferometer auch im Prüfungstraining auf Seite 91.
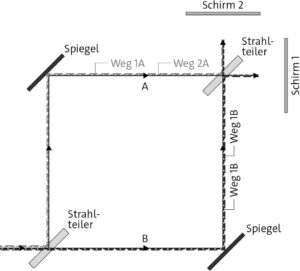
Die Lichtwellen fallen auf einen Strahlteiler und werden in zwei Teilwellen aufgespalten. Mithilfe zweier Spiegel werden die beiden Teilwellen dann auf einen zweiten Strahlteiler gelenkt. Wir setzen voraus, dass die vier Wege gleich lang sind. Die Wellen, die auf die Schirme fallen, bestehen jeweils aus zwei zusammengeführten Teilwellen. Am Schirm kommt es dann zur Interferenz, wobei sich die Interferenzmuster bei den beiden Schirmen unterscheiden.
Auch wenn nur ein Photon den Aufbau durchquert und Detektoren eingesetzt werden, die einzelne Photonen nachweisen können, wird Detektor 2 nicht ansprechen. Wenn man einzelne Photonen nacheinander durch den Aufbau schickt, entsteht das bekannte Interferenzmuster. Das Interferenzmuster auf dem Schirm ist um so deutlicher zu sehen, je mehr Photonen nacheinander durch den Aufbau geschickt werden.
Für Quantenobjekte gilt die Komplementarität: Interferenz und Weginformation schließen sich gegenseitig aus. Die Interferenz entsteht durch die Überlagerung der Wellenfunktionen, die die Ausbreitung des Photons beschreiben. Dem Photon ist kein eindeutiger Weg zuschreibbar. Dies ist ein reiner Quanteneffekt. Wenn dem Photon z. B. durch den Einsatz von Polarisationsfiltern ein Weg zuschreibbar ist, dann tritt kein Interferenzmuster mehr auf.
c) Bei beiden Experimenten entstehen Interferenzmuster, wenn keine Welcher-Weg-Information vorliegt. Bei beiden Experimenten gilt die Komplementarität: Interferenz und Welcher-Weg-Information schließen sich gegenseitig aus. Die Interferenz entsteht durch die Überlagerung der Wellenfunktionen, die die Ausbreitung des Photons beschreiben. Dem Photon ist kein eindeutiger Weg zuschreibbar. Dies ist ein reiner Quanteneffekt.
Wenn dem Photon z. B. durch den Einsatz von Polarisationsfiltern ein Weg zuschreibbar ist, dann tritt kein Interferenzmuster mehr auf.
Beim Mach-Zehnder-Interferometer kommen zwei Schirme zum Einsatz. Es gibt insgesamt vier Wege im Interferometer. Zu jedem Schirm führen zwei Wege. Beim Doppelspaltexperiment gibt es zwei Wege zum Schirm.
d) Wie schon in c) erkannt, gilt bei beiden Experimenten die Komplementarität: Interferenz und Weginformation schließen sich gegenseitig aus. Die Interferenz entsteht durch die Überlagerung der Wellenfunktionen, die die Ausbreitung des Photons beschreiben. Dem Photon ist kein eindeutiger Weg zuschreibbar. Dies ist ein reiner Quanteneffekt. Wenn dem Photon z. B. durch den Einsatz von Polarisationsfiltern ein Weg zuschreibbar ist, dann tritt kein Interferenzmuster mehr auf.
Aufgabe 4
a) Beschreibung des Mach-Zehnder-Interferometers: Siehe Lösung zu Aufgabe 3b).

Beim Michelson-Interferometer wird ein Lichtbündel an einem halbdurchlässigen Spiegel aufgeteilt und anschließend wieder zusammengeführt, sodass die Teilbündel interferieren. Sind die Weglängen \(𝑙_1\) und \(𝑙_2\) der beiden Arme des Interferometers gleich lang, ergibt sich im Zentrum des kreisförmigen Interferenzmusters ein Maximum.
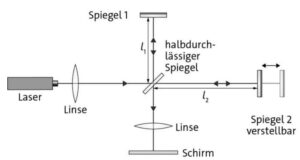
Ändert man die Weglänge eines Arms durch Verstellen des äußeren Spiegels um \(\Delta 𝑙\), dann ergibt sich ein Gangunterschied \(𝑑\) zwischen beiden Strahlen, der zur Änderung des Interferenzmusters führt. Dabei gilt \(𝑑 = 2 \cdot \Delta 𝑙\). Wird die Position des Spiegels langsam verändert, dann scheinen die Interferenzringe langsam nach außen zu wandern. Aus der Anzahl \(𝑘\) der durchlaufenden Maxima lässt sich bei bekannter Wellenlänge des Lasers die Änderung der Armlänge berechnen:
\(𝑑 = 2\cdot\Delta 𝑙 = 𝑘\cdot 𝜆 \leftrightarrow \Delta 𝑙 = 𝑘\cdot \frac{𝜆}{2}\) mit \(𝑘 = 1,\ 2,\ 3\dots\)
b) Bei beiden Interferometern ist ein Interferenzbild auf dem Schirm zu sehen. Beim Michelson-Interferometer gibt es allerdings nur einen Schirm, bei dem das Interferenzbild beobachtet werden kann. Beim Mach-Zehnder-Interferometer sind Interferenzbilder auf zwei Schirmen zu sehen. Die Interferenzbilder sind zueinander komplementär, wenn alle Weglängen im Interferometer gleich lang sind.
c) Hier sind die zwei Wege zum Detektor X eingezeichnet. Analog sind die zwei Wege zum Detektor Y einzuzeichnen:
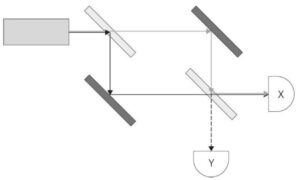
d) Der Gangunterschied der beiden Wege zu Detektor X ist idealerweise 0, der beiden Wege zu Detektor Y beträgt (aufgrund der Reflexionen) \(0,5\cdot λ\). Es tritt also destruktive Interferenz auf.
e) Wenn der Zünder da ist, dann kann er ausgelöst werden. Dies ist eine Ortsmessung, der Knaller explodiert, weder X noch Y geben ein Signal. Die Wahrscheinlichkeit dafür beträgt 50 %, weil die Strahlteiler 50 %-Strahlteiler sind. Wenn der Zünder nicht ausgelöst wird, dann kann Detektor X oder Detektor Y ein Signal geben. Beides ist gleich wahrscheinlich, weil der zweite Strahlteiler auch ein 50 %-Strahlteiler ist: P(X) = P(Y) = 25 %. Es gibt keine
Überlagerung, weil der Weg über den Knaller nicht möglich ist.
f) Ohne Zünder gibt Detektor Y (idealerweise) nie ein Signal. Wenn Detektor Y also nun ein Signal gibt, weiß man, dass der Knaller einen Zünder enthält, obwohl das Photon dort nicht absorbiert wurde. Irgendwie tastet das Photon also die gesamte Apparatur ab, dies wird mathematisch so dargestellt, dass die P-Wolke sich auf allen Wegen ausbreitet, bis es beim Nachweis zum Kollaps der Wolke kommt. Der wechselwirkungsfreie Nachweis des Knallers
klappt also nicht immer, aber immerhin in 25 % der Fälle.
Heisenbergsche Unbestimmtheitsrelation
Aufgabe 1
\(\Delta x\cdot \Delta p=10^{-10}\,{\rm m}\cdot 0,2\cdot 3\cdot 10^{-24}\,\frac{\rm kg\cdot m}{\rm s}=6\cdot 10^{-35}\,{\rm J}>\frac{h}{4\pi}=5,28\cdot 10^{-35}\,{\rm J}\)
Aufgabe 2
\(\Delta m\cdot m\cdot \Delta v\ge \frac{h}{4\pi}\)
\(\Rightarrow \Delta v\ge \frac{h}{4\pi\cdot\Delta x\cdot m}=3\cdot 10^{-29}\,\frac{\rm m}{\rm s}\)
Aufgabe 3
Der Impuls beträgt \(p = \frac{h}{λ} = 1,66 \cdot 10^{–27}\,{\rm kg} \cdot\frac{\rm m}{\rm s}\).
Der mittlere Querimpuls ist null. Aber die Standardabweichung des Querimpulses \(\Delta p\) hat gemäß der Unbestimmtheitsrelation den folgenden minimalen Betrag:
\(\Delta p \ge \frac{h}{(4π \cdot Δx}\). Dabei ist \(Δx\) die Standardabweichung des Ortes. Diese entspricht ungefähr dem Radius \(R\) der Pupille, \(R \approx Δx\). Mit dieser Näherung erhalten wir: \(Δp \ge \frac{h}{4π \cdot R} = 1,17 \cdot 10^{–32}\,{\rm kg}\cdot\frac{\rm m}{\rm s}\).
Aufgabe 4
a) Photonen sind Quantenobjekte und bei Radiowellen sind die Periodendauern so lang, dass man sie experimentell gut messen kann.
b) Bei Radiowellen kann man experimentell Frequenzen und Spektren prinzipiell ermitteln.
c) Photonen sind Quantenobjekte. Daher erfüllen sie die Unbestimmtheitsrelation \(Δt \cdot Δf \ge \frac{1}{4π}\) oder \(\delta f \cdot \delta t \ge \frac{1}{π}\). Dabei ist \(Δf\) die Standardabweichung der Frequenzmessung und kann experimentell erst bei vielen Photonen deutlich ermittelt werden.
d) Photonen sind Quantenobjekte. Daher haben sie auch Welleneigenschaften. Diese Welleneigenschaften verhalten sich bei zwei Photonen wie bei dem Zwei-Ton-Klang.
e) Ein Photon hat die Energie \(E = h \cdot f\). Entsprechend erweitern wir die Unbestimmtheitsrelation \(Δt\cdot Δf \ge \frac{1}{(4π}\) mit \(h\) und erhalten \(Δt \cdot ΔE \ge \frac{h}{(4π}\).
Verschränkung und Komplementarität
Aufgabe 1
a) Quantenhafter Nachweis: Es werden Ereignisse gezählt, jeder Nachweis eines Atoms an einem bestimmten Punkt des Schirms ist ein Ereignis.
Stochastisches Verhalten: Man kann nicht vorhersagen, wo auf dem Schirm ein Atom nachgewiesen wird, man kann für verschiedene Schirmorte nur Wahrscheinlichkeiten für den Nachweis angeben. Interferenzfähigkeit: Wenn man viele Nachweisorte sammelt, erhält man ein Interferenzmuster.
b) Wenn die Wege unterscheidbar sind, hat man eine Welcher-
Weg-Information. Dies ist bei der Hälfte der Atome der Fall. Dies führt dazu, dass diese Atome nicht zu einem Interferenzmuster beitragen. Die anderen Atome tragen dagegen weiterhin zu dem Muster bei. Dementsprechend ist das blaue Interferenzmuster deutlich weniger stark ausgeprägt ist als das rote.
Aufgabe 2
a) Dies folgt aus der Ladungserhaltung. Das Higgs-Teilchen ist elektrisch neutral, also muss die Summe der Ladungen der Zerfallsprodukte 0 sein.
b) Man kann das daraus schließen, dass die Messwerte für die Spins immer entgegengesetzt sind.
Aufgabe 3
a) Wie die Ladung ist auch der Impuls eine Erhaltungsgröße. Wenn das Higgs-Teilchen vor dem Zerfall Impuls 0 hat, dann muss auch die Summe der Impulse der entstehenden Teilchen 0 sein. Bei zwei entstehenden Teilchen müssen die Impulsvektoren entgegengesetzt (antilinear) sein, also bewegen sich die Teilchen in entgegengesetzte Richtungen.
b) Die Summe der Impulsvektoren der Zerfallsprodukte muss gleich dem Impulsvektor des Higgs -Teilchens vor dem Zerfall sein. Über die Bewegung eines einzelnen Zerfallsprodukts kann man nichts aussagen. Aber wenn sich das Higgs-Teilchen vor dem Zerfall in eine bestimmte Richtung bewegt hat, dann bewegt sich auch der Schwerpunkt der Zerfallsprodukte in diese Richtung.
c) Elektrisch geladene Elementarteilchen reagieren leichter mit Materie, weil diese auch aus elektrisch geladenen Teilchen besteht. So wird ein Neutron von Materie nur wesentlich abgelenkt, wenn es auf einen Atomkern trifft, während ein Proton die Abstoßung des Kerns auch erfährt, wenn es nicht direkt mit diesem zusammenstößt.
d) aus, weil in den Detektoren Protonen symmetrisch mit etwa gleichem Impuls aufeinandertreffen. Es gibt aber dennoch Asymmetrien, wenn z. B. in eine Richtung ein anderes Teilchen als in eine andere Richtung entsteht. So kann z. B. in einer Richtung ein Higgs-Teilchen entstehen, in der anderen z. B. ein Z-Boson. Diese Teilchen zerfallen auf unterschiedliche Weise, es gibt unterschiedliche Teilchenspuren.
© Cornelsen Verlag GmbH, Berlin