Postulate der Relativitätstheorie
Aufgabe 1
Bezugssystem: Niemand kann seine absolute Geschwindigkeit messen. Daher verwendet man bewegte Koordinatensysteme. Sie heißen Bezugssysteme
Inetrtialsystem: In der speziellen Relativitätstheorie betrachtet man unbeschleunigte Bezugssysteme, sie heißen Inertialsysteme.
Eigen- und Außensystem: Wenn sich ein Gegenstand relativ zu einem außenstehenden Beobachter bewegt, dann nennt man das Bezugssystem des Gegenstands Eigensystem und das des Beobachters Außensystem.
Aufgabe 2
Gleichzeitigkeit bezeichnet das Auftreten bzw. Beobachten eines Ereignisses zu einem bestimmten Zeitpunkt. Da die Zeit nach der speziellen Relativitätstheorie relativ ist, also vom betrachtenden Bezugssystem abhängt, ist auch das Auftreten eines Ereignisses abhängig vom Bezugssystem. In einem Bezugssystem können zwei Ereignisse gleichzeitig auftreten, während sie in einem anderen, relativ dazu bewegten, nicht gleichzeitig sind. Es gibt somit keine absolute Gleichzeitigkeit.
Aufgabe 3
1) In jedem Inertialsystem breitet sich Licht im Vakuum mit der gleichen Lichtgeschwindigkeit aus: c = 299 792 458 m/s
2) Die physikalischen Gesetze haben in allen Inertialsystemen dieselbe Form.
3) Weitere weniger grundlegende Naturgesetze kann man mit Transformationsregeln ineinander überführen.
Aufgabe 4
Konstanz der Lichtgeschwindigkeit (Postulat 1): Mit dem Michelson-Morley-Experiment kann nachgewiesen werden, dass Licht kein Medium braucht, um sich fortzubewegen. Mit diesem Experiment konnte die Äther-Theorie widerlegt und die Konstanz der Lichtgeschwindigkeit validiert werden.
Naturgesetze (Postulate 2 und 3): Die Aussendung je eines Lichtblitzes von zwei Raumstationen kann in verschiedenen Bezugssystemen zu unterschiedlichen Zeiten geschehen. In einem können sie gleichzeitig und in einem anderen zeitlich versetzt auftreten. Dennoch ist die Physik des Lichtes (Ausbreitung mit konstanter Geschwindigkeit ohne Medium) in allen Bezugssystemen gleich.
Minkowski-Diagramme
Aufgabe 1
a) Die Weltlinie des Radarsignals (rot) verläuft vier Kästchen nach rechts und vier Kästchen nach oben (von \(c \cdot \text{s}\) bis \(5 c \cdot \text{s}\)). Die Steigung beträgt also 1. Radarwellen breiten sich also mit Lichtgeschwindigkeit aus. Die Weltlinie des Autos (blau) verläuft vier Kästchen nach rechts und fünf Kästchen nach oben (von 0 bis \(5 c \cdot \text{s}\)). Die Steigung beträgt also 1,25. Das Auto fährt also mit der Geschwindigkeit \(0,8\,c\).
Das Radarsignal wird zum Zeitpunkt \(t_{\rm em} = 1\,{\rm s}\) emittiert und zum Zeitpunkt \(t_{\rm refl} = 5\,{\rm s}\) reflektiert. Da Hin- und Rückweg gleich lang sind, benötigt das Radarsignal für beide Wege die gleiche Zeit 4 s. Also wird es zum Zeitpunkt \(t_{\rm abs} = 9\,{\rm s}\) von der Radarpistole absorbiert. Da Hin- und Rückweg gleich lang sind, benötigt das Auto für beide Wege die gleiche Zeit 5 s. Also kommt es zum Zeitpunkt \(t_{\rm An} = 10\,{\rm s}\) wieder bei \(x = 0\) an.
b) Die Einheiten der beiden Achsen sind Lichtsekunden. Daher hat der Quotient von \(x\)- und \(y\)-Abschnitt keine Einheit, sodass der Tangens berechnet werden kann. Licht legt in einer Sekunde eine Lichtsekunde zurück, sodass der Tangens den Betrag 1 hat. Somit beträgt der Winkel 45°.
c) Die Geschwindigkeit ist der Quotient aus Weg und Zeit, \(v = \frac{Δs}{Δt}\). Das ist der Quotient aus dem horizontalen Abschnitt und dem vertikalen Abschnitt im Minkowski-Diagramm. Somit ist es der Tangens des Winkels \(\alpha\), den die Weltlinie mit der Zeitachse einschließt. Also ist die Geschwindigkeit gleich dem inversen Tangens von \(\alpha\), also \(v =\arctan \left(\frac{x}{t}\right)\).
Beispiel für das Auto: \(\frac{\Delta x}{\Delta t}=v=0,8\cdot c\)
\(\Rightarrow\arctan(\alpha)=\arctan \left(\frac{x}{t}\right)=\arctan \left(\frac{4\,c\cdot\text{s}}{5\,c\cdot\text{s}}\right)=38,65°\)
Das sieht man auch in der Abbildung.
Aufgabe 2
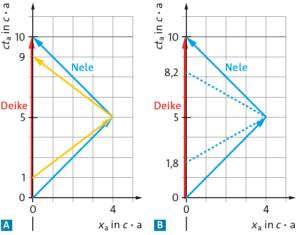
a) Nele legt nur 6 Jahre Eigenzeit \(Δt\) zurück, während auf der Erde \(Δt_a = 10 \) Jahre vergehen:
\(\frac{10}{6}=\frac{\Delta t_a}{\Delta t}=\gamma=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\)
Auflösen nach \(v\) bringt: \(v=0,8\cdot c\)
b) Bis zum Umkehren vergeht die Hälfte der Zeit, also \(\Delta t_{a,1/2}=5\,\text{a}\) auf der Erde. Damit folgt: \(s=v\cdot\Delta t_{a,1/2}=0,8\,c\cdot 5\,\text{a}=5\,c\cdot\text{a}\)
c) Deikes Weltlinie ist rot, Neles Weltlinie Blau und die des Lichtes gelb dargestellt. Die Punkte auf der gestrichelten Linie sind in Neles Bezugssystem gleichzeitig.
Aufgabe 3
a) Ein Körper ist auf seiner Weltlinie immer bei der Koordinate \(x = 0\). Eine Gerade mit dieser Eigenschaft stellt die Zeitachse dar, wobei die Richtung der Zeit vereinbarungsgemäß im Minkowski-Diagramm nach oben verläuft. Beispielsweise ist die Zeitachse im Außensystem die \(ct_a\)-Achse und die Zeitachse in Neles Bezugssystem ist mit \(x_n\) markiert.
b) Wir erläutern die Darstellung im bewegten Bezugssystem mit einem Beispiel: Ein Bezugssystem \(\text{B}_a\) hat die Achsen \(x_a\) und \(ct_a\), mit der Einheit\( c\cdot \text{s}\) auf jeder Achse. Ein Bezugssystem \(\text{B}_0\) hat die Achsen \(x_0\) sowie \(ct_0\) und bewegt sich relativ zu \(\text{B}_a\) mit einer Geschwindigkeit \(v\). Ein im Ursprung ausgesendeter Lichtblitz erreicht den Punkt B zur Zeit \(ct_a = 9\,c \cdot\text{s}\) in \(\text{B}_a\) und zur Zeit \(ct_B\) in \(\text{B}_0\).
Wenn ein in \(\text{B}_0\) ruhender Beobachter auf seiner Uhr die Zeit \(ct_B\) abliest, dann gilt für die gemäß der Zeitdilatation entsprechende Zeit \(ct_a\): \(ct_a = ct_B \cdot 𝛾 = ct_B\cdot \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\).
.
Der Punkt, an dem dieses Ablesen stattfindet, ist in \(B_0\) der Punkt \((x;\, ct) = (0;\, ct_B)\) und in \(\text{B}_a\) der Punkt \((x;\, ct) = (4 c \cdot\text{s};\, 5 c \cdot \text{s})\). In \(\text{B}_a\) hat das Ereignis des Ablesens bei \((4 c \cdot s;\, 5 c \cdot \text{s})\) eine Entfernung \(d\) vom Ursprung. Diese Entfernung ist gleich der Koordinate \(ct_B\) multipliziert mit einer noch unbekannten Einheit \(e_0\).
c) In Ba ist das Ereignis des Ablesens bei \((x_a;\, ct_a)\). Also gilt für das Quadrat der Entfernung vom Ursprung: \(𝑑^2 = (𝑐𝑡_a )^2 + 𝑥_a^2\). Entsprechend Teilaufgabe b) ist \(d^2\) das Quadrat aus der Koordinate \(ct_B\) multipliziert der Einheit \(e_0\): \(𝑑^2 = (𝑐𝑡_B \cdot 𝑒_0)^2 = (𝑐𝑡_a )^2 + 𝑥_a^2\)
d) Bei der hier betrachteten gleichförmigen Bewegung gilt: \(x_a = v \cdot t_a\).
e) Wir setzen in die Gleichung aus Teil c) die Gleichung aus Teil d) sowie Zeitdilatation aus Teil b) ein:
\((𝑐𝑡_B \cdot 𝑒_0 )^2 = (𝑐𝑡_a )^2 + 𝑥_𝑎^2 = (𝑐𝑡_B\cdot 𝛾)^2 + v^2 \cdot 𝑡_a^2= (𝑐𝑡_B\cdot 𝛾)^2 + v^2\cdot 𝑡_b^2\cdot 𝛾^2\)
Wir dividieren durch \(ct_b\) und erhalten:
\(𝑒_0^2 = 𝛾^2 +\frac{𝛾^2 \cdot v^2}{𝑐^2} = 𝛾^2\cdot \left(1 +
\frac{v^2}{c^2}\right)\).
Zeitdilatation und Längenkontraktion
Aufgabe 1
a) Zeitdilatation: Das Zeitintervall zwischen zwei Ereignissen ist im Eigensystem eines bewegten Objektes am kleinsten und im Außensystem gedehnt, die Zeit im Eigensystem vergeht dilatiert (langsamer). Das heißt, zwischen den zwei Ereignissen, z. B. „Aussenden eines Lichtstrahls“ und „Empfangen des reflektierten Lichtstrahls“ vergeht im Außensystem mehr Zeit als im Eigensystem. Daher schreitet zwischen diesen beiden Ereignissen der Zeiger einer Uhr im Außensystem weiter voran als der Zeiger einer Uhr im Eigensystem.
Längenkontraktion: Für bewegte Beobachter messen in Bewegungsrichtung eine kontrahierte (verkürzte) Laufzeitentfernung. Die Länge von Objekten schient also in Bewegungsrichtung verkürzt.
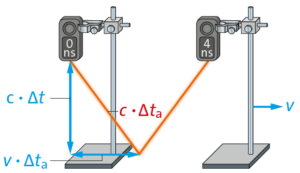
b) Zeitdilatation (vgl. S. 119):
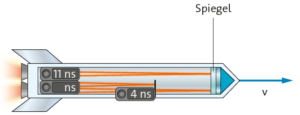
Längenkontraktion (vgl. S. 120):
c) Zeitdilatation: Bei einer Lichtuhr läuft das Licht in einem Zeitintervall \(Δt\) von der Uhr zum Spiegel und zurück. Im Eigensystem ist der Lichtweg \(c \cdot Δt\) . Im Außensystem \(a\) ist die Laufzeit \(Δt_a\) und der Lichtweg \(c \cdot Δt_a\) , wenn die Uhr einen Weg \(v \cdot Δt_a\) zurücklegt. Über das rechtwinklige Dreieck in der Abbildung aus Teilaufgabe b) erhält man die Formel für die Zeitdilatation:
\(\Delta t=\Delta t_a\cdot\sqrt{1-\frac{v^2}{c^2}\Rightarrow \Delta t_a=\gamma\cdot\Delta t}\) mit \(\gamma=\frac{1}{1-\frac{v^2}{c^2}}\)
Längenkontraktion: Eine Lichtuhr an Bord einer Rakete der Länge \(L\) mit Laser-Entfernungsmesser und Spiegel bewegt sich nach rechts (s. Abbildung in Teilaufgabe b). Im Eigensystem der Uhr und im Außensystem breitet sich Licht mit c aus. In einem Zeitintervall \(Δt\) läuft das Licht von der Uhr zum Spiegel und zurück. Die Laufzeit im Eigensystem beträgt \(\Delta t=\frac{2\cdot L}{c}\). Die Laufzeit im Außensystem beträgt \(L_a=\frac{\Delta t_a}{2}\cdot\frac{c^2-v^2}{c}=\frac{\Delta t_a\cdot c}{2\gamma^2}=\frac{L}{\gamma}\). Darauf ergibt sich die Längenkontraktion: \(L_a=\frac{L}{\gamma}=L\cdot\sqrt{1-\frac{v^2}{c^2}}\)
Aufgabe 2
a) Im Beschleuniger hat ein Myon stets eine hohe Geschwindigkeit \(v\) relativ zum Beobachter. Die Halbwertszeit in der Eigenzeit \(Δ𝑡\) des Myons ist eine Teilcheneigenschaft und bleibt unverändert. Der Beobachter stellt aufgrund der hohen Geschwindigkeit \(v\) eine deutlich verlängerte Halbwertszeit \(Δ𝑡_a\) im Außensystem fest.
b) Die Relation zwischen der Eigenzeit und der Zeit im Außensystem ist wie folgt:
\(Δ𝑡 = \sqrt{1 − \frac{v^2}{c^2}} \cdot Δ𝑡_a\)
Auflösen ergibt: \(v = 𝑐 \cdot \sqrt{1-\frac{\Delta t^2}{\Delta t_a^2}} = 299850\,\frac{\rm km}{\rm s}\)
Aufgabe 3
a) Die maximal mögliche Geschwindigkeit ist die Lichtgeschwindigkeit. Mit dieser Geschwindigkeit beträgt die Strecke beträgt \(𝑠 = 𝑐 \cdot Δ𝑡 = 456\,{\rm m}\).
b) Die Strecke ist zwar sehr kurz, aber aufgrund der Zeitdilation ist die Halbwertszeit für den ruhenden Beobachter deutlich vergrößert.
c) Die Relation zwischen der Eigenzeit und der Zeit im Außensystem ist wie folgt: \(Δ𝑡 = Δ𝑡_a\cdot \sqrt{1 − \frac{v^2}{c^2}}\)
Auflösen und einsetzen ergibt die beobachtete Halbwertszeit: \(Δ𝑡_a = \Delta t/\sqrt{1 − \frac{v^2}{c^2}}=53,7\,{\rm µs}\)
Die Myonen legen während \(Δ𝑡_a\) folgende Strecke zurück: \(𝑠 = v \cdot Δ𝑡_a = 16,117\,{\rm km} \approx 16\,{\rm km}\)
d) Die Myonen durchfliegen die Strecke von ihrer Entstehung zum Boden in weniger als einer beobachteten Halbwertszeit. Also kommen viele Myonen am Boden an.
Relativistische Masse und Energie
Aufgabe 1
a) Ein Elektron hat in Form seiner Ruhemasse 𝑚0 folgende Ruheenergie: \(𝐸_0 = 𝑚_0 \cdot 𝑐^2 = 0,5117\,{\rm MeV}\). Die kinetische Energie ist entsprechend der Energieerhaltung gleich der elektrischen Energie: \(𝐸_{\rm kin} = e \cdot U = 5\,{\rm MeV}\). Die Gesamtenergie ist gleich der Summe aus Ruheenergie und kinetischer Energie: \(𝐸 = 𝐸_0 + 𝐸_{\rm kin} = 5,5117\,{\rm MeV}\). Die relativistische Masse ist gleich dem Quotienten aus der Gesamtenergie und dem Quadrat der Lichtgeschwindigkeit: \(𝑚_a =\frac{𝐸}{c^2} = 9,812 \cdot 10^{−30}\,{\rm kg}\).
Die Relation zwischen der Eigenmasse oder Ruhemasse und der Masse im Außensystem oder der relativistischen Masse ist wie folgt: \(𝑚_0 = \sqrt{1 − \frac{v^2}{c^2}}\cdot 𝑚_a\). Auflösen ergibt \(v= 𝑐 \cdot\sqrt{1-\frac{m_0^2}{m_a^2}}= 298 704\,\frac{\rm km}{\rm s}\).
Der Impuls beträgt im Außensystem: \(𝑝_a = 𝑚_a \cdot v = 2,93 \cdot 10^{−21}\,\frac{\rm kg\cdot m}{\rm s}\)
b) Ein Proton hat in Form seiner Ruhemasse \(𝑚_0\) folgende Ruheenergie: \(𝐸_0 = 𝑚_0 \cdot 𝑐^2 = 939,6\,{\rm MeV}\). Die kinetische Energie ist entsprechend der Energieerhaltung gleich der elektrischen Energie: \(𝐸_{\rm kin} = e\cdot 𝑈 = 5\,{\rm MeV}\).
Die Gesamtenergie ist gleich der Summe aus Ruheenergie und kinetischer Energie: \(𝐸 = 𝐸_0 + 𝐸_{\rm kin} = 944,6\,{\rm MeV}\). Die relativistische Masse ist gleich dem Quotienten aus der Gesamtenergie und dem Quadrat der Lichtgeschwindigkeit: \(𝑚_a =\frac{E}{c^2}= 1,6815 \cdot 10^{−27}\,{\rm kg}\).
Die Relation zwischen der Eigenmasse oder Ruhemasse und der Masse im Außensystem oder der relativistischen Masse ist wie folgt: \(𝑚_0 = m_a\cdot \sqrt{1 − \frac{𝑣^2}{𝑐^2}}\)
Auflösen ergibt: \(v = 𝑐 \cdot \sqrt{1-\frac{m_0^2}{m_a^2}} = 30\,827\,\frac{\rm km}{\rm s}\)
Der Impuls beträgt im Außensystem: \(𝑝_a = 𝑚_a \cdot v = 5,18 \cdot 10^{−20}\,\frac{\rm kg\cdot m}{\rm s}\)
c) Die Relation zwischen der Eigenmasse oder Ruhemasse und der Masse im Außensystem oder der relativistischen Masse ist wie folgt: \(𝑚_0 = \sqrt{1 − m_a\cdot\frac{v^2}{c^2}}\)
Auflösen und einsetzen ergibt: \(𝑚_a = 𝑚_0/\sqrt{1 − \frac{v^2}{c^2}}=m_0/\sqrt{1-0,9^2}=3,837\,{\rm kg}\)
Die entsprechende Gesamtenergie ist das Produkt aus dieser Masse und dem Quadrat der Lichtgeschwindigkeit: \(𝐸 = 𝑚_a \cdot 𝑐^2 = 2156\,{\rm MeV}\)
Die kinetische Energie ist die Differenz aus der Gesamtenergie und der Ruheenergie: \(𝐸_{\rm kin} = 𝐸 − 𝐸_0 = 2155,6\,{\rm MeV} − 939,6\,{\rm MeV}= 1216\,{\rm MeV}\)
Die Beschleunigungsspannung beträgt somit \(𝑈 =\frac{𝐸_{\rm kin}}{𝑒}= 1216\,{\rm MV}\).
Aufgabe 2
a) Eine mögliche Versuchsskizze ist wie folgt, alternativ können Elektronen aus einem Beta-Strahler verwendet werden. In der Abbildung fliegen die Elektronen von links in den Geschwindigkeitsfilter mit der magnetischen Flussdichte \(B_1\) und gelangen anschließend in den analysierenden Bereich mit der magnetischen Flussdichte \(B_2\).
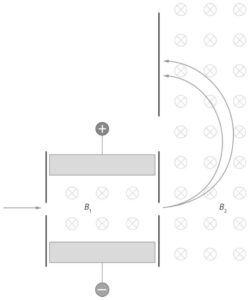
b) Der Lorentz-Faktor beträgt \(\gamma=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\), die Energie beträgt \(E=m\cdot c^2\).
| \(v/c\) | \(m\ \text{in}\ 10^{-30}\ \text{kg}\) | \(\gamma\) | \(E\ \text{in keV}\) |
| 0,3787 | 0,9835 | 1,0805 | 552,47 |
| 0,4281 | 1,0080 | 1,1065 | 566,23 |
| 0,5154 | 10,630 | 1,1669 | 597,13 |
| 0,6780 | 1,2380 | 1,3604 | 695,43 |
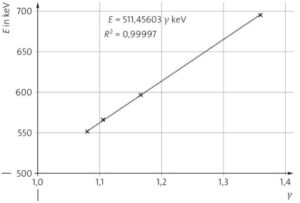
c) Entsprechend der Relativitätstheorie sollte die Energie proportional zum Lorentz-Faktor sein. Die folgende Abbildung zeigt die lineare Regression durch \((γ|𝐸) =(1|511\,{\rm keV})\).
d) Bei der linearen Regression durch \((γ|𝐸) =(1|511\,{\rm keV})\) gibt es nur einen Parameter, den Proportionalitätsfaktor 511,456 keV. Dieser ist die Energie bei der Geschwindigkeit null. Er stellt also die Eigenenergie oder Ruheenergie \(E_0\) des Elektrons dar. Die entsprechende Ruhemasse oder Eigenmasse des Elektrons beträgt entsprechend \(𝑚 =\frac{𝐸}{𝑐^2} = 9,1049 \cdot 10^{−31}\,{\rm kg}\). Die allgemeine lineare Regression ergibt einen weiteren Parameter, den \(y\)-Achsenabschnitt: Der \(y\)-Achsenabschnitt ist relativ klein und sollte null sein.
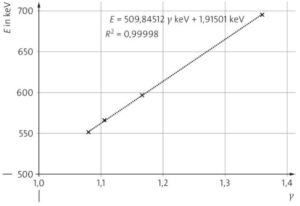
e) Die Beschreibung durch die Relativitätstheorie ist relativ genau, da das Quadrat des Korrelationskoeffizienten bei \(R^2 = 0,99997\) liegt. Die Bestimmung der Ruhemasse des Elektrons ergibt \(𝑚 = 9,1049 \cdot 10^{−31}\,{\rm kg}\). Der Literaturwert beträgt \(𝑚 = 9,109 \cdot 10^{−31}\,{\rm kg}\). Die Abweichung beträgt somit \(\frac{\Delta m}{m}= 0,045\,\%\).
Aufgabe 3
a) Beim Auftreffen der Elektronen auf die Elektrode werden Gammaquanten freigesetzt. Diese haben eine Energie von \(𝐸_\gamma =2,228\,{\rm MeV}\), wenn die Neutronen freisetzende Reaktion beginnt. Das zeigt die Abbildung. Bei der Neutronen freisetzenden Reaktion reagieren ein Deuterium \(^2_1\text{H}\) und ein Gammaquant\(gamma\) zu einem Proton p und einem Neutron \(\text{n}\). Die Reaktionsgleichung ist somit wie folgt: \(^2_1\text{H}+\gamma\rightarrow \text{p}+\text{n}+\text{e}\)
b) Die Ruheenergie von Deuterium beträgt \(𝐸_{\rm d} = 1876,1239\,{\rm MeV}\). Die Ruheenergie des Wasserstoffisotops \(^1_1\text{H}\) beträgt \(𝐸_1 = 938,784\,{\rm MeV}\). Der Reaktionsgleichung entspricht die folgende Energiegleichung: \(𝐸_{\rm d} + 𝐸_γ = 𝐸_1 + 𝐸_{\rm n}\)
c) Auflösen ergibt die Energie des Neutrons: \(E_{\rm n}=E_{\rm d}+E_\gamma-E_1=939,568\,{\rm MeV}\)
Aufgabe 4
a) Bei der Bewegung einer Ladung \(q\) mit einer Geschwindigkeit \(v\) senkrecht zu einer magnetischen Flussdichte \(B\) tritt die Lorentzkraft senkrecht zu \(v\) und \(B\) auf: \(𝐹_L = 𝑞 \cdot 𝑣 \cdot 𝐵\). Dabei entsteht eine Kreisbahn, bei der die Lorentzkraft gleich der Zentripetalkraft ist: \(𝐹_Z = 𝑚 \cdot 𝑣 \cdot 𝜔 = 𝐹_L\)
b) Eine auf eine frei bewegliche Masse wirkende Kraft \(F\) bewirkt die zeitliche Ableitung des Impulses \(\dot p = 𝐹\). Das gilt entsprechend dem zweiten Newtonschen Axiom (Grundprinzip der Mechanik).
c) Bei der Kreisbewegung wirkt die Kraft senkrecht zur Geschwindigkeit. Dadurch bleibt der Betrag der Geschwindigkeit unverändert. Somit bleibt die Masse 𝑚a konstant. Daher beträgt die Ableitung entsprechend der Produktregel: \(\dot p= 𝑚_a \cdot \dot v\)
d) Bei der Kreisbewegung ist der Radius konstant. Da auch die Geschwindigkeit konstant ist, ist zudem die Kreisfrequenz unveränderlich. Daher gilt für die Bahngeschwindigkeit \(v = r \cdot ω\). Eine Änderung der Geschwindigkeit kann also nur vektoriell erfolgen. Dazu schreiben wir die Geschwindigkeitskomponenten einzeln auf:
\(v_𝑥 = 𝑣 \cdot \cos (𝜔 \cdot 𝑡)\)
\(v_y = 𝑣 \cdot \sin (𝜔 \cdot 𝑡)\)
Wir leiten ab:
\(\dot v_𝑥 = -𝑣 \cdot \omega \cdot\sin (𝜔 \cdot 𝑡)\)
\(\dot v_y = 𝑣 \cdot \omega\cdot \cos (𝜔 \cdot 𝑡)\)
Wir bilden mit dem Satz des Pythagoras den Betrag der Ableitung: \(| \dot v | = 𝑣\cdot 𝜔\)
e) Mit \(|\dot v| = 𝑣 \cdot 𝜔\) aus Teilaufgabe d) ergibt sich die Ableitung des Impulses zu: \(\dot p = 𝑚_a \cdot \dot v = 𝑚_a \cdot 𝑣 \cdot 𝜔 = 𝐹_L = 𝑞 \cdot 𝑣 \cdot 𝐵\)
f) Wir lösen die Ableitung des Impulses aus Teilaufgabe e) nach der Kreisfrequenz auf und erhalten: \(\omega=q\cdot \frac{B}{m_a}\) oder \(f=q\cdot\frac{B}{2\pi\cdot m_a}\)
Allgemeine Relativitätstheorie
Aufgabe 1
a) Unten ist die Zeit entsprechend der Schwarzschild-Metrik verkürzt: \(𝑡_{\rm Erdboden} = 𝑡_\infty \cdot\sqrt{1 − \frac{𝑅_S}{𝑅_E}}\)
Dabei ist der Erdradius \(𝑅_E = 6371\,{\rm km}\) und die Erdmasse \(𝑀_E = 5,972 \cdot10^{24}\,{\rm kg}\). Der Schwarzschild-Radius der Erde beträgt \(𝑅_S =\frac{2𝐺\cdot 𝑀_E}{c^2}= 8,857\,{\rm mm}\). Einsetzen ergibt: \(𝑡_{\rm Erdboden} = 24\,{\rm h} \cdot\sqrt{1 −\frac{\rm 8,857\,mm}{6371\,km}}\)
Berechnen ergibt: \(𝑡_{\rm Erdboden} = 24\,{\rm h} − 60,06\,{\rm μs}\)
b) Einsetzen ergibt: \(𝑡_{\rm H} = 24\,{\rm h} \cdot\sqrt{1 −\frac{\rm 8,857\,mm}{\rm 26571\,km}}\)
Berechnen ergibt: \(𝑡_{\rm H} = 24\,{\rm h} − 14,40\,{\rm μs}\)
c) Der Zeitunterschied beträgt: \(\Delta t=t_{\rm H}-𝑡_{\rm Erdboden} =45,66\,{\rm μs}\)
In dieser Zeit legt Licht folgende Strecke zurück: \(\Delta s=\Delta t\cdot c=13,7\,{\rm km}\)
Die Bedeutung des Zeitunterschieds kommt wie folgt zustande: Beim GPS wird die Position des Nutzers ermittelt, indem Laufzeiten elektromagnetischer Wellen ermittelt werden, die von GPS-Satelliten zum Nutzer propagieren. Dazu übermittelt die Welle unter anderem den Zeitpunkt beim Start im Satelliten. Nun geht die Uhr im Satelliten aber schneller als eine Uhr auf der Erde. Würde man das nicht berücksichtigen, so würden sich die Laufzeitfehler nach einem Tag schon zu \(Δ𝑡 = 45,66\,{\rm μs}\) akkumulieren. Die Laufzeit wird mit der Lichtgeschwindigkeit multipliziert, um die Position zu ermitteln. Also könnte bereits nach einem Tag ein Streckenfehler von \(13,7\,{\rm km}\) entstehen. Selbstverständlich wird der Zeitunterschied rechnerisch ausgeglichen.
Aufgabe 2
a) Wir wenden die Relation \(c=f\cdot \lambda\) an. Somit beträgt die Wellenlänge \(\lambda_H=\frac{c}{f_H}=0,1347\,{\rm m}\). Wir wenden die Relation der Wellenlängen an: \(\lambda(r)=\epsilon(r)\cdot\lambda_\infty\). Wir lösen nach der Wellenlänge beim Abstand \(r\) gegen unendlich auf und erhalten. \(\lambda_\infty=\frac{\lambda(r)}{\epsilon(r)}\). Für \(r_H\) ist dann \(\lambda_\infty=\frac{\lambda(r_H)}{\epsilon(r_H)}\).
Wir wenden die erste Gleichung für den Erdboden an: \(\lambda(r_E)=\epsilon(r_E)\cdot\lambda_\infty\). Wir setzen den obigen Ausdruck für \(\lambda_\infty\) ein und erhalten \(\lambda(r_E)=\epsilon(r_E)\cdot\frac{\lambda(r_H)}{\epsilon(r_H)}\).
Wir wenden die Relation \(\epsilon(r)=\sqrt{1-R_S/r}\) an: \(\lambda(r_E)=\lambda(r_H)\cdot\sqrt{\frac{1-R_S/R_E}{1-R_S/R_H}}\)
Einsetzen von \(R_E=6371\,{\rm km}\), \(R_S=8,857\,{\rm mm}\) und \(R_H=26571\,{\rm km}\) sowie \(\lambda_H=0,1347\,{\rm m}\) ergibt: \(\lambda(r_E)=\lambda(r_H)\cdot\sqrt{\frac{1-R_S/R_E}{1-R_S/R_H}}=\lambda(r_H)-71,2\,{\rm pm}\)
b) Die Wellenlänge ist unten kürzer. Daher ist die Energie des Photons unten größer. Denn auf dem Weg von oben nach unten hat das Photon Energie der Lage in lokal messbare Energie des Photons \(𝐸_{\rm Photon} =ℎ \cdot \frac{c}{\lambda}\) umgewandelt.
c) Beim Sender beträgt die Energie: \(𝐸_{\rm Photon,\,H} =ℎ \cdot \frac{c}{\lambda_H}=1,476\cdot 10^{-24}\,{\rm J}\)
Beim Empfänger beträgt die Energie: \(𝐸_{\rm Photon,\,E,} =ℎ \cdot \frac{c}{\lambda_g}=E_{\rm Photon,\,H}+7,8\cdot 10^{-34}\,{\rm J}\)
Anwendungen der Relativitätstheorie
Aufgabe 1
a) Wir berechnen:
\(E = 512\,{\rm keV }+ 20\,{\rm MeV}= 20,512\,{\rm MeV}\)
\(m = \frac{E}{c^2}= 3,651 \cdot 10^{–29}\,{\rm kg}\)
\(γ = \frac{E_0}{E} = 40,0625\)
\(v=c\cdot \sqrt{1-\gamma^2} = 299 907\,\frac{\rm km}{\rm s}\)
\(p = m_0 \cdot γ \cdot v= 4.387 \cdot 10^{–19}\,\frac{\rm kg \cdot m}{\rm s}\)
b) Die Äquivalenz von Masse und Energie \(E=m\cdot c^2\) bedeutet, dass mit der Geschwindigkeit auch die Energie und damit die relativistische Masse des Teilchens steigt. Diese ergibt sich aus der Ruhemasse \(m_0\) und dem Lorentzfaktor \(\gamma=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\) zu \(m=m_0\cdot\gamma\).
c) Wir setzen die Ausdrücke für Lorentzkraft und Zentripetalkraft gleich: \(F_L=F_Z\Rightarrow B\cdot v\cdot e=\frac{m\cdot v^2}{r}=\frac{p\cdot v}{r}\). Daraus folgt: \(r=\frac{p}{B\cdot e}=0,55\,{\rm m}\)
d) Die größte Energie und damit die kleinste Wellenlänge entsteht, wenn die gesamte kinetische Energie der Elektronen in die Energie des Photons übertragen wird:\(E_{\rm kin}=E_{\rm Photon}=\frac{h\cdot c}{\lambda}\). Daraus folgt: \(\lambda=\frac{h\cdot c}{E_{\rm kin}}=\frac{h\cdot c}{\rm 200\,MeV}=62\,{\rm fm}\)
e) Für die Betrachtung des relativistischen Effektes der Zeitdilatation müssen wir den Prozess im Eigensystem und Außensystem betrachten: Der Lorentzfaktor ergibt sich zu \(\gamma=\frac{E_0}{E}=5,717\). Daraus lässt sich die Geschwindigkeit ermitteln: \(v=c\cdot\sqrt{1-\gamma^2}=295\,375\,\frac{\rm km}{\rm s}\)
Im Außensystem ergibt sich die Flugzeit \(t_a=\frac{s}{v}=91,4\,{\rm µs}\) und im Eigensystem \(t=\frac{t_a}{\gamma}=16\,{\rm µs}\). Im Eigensystem der Myonen vergeht also weniger Zeit, die Zeit vergeht langsamer (Zeitdilatation).
Für den Anteil der zerfallenen Myonen in der ruhenden Probe (Außensystem) ergibt sich: \(\frac{N_a}{N_0}=\left(\frac{1}{2}\right)^{\frac{t}{t_H}}=7,9\cdot 10^{-19}\)
Im Eigensystem der Myonen ergibt sich \(\frac{N}{N_0}=\left(\frac{1}{2}\right)^{\frac{t}{t_H}}=6,8\cdot 10^{-4}\). In der ruhenden Probe sind also deutlich mehr Myonen zerfallen.
Aufgabe 2
a) Wenn sich der Laserkreisel in der Abbildung wie dargestellt dreht, dann legen die beiden rot dargestellten Lichtwellen unterschiedlich lange Wege bis zum Interferieren zurück. Das ist im Interferenzbild erkennbar.
b) Das Licht benötigt für einen Umlauf im Ring die Zeit \(\text{d}𝑡 =\frac{2𝜋\cdot 𝑟}{𝑐}\). Wir analysieren exemplarisch einen Wellenberg, der sich beim Eintritt in den Ring in der Abbildung erstenteils nach oben und zweitenteils nach unten ausbreitet. Dem ersten Teil kommt der Ausgang mit der Bahngeschwindigkeit \(𝑣 = 𝜔 \cdot 𝑟\) entgegen. Während der Zeit \(\text{d}t\) verkürzt sich der Weg für den ersten Teil um den Weg \(Δ𝑠_1 = 𝜔 \cdot 𝑟 \cdot \text{d}𝑡\).
Während dieser Zeit \(\text{d}t\) verlängert sich der Weg für den zweiten Teil um den gleichen Weg \(Δ𝑠_2 = 𝜔 \cdot 𝑟 \cdot \text{d}𝑡\). Der Wegunterschied beider Teile ist also die Summe: \(Δs = Δ𝑠_1 + Δ𝑠_2 = 2𝜔 \cdot 𝑟 \cdot \text{d}𝑡\). Wir wenden den obigen Term für \(\text{d}t\) an: \(Δs = 2𝜔 \cdot 𝑟 \cdot\frac{2𝜋\cdot 𝑟}{𝑐}=\frac{4𝜔}{𝑐}\cdot 𝜋𝑟^2 =\frac{4𝜔\cdot 𝐴}{𝑐}\).
c) Das Maximum der Giergeschwindigkeit in der Abbildung beträgt: \(\omega=40\,\frac{\rm Grad}{\rm s}=\frac{40}{\rm 180\,s}\cdot\pi=\frac{2\pi}{\rm 9\,s}\)
Wir ermitteln den Wegunterschied mit dem obigen Term: \(Δs =\frac{4𝜔}{𝑐}\cdot 𝜋𝑟^2 = 2,92 \cdot 10^{−10}\,{\rm m}\)
Der entsprechende Phasenunterschied beträgt im Bogenmaß: \(Δ𝜙 =\frac{Δs}{𝜆}\cdot 2𝜋 = 3,67 \cdot 10^{−3}\)
Wenn die beiden Lichtwellen durch eine Glasfaser propagieren, die den Ring in der Abbildung mehrfach durchläuft, dann multipliziert sich der Wegunterschied und somit ebenso der Phasenunterschied mit der Anzahl dieser Umläufe. Der Sensor wird dann auch Faserkreisel genannt.
d) Entsprechend der Relativitätstheorie kann man die Geschwindigkeit eines Körpers nur relativ zu einem Objekt messen, nicht jedoch relativ zum Raum.
Dagegen kann ein Sensor Beschleunigungen messen, wobei der Sensor aber Beschleunigung und Gravitation prinzipiell nicht lokal unterscheiden kann. In dieser Weise beschreibt die Relativitätstheorie die Möglichkeiten und Grenzen lokaler Sensoren zur autonomen Navigation.
© Cornelsen Verlag GmbH, Berlin