Lösungen zum Check-up 8: Strahlung und Materie – Cornelsen

Entstehung von Röntgenstrahlung

Aufgabe 1

Aufgabe 2

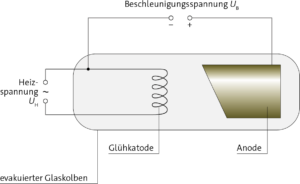
Merkmale: Röntgenstrahlung entsteht, wenn hochenergetische Elektronen auf ein Anodenmaterial mit hoher Kernladungszahl (viele Protonen) treffen. Dabei entsteht Bremsstrahlung und für das Anodenmaterial charakteristische Strahlung mi \(\lambda<10\,{\rm nm}\). Röntgenstrahlung durchdringt bestimmte Arten von Materie und wechselwirkt mit anderen. Deshalb werden mit ihr z. B. Knochenstrukturen über ein Absorptionsmuster untersucht.

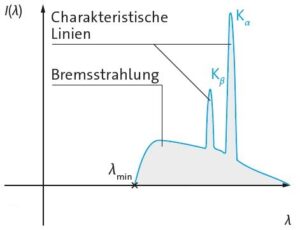
Entstehung von Bremsstrahlung: Wenn die Elektronen auf die Anode treffen, werden sie an den Protonen der Kerne stark abgebremst bzw. abgelenkt und geben Bremsstrahlung ab. Die maximale Energie der Strahlung ist \(E = h \cdot f = h \cdot\frac{c}{\lambda}\) und kann nicht größer sein als die kinetische Energie der abgebremsten Elektronen \(E = e \cdot U_{B}\). Deshalb gibt es eine minimale Wellenlänge der Röntgenstrahlung (s. Skizze des Spektrums).

Entstehung von charakteristischer Strahlung: Außer der Bremsstrahlung gibt es auch die für ein Anodenmaterial charakteristische Röntgenstrahlung. Sie entsteht, wenn ein schnelles Elektronen ein kernnahes Elektron aus einem der Atome des Anodenmaterials stößt und dann ein Elektron aus einem höheren Energieniveau nachrückt. Wird ein Elektron aus der K-Schale \((n = 1)\) eines Atoms entfernt und die Lücke durch Nachrücken eines Elektrons von einem höheren Energieniveau (\(n = 2\) oder \(n = 3\)) aufgefüllt, entsteht Kα bzw. Kβ-Strahlung. Die Kα-Strahlung \((n = 2 \rightarrow 1)\) besitzt weniger Energie (größere Wellenlänge \(λ\) ), ist aber wahrscheinlicher und damit häufiger als die Kβ-Strahlung. Deshalb ist der Peak der Kα-Strahlung höher, liegt aber weiter rechts im Spektrum.

Aufgabe 3

\(e\cdot U_B=E_{\rm ph}=h \cdot\frac{c}{\lambda} \Rightarrow U_B=\frac{h\cdot c}{e\cdot \lambda}=2,5\cdot 10^5\,{\rm eV}=250\,{\rm keV}\)

Röntgenspektroskopie

Aufgabe 1

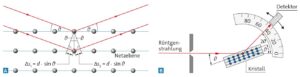
a) Trifft Röntgenstrahlung auf ein Material mit einer regelmäßigen Kristallstruktur, so regt sie die Elektronen zur Aussendung von Strahlung gleicher Frequenz an. Von den Atomen gehen entsprechend dem Huygensschen Prinzip neue Elementarwellen aus. Dabei tritt in der Richtung konstruktive Interferenz auf, für die der Reflexionswinkel gleich dem Einfallswinkel ist. Im Kristall kommt es zur Reflexion an mehreren parallelen Gitterebenen (A). Wellen, die an benachbarten Netzebenen reflektiert werden, haben dabei einen Gangunterschied von \(\Delta s = 2d \cdot \sin (\vartheta )\). Für den Glanzwinkel ϑ ist zugleich die Bedingung \(Δs = nλ\) der konstruktiven Interferenz erfüllt. Durch die Messung des Glanzwinkels über die Drehkristallmethode kann man mit der Bragg-Bedingung auf den Abstand von Netzebenen im Material schließen (B).

Variiert man also den Messwinkel \(\vartheta\), kann man für verschiedene Beschleunigungsspannungen \(U_B\) die Intensität messen. Darüber lässt sich dann im Intensitätsmaximum der Glanzwinkel bestimmen.

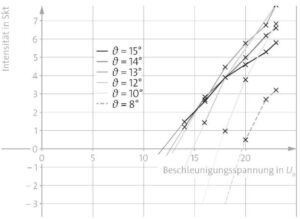
c) Die Schnittpunkte sind in der Grafik eingezeichnet:

Winkel in °	15	14	13	12	10	8
Schnittpunkte mit \(I=0\) in kV	11,9	12,6	13,1	14,8	17,4	19,8

d) Die Schnittpunkte geben die Beschleunigungsspannung an, ab der die vom LiF-Kristall beeinflusste Intensität der Röntgenphotonen zu beobachten ist. Es zeigt sich: Je kleiner der eingestellte Winkel des Kristalls ist, desto höher ist die Spannung. Nach der Bragg-Gleichung ist der eingestellte Winkel proportional zur Wellenlänge der Röntgenphotonen und damit ist die Wellenlänge der Photonen umso kürzer, je höher die Beschleunigungsspannung ist.
Der kleinste zu beobachtende Wert der Wellenlänge ergibt sich somit aus den Schnittpunkten.

e) Aus der Bragg-Gleichung \(2 \cdot d \cdot \sin ϑ = n \cdot λ\) erhält man die zu den jeweiligen Winkel gehörige Wellenlänge und aus \(c = \lambda\cdot f\) die Frequenz:

Winkel in °	15	14	13	12	10	8
\(f\) in \(10^{18}\) Hz	2,883	3,084	3,317	3,589	4,298	5,362
Schnittpunkte mit \(I=0\) in kV	11,9	12,6	13,1	14,8	17,4	19,8

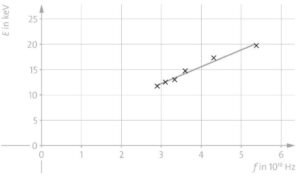
Die Werte im Diagramm liegen ungefähr auf einer Geraden, da sich die maximale Energie der Röntgenphotonen aus der Energie der beschleunigten Elektronen ergibt. Nach der Gleichung \(E = h \cdot f\) ergibt sich aus der Proportionalität von Frequenz und Energie in keV die Proportionalitätskonstante
\(h\) mit dem Wert des Plankschen Wirkungsquantums \(h = 3,296 \cdot 10^{–15}\,{\rm eV\,s}\). Der Literaturwert wird mit \(4,13566769692…\cdot 10^{–15}\,{\rm eV\,s}\) angegeben. Achtung: Messungenauigkeiten sind hier in der Auswertung nicht berücksichtigt.

Aufgabe 2

a) Ein Photon im sichtbaren Bereich hat eine Wellenlänge von 380 nm bis 780 nm. Die Energien gehen von 3,3 eV bis 1,6 eV. Ein Röntgenphoton mit 10 kV hat etwa die 5000-fache Energie.

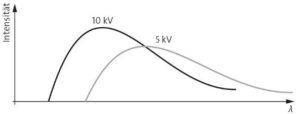
b) Die Elektronen in einer Röntgenröhre werden mit der Beschleunigungsspannung beschleunigt und haben alle etwa die gleiche Energie. Beim Abbremsen entstehen Röntgenphotonen. Ein Röntgenphoton hat dann die maximale Energie, wenn es mit der gesamten kinetischen Energie eines Elektrons erzeugt wird. Zu dieser maximalen Photonenenergie gehört eine minimale Wellenlänge, die Grenzwellenlänge.

c) Es gilt \(\lambda_G=\frac{h\dot c}{e\dot U}\).

Für \(U=5\,{\rm kV}\) erhält man: \(\lambda_G=2,50\cdot 10^{-10}\,{\rm m}=250\,{\rm pm}\)

Für \(U=10\,{\rm kV}\) erhält man: \(\lambda_G=1,25\cdot 10^{-10}\,{\rm m}=125\,{\rm pm}\)

Aufgabe 3

a) Um Knochen zu untersuchen, kann sehr harte Röntgenstrahlung verwendet werden, denn Knochen lassen sich auch bei harter Strahlung noch vom sonstigen Gewebe unterscheiden. Sollen Organe untersucht werden, muss die Strahlung weicher als \(1,5 \dot 10^{–14}\,{\rm J}\) sein, damit sich verschiedene Gewebearten (Muskeln, Fett) unterscheiden lassen.

b) Günstige Eigenschaften eines Kontrastmittels sind:
– absorbiert Röntgenstrahlung stark (geringe Durchdringung)
– reichert sich verstärkt in den untersuchten Organen an
– ist leicht zu verabreichen und gut verträglich (keine Nebenwirkungen)
– ist leicht herzustellen bzw. günstig einzukaufen.

Kernzerfälle

Aufgabe 1

a) Der Nuklidkarte ist zu entnehmen, dass die Silber-Isotope \(^{107}_{47}{\rm Ag}\) und \(^{109}_{47}{\rm Ag}\) stabil sind. Wir können davon ausgehen, dass die beiden stabilen Silber-Isotope in der Folie vorhanden sind. Bei der Bestrahlung mit langsamen Neutronen fangen die Silber-Atome die Neutronen ein. Dadurch erhöht sich ihre Massenzahl um 1. Es entstehen also \(^{108}_{47}{\rm Ag}\)und \(^{110}_{47}{\rm Ag}\).

b) Die beiden Tabellen zeigen die Zählraten zu unterschiedlichen Zeitpunkten. Für die Begründung nutzen wir die Halbwertszeiten von \(^{108}_{47}{\rm Ag}\)und \(^{110}_{47}{\rm Ag}\), welche auch im Ausschnitt der Nuklidkarte zu finden sind. Für \(^{110}_{47}{\rm Ag}\) beträgt die Halbwertszeit 24,6 s und für \(^{108}_{47}{\rm Ag}\) beträgt 147 s. In den ersten 30 Sekunden nach der Bestrahlung mit langsamen Neutronen wird also überwiegend die ausgesandte β-Strahlung von \(^{110}_{47}{\rm Ag}\) gemessen. Nach 300 Sekunden sind für \(^{110}_{47}{\rm Ag}\) aber schon mehr als 12 Halbwertszeiten vergangen. Es ist also von \(^{110}_{47}{\rm Ag}\) weniger als \(\left(\frac{1}{2}\right)^{12}\approx 0,025\,%\) vorhanden, so dass jetzt fast nur die ausgesandte β-Strahlung von \(^{108}_{47}{\rm Ag}\) gemessen wird.

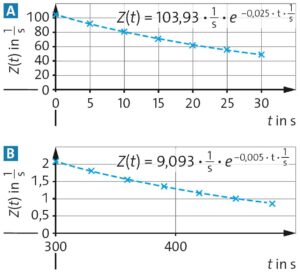
c) Diagramme und exponentielle Regression ergeben die funktionalen Zusammenhänge: \(Z(t) = 103,93\,\frac{1}{\rm s}\cdot \text{e}^{−0,025 \cdot  t\,\frac{1}{\rm s}}\) für \(t = 0–30\,{\rm s}\), also \(^{110}_{47}{\rm Ag}\) , und \(Z(t) = 9,093\,\frac{1}{\rm s}\cdot \text{e}^{−0,005 \cdot  t\,\frac{1}{\rm s}}\) für \(t = 300–480\,{\rm s}\), also \(^{108}_{47}{\rm Ag}\). Die Halbwertszeiten für \(^{108}_{47}{\rm Ag}\) und \(^{110}_{47}{\rm Ag}\) werden über \(λ = \frac{\ln(2)}{T_H}\) berechnet. Die durch die Messwerte ermittelten Halbwertszeiten betragen für \(^{108}_{47}{\rm Ag}\) ca. 28 s und für \(^{110}_{47}{\rm Ag}\) ca. 139 s. Abbildung A zeigt \(Z(t)\) für die ersten 30 Sekunden, Abbildung B für den Zeitraum 300 bis 480 Sekunden.

Aufgabe 2

Das Vorgängernuklid mit Alphazerfall ist \(^{84}_{210}{\rm Po}\) . Das Vorgängernuklid mit Betazerfall ist \(^{81}_{206}{\rm Tl}\).

Vermutung: Die Halbwertszeiten der Ausgangsnuklide der natürlichen Zerfallsreihen sind größer als das Alter der Erde. Begründung: Diese Ausgangsnuklide der Zerfallsreihen existieren noch. Wären die Halbwertszeiten kleiner als das Erdalter, müssten diese Zerfallsreihen heute „ausgestorben“ sein.

Nukleonen im Potenzialtopfmodell

Aufgabe 1

Wir gehen davon aus, dass die Kerne aus Protonen entstanden sind, die sich im frühen Universum gebildet haben. Beispielsweise ist der Kern zu \(^6{\rm B}\) aus sechs Protonen entstanden. Der Massendefekt \(Δm\) ist gleich der Masse der Produkte abzüglich der Masse der Edukte: \(Δm = m_{\rm Kern} – 6 \cdot m_p\)
Wir setzen für \(m_p = 1,007276467\,\text{u}\) ein und erhalten so folgende Tabelle. Die Tabelle stellt Massendefekte dar.

Kern	\(A\)	\(m\ \text{in u}\)	\(\Delta m\ \text{in u}\)
Bor-6	6	6,0480571	0,0043983
Bor-7	7	7,0269691	-0,02396617
Bor-8	8	8,0218644	-0,03634733
Bor-9	9	9,0105867	-0,0549015
Bor-10	10	10,0101941	-0,06257057
Bor-11	11	11,0065621	-0,07347903
Bor-12	12	12,0116097	-0,0757079
C-12	12	12	-0,0873176
He-4	4	4,00150618	-0,02759969

Aufgabe 2

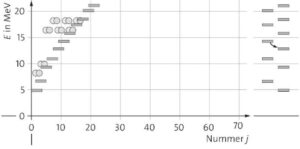
Die Abbildung stellt den energetisch günstigen Übergang von Bor-12 zu C-12 dar (Pfeil). Es handelt sich um einen β-Zerfall. Diese wird entsprechend der Nuklidkarte auch als natürlicher Zerfall beobachtet.

Aufgabe 3

Die Nuklidkarte zeigt, dass Bor-8 durch β+-Zerfall in Beryllium-8 zerfällt. Diese zerfällt in zwei Helium-4-Kerne. Die obige Tabelle zeigt, dass diese einen Massendefekt von \(Δm =2 \cdot (–0,0276\,\text{u}) = –0,055\,\text{u}\) haben. Das ist energetisch wesentlich günstiger als der Massendefekt von Bor-8 mit -0,036 u.

Ionisierende Strahlung

Aufgabe 1

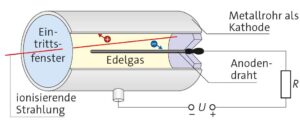
Aufgabe 2

Annahmen:

Die radioaktive Quelle strahlt in alle Richtungen gleichmäßig. Dann entsprechen alle Orte mit gleichem Abstand \(r\) zur Quelle einer Kugeloberfläche mit dem Inhalt \(4π \cdot r^2\).
Die „Strahlungsstärke“ entspricht der Menge der Strahlung, die auf eine bestimmte Fläche trifft. Für die doppelte Entfernung \(2r\) zur Quelle ergibt sich eine bestrahlte Fläche von \(4π \cdot (2r)^2 = 4 \cdot (4π \cdot r^2)\). Die bestrahlte Fläche ist also 4-mal so groß. Das heißt: Bei doppelter Entfernung „verdünnt“ sich die Strahlung auf \(\frac{1}{4}\) der Stärke.

Aufgabe 3

Alphastrahlung: Weg 2; Alphastrahlung trägt positive elektrische Ladung. Deshalb wird sie zur negativ geladenen Platte hin abgelenkt.

Betastrahlung: Weg 1 und Weg 4; Weg 4: 𝛽−-Strahlung trägt negative elektrische Ladung. Deshalb wird sie zur positiv geladenen Platte hin abgelenkt. Weg1: 𝛽+-Strahlung trägt positive elektrische Ladung. Deshalb wird sie zur negativ geladenen Platte hin abgelenkt. Beide Betastrahlungen sollten aber die gleiche Ablenkung, nur in andere Richtungen erfahren, da die 𝛽− und die 𝛽+-Strahlung aus Elektronen bzw. Positronen besteht, welche Antiteilchen zueinander sind.

Gammastrahlung: Weg 3; Gammastrahlung trägt keine elektrische Ladung. Deshalb wird sie im elektrischen Feld nicht abgelenkt.

Aufgabe 4

a) Die Nullrate muss nicht berücksichtigt werden, da beim Experiment ein Blatt Papier direkt vor dem Zählrohr positioniert wird. Dieses ist bei der Bestimmung der Nullrate nicht vorhanden. Das Blatt Papier wird vor dem Zählrohr positioniert, um die α-Strahlung abzuschirmen.

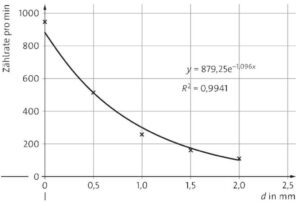
b) Aus dem Diagramm kann die ungefähre Halbwertsdicke \(d_H\) von 0,5 mm abgelesen werden. Bei genauerer Berechnung über: \(439,625 = 879,25 \cdot\text{e}^{-1,096 \cdot d\,\frac{1}{\rm m}}\) ergibt sich: \(d_H = 0,63\,{\rm mm}\).

c) Der Knopfstrahler enthält U-238, welches α-Strahlung aussendet. Diese α-Strahlung kann aber nicht durch die Ummantelung des Knopfstrahlers gelangen und auch nicht durch das Blatt Papier vor dem Zählrohr. Es handelt sich um einen β-Strahler, da die Strahlung durch Aluminium absorbiert werden kann.

d) Es ist für die Auswertung wichtig, dass der Knopfstrahler keine γ-Strahlung aussendet, da diese kaum durch Aluminium absorbiert werden kann. Die γ-Strahlung würde dann weiter von dem Zählrohr detektiert werden. Dadurch wäre keine Auswertung für die β-Strahlung möglich.