Atommodelle
Aufgabe 1
Das Bohrsche Atommodell eignet sich zur Beschreibung und Berechnung von Energieniveaus in Wasserstoffatomen.
Merkmale:
- Elektronen bewegen sich mit bestimmten Energien auf Kreisbahnen (Schalen) um den positiven aus Protonen bestehenden Kern.
- In den Bereichen zwischen den Bahnen befinden sich keine Elektronen.
- Höhere Bahnen (weiter vom Kern entfernt) sind energiereicher, haben also eine höhere Energiestufe.
- Beim Übergang zwischen verschiedenen Bahnen kann das Atom dann Energie aufnehmen oder abgeben.
Vorteile sind, dass man nach dem Bohrschen Modell bereits relativ genau die Energien von Elektronen und deren Übergängen bestimmen kann. Nachteile sind, dass das Modell nicht die feineren Energiezustände erklärt, die durch das Orbitalmodell beschrieben werden.
Aufgabe 2
Die Grenzen des Bohrschen Atommodells wurden vom Orbitalmodell beglichen. Heutzutage geht man davon aus, dass sich die Elektronen nicht auf Bahnen um den Kern bewegen. Stattdessen besitzen sie Antreffwahrscheinlichkeiten für bestimmte Bereiche im Atom, die durch Orbitale beschrieben werden. Die Elektronen sind nicht mehr lokalisiert, sondern nur mit einer bestimmten Wahrscheinlichkeit \(p(x)\) an einem bestimmten Ort \(x\) im Atom aufzufinden. Mit dem Orbitalmodell lassen sich Atomhülle und atomare Verbindungen beschreiben.
Spektrum des Wasserstoffs
Aufgabe 1
a)
| \(n\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| \(E_n\) in eV | -13,6 | -3,4 | -1,51 | -0,85 | -0,54 | -0,38 | -0,28 | -0,21 |
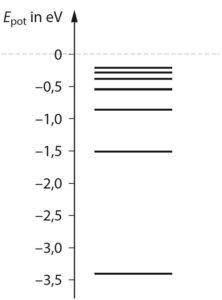
b) Die Niveaus zu liegen bei größeren n immer näher beisammen, was zunehmend schwieriger darzustellen ist.
c) Das erste Niveau mit \(E_1=-13,6\,{\rm eV}\) liegt 10,2 eV unterhalb des zweiten mit \(E_1=-3,4\,{\rm eV}\). Dies entspricht \(10,2\cdot 5\,{\rm cm}=51\,{\rm cm}\).
d) Sichtbares Licht liegt im Bereich von 0,38 μm bis 0,75 μm. Nur beim Übergang \(3 \rightarrow 2\) werden für das menschliche Auge wahrnehmbare Photonen ausgesendet.
| von | nach | \(\Delta E\) in eV | \(\lambda\) in µm |
| 2 | 1 | 10,20 | 0,12 |
| 3 | 2 | 1,89 | 0,66 |
| 4 | 3 | 0,66 | 1,9 |
| 5 | 4 | 0,31 | 4,0 |
| 6 | 5 | 0,17 | 7,5 |
| 7 | 6 | 0,10 | 12,0 |
| 8 | 7 | 0,065 | 19,0 |
Aufgabe 2
Die ersten Linien im UV-Bereich sind diejenigen, deren Wellenlängen kürzer als 400 nm sind, wobei die Linie mit \(\lambda = 397\,{\rm nm}\) für die meisten Menschen wohl noch sichtbar ist. Diese gehört zum Übergang von \(n_2 = 7\) auf \(n_1 = 2\). Zu berechnen sind also die Linien der Übergänge von \(n_2 = 8,\ 9,\ 10\) und 11 nach \(n_1 = 2\):
Mit der Formel \(\frac{1}{\lambda}=R_\text{H}\cdot\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\) und der Konstanten \(R_H= 1,096778 \cdot 10^{7}\,\frac{1}{\rm m}\) erhält man die gesuchten Wellenlängen:
\(n_2 = 8:\ \lambda = 389,02\,{\rm nm}\)
\(n_2 = 9:\ \lambda = 383,65\,{\rm nm}\)
\(n_2 = 10:\ \lambda = 379,90 \,{\rm nm}\)
\(n_2 = 11:\ \lambda = 38377,17 ,02\,{\rm nm}\)
Aufgabe 3
Berechnung mit der in 2) benutzten Formel: Für \(n_2 \rightarrow\infty\) wird der zweite Bruch in der Klammer unendlich klein. Für die Balmer-Serie mit \(n_1 = 2\) ergibt sich die Grenzwellenlänge zu \(\frac{1}{\lambda}=R\cdot 0,25\Rightarrow\lambda=364,70\,{\rm nm}\).
Mit \(c = \lambda \cdot f\) folgt daraus für die Grenzfrequenz \(f_{\rm Gr}= 8,218 \cdot 10^{14}\,{\rm Hz}\).
Aufgabe 4
Von den Gasen in der Erdatmosphäre wird ein Teil der Strahlung absorbiert, die von der Sonne stammt. Macht man auf der Erde eine Spektralanalyse des dort ankommenden Sonnenlichts, kann man deshalb schwarze Linien beobachten. Bestimmte Wellenlängen des Spektrums gelangen nicht bis zur Erdoberfläche, weil sie z. B. in der Atmosphäre absorbiert werden. Diese Absorptionslinien heißen Fraunhofersche Linien. Durch die Analyse dieser Linien kann man z. B. die in der Atmosphäre vorhandenen Atome identifizieren und damit die atomare Zusammensetzung bestimmen. So lassen sich die Spektrallinien von Natrium oder von Wasserstoff im Spektrum erkennen.
Aufgabe 5
a) Die waagerechten Linien mit den Bezeichnungen \(n = 1,\ n = 2\) usw. stellen die möglichen Energiestufen im Wasserstoff-Atom dar. Rechts stehen die Energien. Wird ein Atom durch Zuführen von Energie angeregt, so kann es diese Energie nur in bestimmten Beträgen, in „Quanten“, aufnehmen (Absorption) oder abgeben (Emission). Die senkrechten Pfeile stellen die möglichen Energieübergänge dar. Sie sind in Gruppen, den Spektralserien, zusammengefasst, je nachdem bei welchem unteren Energieniveau sie beginnen. Wird eine Energie größer als 13,6 eV zugeführt, so verlässt das Elektron die Atomhülle (Ionisation).
b) Die größte Wellenlänge ist die mit der kleinsten Energiedifferenz, die kleinste Wellenlänge die mit der größten. Grundlage für die Berechnung ist die Formel \(λ = \frac{h\cdot c}{ΔE}\).
Die kleinste Energiedifferenz bei der Balmer-Serie ist der Übergang von \(n = 3\) nach \(n = 2\), entsprechend \(\Delta E=-1,53\,{\rm eV}-(-3,41\,{\rm eV})=1,88\,{\rm eV}\). Umgerechnet in Joule erhält man \(3,01 \cdot 10^{–19}\,{\rm J}\). Eingesetzt in die Formel ergibt dies \(λ = 659\,{\rm nm}\).
Die größtmögliche Energiedifferenz der Paschen-Serie ist der Übergang von \(\infty\) auf \(n = 3\). Die Differenz von 1,53 eV ergibt \(λ = 810\,{\rm nm}\).
c) Mit der gegebenen Formel lässt sich die Energiedifferenz zwischen zwei Energieniveaus im Wasserstoff-Atom berechnen. Dabei sind \(n_1\) und \(n_2\) ganze Zahlen mit \(n_1,\ n_2 > 0\) und \(n_1 > n_2\). Außerdem sind \(e\) und \(h\) Naturkonstanten, \(f_R\) ist die Rydberg-Frequenz.
d) Bei der Ionisation wird das Elektron im Wasserstoff vom Grundzustand \(n = 1\) (ein Elektron in der Hülle) über den Zustand \(n=\infty\) gehoben. Einsetzen in die Formel ergibt 13,6 eV.
e) Für die Paschen-Serie ist \(n_1 = 3\). Einsetzen in die Formel aus c) ergibt \(\Delta E=\frac{h\cdot f_R}{e}\cdot\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\)
Auflösen nach \(n_2\) ergibt gerundet \(n_2=8\).
f) Der Übergang mit der geringsten energetischen Differenz ist der von \(n = 7\) auf \(n = 6\). Die zugehörige Frequenz ist \(f = 9,6 \cdot 10 13\,{\rm Hz}\). Mit \(λ = \frac{c}{f}\) ergibt sich \(λ = 3090\,{\rm nm}\). Der größtmögliche Übergang ist der aus dem Unendlichen auf \(n = 6\). Für \(n_1 \rightarrow \infty\) liefert die Formel \(E = 13,6\,{\rm eV}\). Es ergibt sich \(λ = 819\,{\rm nm}\), beide im Infrarotbereich.
g)
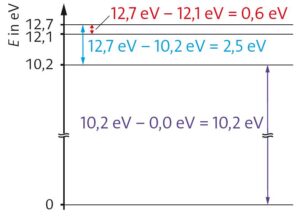
Spektrallinien
Aufgabe 1
Die Farben entstehen durch den Licht emittierenden Teil eines Wolkenkomplexes, aus dem der Orionnebel überwiegend besteht. Dieser enthält einen großen Anteil des Gases Wasserstoff, aber auch 10 % Helium sowie Anteile von Sauerstoff, Kohlenstoff, Neon, Stickstoff, Schwefel und Argon im Staub des Nebels. Durch die hohen Temperaturen von ca. 10000 K werden die Gase zum Leuchten angeregt oder absorbieren weißes Licht.
Aufgabe 2
a) Der Verlauf der Lichtintensitäts-Kurve hat an der mit dem Pfeil gekennzeichneten Stelle einen Einbruch. Das bedeutet, Licht wird abgeschwächt bei einer Wellenlänge von abgelesen \(\lambda = 410\,{\rm nm}\). Die Wellenlänge von \(\lambda = 410,174\,{\rm nm}\) würde zu dem beobachteten Peak passen. Dies entspricht einem Quantenübergang in der Hülle des Wasserstoffatom von \(n_2 = 6\) zu \(n_1 = 2\).
b) Das Hubble-Teleskop kann durch seine Position Strahlung ohne den Einfluss der Atmosphäre untersuchen. Insbesondere bei der Spektralanalyse werden so die gemessenen Wellenlängen nicht durch die verschiedenen Komponenten des Gases beeinflusst. Man vermeidet also die Fraunhoferschen Linien im Spektrum.
Aufgabe 3
a) Es sind Energieübergänge von 0,42 eV; 1,09 eV; 2,11 eV sowie
0,42 eV + 1,09 eV = 1,51 eV;
0,42 eV + 1,09 eV + 2,11 eV = 3,62 eV und
1,09 eV + 2,11 eV = 3,20 eV
möglich. Daraus ergeben sich folgende Wellenlängen: Aus \(E = h \cdot f = h\cdot\frac{c}{\lambda}\) ergibt sich die Wellenlänge zu \(\lambda = h \cdot \frac{c}{E}\). Für den kleinsten Übergang errechnet sich eine Wellenlänge von \(\lambda_1 = 2951,1\,{\rm nm}\). Auf die gleiche Weise errechnen sich die anderen Wellenlängen: \(\lambda_2 = 1137,1\,{\rm nm}\); \(\lambda_3 = 587,43\,{\rm nm}\); \(\lambda_4 =820\,{\rm nm}\); \(\lambda_5 = 342,39\,{\rm nm}\) und \(\lambda_6 = 387,33\,{\rm nm}\). Nur \(\lambda_3\) liegt im sichtbaren Bereich des Spektrums zwischen 400 nm und 800 nm.
b) Individuelle Lösung. Zum Beispiel gibt es im sichtbaren Bereich des Spektrums nur eine charakteristische Spektrallinie des Natriums, anhand derer man das Element eindeutig zuordnen kann. Ebenso sind die Peaks in der Kurve Absorptions-Linien, die sich eindeutig einem Element zuordnen lassen. In diesem Fall Wasserstoff.
Franck-Hertz-Versuch
Aufgabe 1
a) In einer mit Quecksilber-Dampf (Hg) gefüllten Röhre werden Elektronen von der Glühkathode bis zu einer gitterförmigen Zwischenelektrode beschleunigt. Nach dem Gitter gibt es ein Gegenfeld mit Spannung \(U_G\), das die Elektronen am Ende abbremst. Alle Elektronen, welche die Anode erreichen, hatten am Gitter also mindestens die Energie \(e \cdot U_G\) . Durch Messung der Anodenstromstärke \(I_A\) kann untersucht werden, wie sich die an der Anode ankommende Rate der Elektronen verändert.
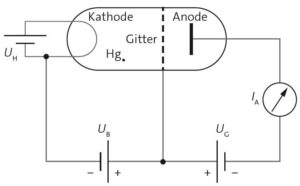
b) Der Anodenstrom fällt beim Erhöhen der Gegenspannung in regelmäßigen Abständen immer wieder ab. Daraus lernt man, dass Atome nur bestimmte Energien aufnehmen können. Die Energieniveaus sind also diskret.
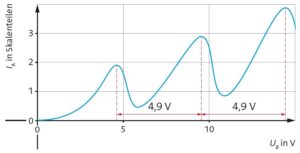
Aufgabe 2
a) Die ablesbaren Peaks liegen bei 16,76 V und 34,15 V und 52,35 V. Die Differenz zwischen zwei Peaks liegt bei 17,4 V bzw. 18,2 V, im Mittel also bei 17,8 V. Die Anregungsernergie läge somit bei \(ΔE = 17,8\,{\rm eV}\) bzw. \(ΔE = 2,252 \cdot 10^{–18}\,{\rm J}\).
b) Mit der Frequenzbedingung ergibt sich \(\lambda=\frac{h\cdot c}{\Delta E}=69,65\,{\rm nm}\).
c) Individuelle Lösung. Die berechnete Wellenlänge liegt im UV-Bereich. Denkbar wäre also ein Sprung auf ein Zwischenniveau, bei dem ein sichtbares Photon ausgesendet wird.
Aufgabe 3
a) Individuelle Lösung. Zum Beispiel erhöht die Temperatur die mittlere Bewegungsgeschwindigkeit der Quecksilberatome und damit die Stoßwahrscheinlichkeit. Damit nimmt der Widerstand der Röhre zu, was einem Sinken der Stromstärke entspricht. Die Lage der Minima/Maxima wird dadurch jedoch nicht beeinflusst.
b) Aus der Grafik entnimmt man z. B. bei 170 °C zwischen dem ersten und zweiten Maximum eine Differenz von \(ΔU_B = 4,7\,{\rm V}\). Das entspricht einer Anregungsenergie von \(ΔE = 4,7\,{\rm eV}\). Aus der Wellenlänge \(λ = 253,6\,{\rm nm}\) der ausgesandten Strahlung erbibt sich mit der Frequenzbedingung \(\Delta E=\frac{h\cdot c}{\lambda}= 4,889\,{\rm eV}\). Der abgelesene Wert ist also etwas geringer (relativer Fehler 3,9 %).
c) Die Geschwindigkeit der Elektronen ergibt sich nach der Formel für die Beschleunigungsspannung: \(v=\sqrt{\frac{2\cdot E_{\rm kin}}{m_e}}=1,968\cdot 10^6\,\frac{\rm m}{\rm s}\)
Eine weitere Geschwindigkeit berechnet sich nach einem inelastischem Stoß mit einem Hg-Atom, wenn das Elektron einen entsprechenden Teil seiner kinetischen Energie abgegeben hat. Es hat dann noch die Energie von \(E_{\rm kin} = 11\,{\rm eV} – 4,9\,{\rm eV} = 6,1\,{\rm eV}\). Analog zur obigen Berechnung ergibt sich dann eine Geschwindigkeit von \(v = 1,466 \cdot 10^6\,\frac{\rm m}{\rm s}\).
Potenzialtopfmodell
Aufgabe 1
a) Einsetzen des Wertes für \(L\) in die Formel für die Energie \(E_n\) im Grundzustand, d. h für \(n = 1\), liefert: \(E_n = 6,0247 \cdot 10^{–18}\,{\rm J} = 37,6\,{\rm eV}\).
b) Um dies zu überprüfen, muss man zeigen, dass die Energiedifferenz \(ΔE\) im Potenzialtopf eines Farbstoffmoleküls der Länge \(L = 1,0 \cdot 10^{−10}\,{\rm m}\) eingesetzt in die Formel \(ΔE = h \cdot f\) bzw. \(ΔE = h \cdot\frac{c}{\lambda}\) eine Wellenlänge im Bereich zwischen 400 nm und 800 nm ergibt. Eingesetzt in die obige Formel ergibt sich \(ΔE = 6,0247 \cdot 10^{–18}\,{\rm J}\cdot (14^2 – 12^2) = 3,133 \cdot 10^{–16}\,{\rm J}\). Diese Energie entspricht einer Wellenlänge von \(\lambda = 6,341 \dot 10^{–10}\,{\rm m} = 63,41\,{\rm nm}\). Sie ist also nicht sichtbar.
Aufgabe 2
a) Durch die Molekülstruktur (konjugierte Doppelbindungen) liegt ein delokalisiertes Elektronensystem vor, in dem sich 8 Elektronen (\(\pi\)-Elektronen oberhalb und unterhalb der Bindungsebene) frei bewegen können. Sie können aber den grau markierten Bereich wegen der Bindungskräfte (Potenzialwall) nicht verlassen. Daher sind die Voraussetzungen für das Modell hier erfüllt.
b) \(L=n\cdot\frac{h}{2\cdot p}=n\cdot\frac{h}{2\cdot m\cdot v}\Rightarrow v=n\cdot\frac{h}{2\cdot m\cdot L}\)
Einsetzen in \(E=E_{\rm kin}=\frac{1}{2}\cdot m\cdot v^2\) liefert:
\(E_n=\frac{1}{2}\cdot m\cdot \frac{h^2\cdot n^2}{4\cdot m^2\cdot L^2}=\frac{h^2\cdot n^2}{8\cdot m\cdot L^2}\)
c)
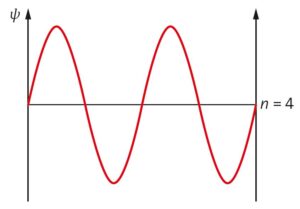
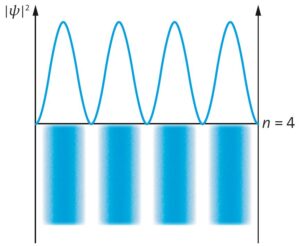
d) Berechnung der Photonenenergie liefert \(E_{\rm Ph} = 3,7 \cdot 10^{−19}\,{\rm J} = 2,312\,{\rm eV}\).
Das höchste besetzte Niveau im Grundzustand ist das für \(n =4\). Einsetzen in die Formel für die Energie \(E_4 = \frac{h^2 \cdot n^2}{8\cdot m\cdot L^2}\) ergibt mit \(L = 1,21\,{\rm nm}\) die Energie \(E_4 = 4,11\,{\rm eV}\). Die Energieniveaus liegen bei \(E_7 = 12,58\,{\rm eV},\ E_6 = 9,25\,{\rm eV},\) \(E_5 = 6,42\,{\rm eV},\) \(E_3 = 2,31\,{\rm eV},\) \( E_2 = 1,02\,{\rm eV}\ \text{und}\ E_1 = 0,26\,{\rm eV}\).
Direkt nach der Absorption befände sich das Elektron in \(E_5\) mit \(ΔE = E_5 – E_4 = 2,31\,{\rm eV}\).
Fluoreszenz
Aufgabe 1
a) Mit der Einsteinschen Frequenzbedingung lässt sich die Wellenlänge einem Energieübergang im Molekül zuordnen. Mit \(λ = 198,2\,{\rm nm}\) eingesetzt in \(ΔE = h \cdot \frac{c}{\lambda}\) ergibt sich \(ΔE = 6,25\,{\rm eV}\), wobei \(h = 4,1357 \cdot 10^{–15}\,{\rm eVs}\) eingesetzt werden muss. Dies ist möglich durch einen Übergang vom 5. zum 3. Energieniveau \((ΔE = 3,52\,{\rm eV} + 2,74\,{\rm eV})\).
b) Ein denkbarer Übergang von Niveau 5 auf Niveau 4 als Zwischenniveau könnte einen verzögerten Übergang vom 4. auf das 3. Niveau zur Folge haben. Dabei würde nach obiger Rechnung ein Photon mit der Wellenlänge \(λ = 452,36\,{\rm nm}\) abgestrahlt. Es wäre sichtbar.
Aufgabe 2
a) Individuelle Lösung Das obere Sprektrum bildet z. B. den sichtbaren Anteil der UV-LED ohne Filter ab. Das untere Spektrum besteht aus drei unterschiedlichen Farben, deren Wellenlängen offensichtlich größer sind als die, die die UV-Diode aussendet. Das ist nur zu erklären, wenn man annimmt, dass es im Material der grünen Platte zu Fluoreszenzerscheinungen kommt.
b) Messergebnisse zu den beobachteten Sprektrallinien (Abstand zwischen dem rechten und linken Maximum erster Ordnung geteilt durch 2):
Oben (violett): \(a_1 = 4,75/2\,{\rm cm} = 2,375\,{\rm cm}\)
Unten (gelbgrün): \(a_1 = 6,20/2\,{\rm cm} = 3,10\,{\rm cm}\)
(grün): \(a_1 = 6,00/2\,{\rm cm} = 3,00\,{\rm cm}\)
(blaugrün): \(a_1 = 5,80/2\,{\rm cm} = 2,90\,{\rm cm}\)
Mit der Formel zur Berechnung der Wellenlängen von Spektrallinien bei gegebener Gitterkonstante von \(g = \frac{500}{\rm mm} = 2,0 \cdot 10^{–6}\,{\rm m}\) und dem Schirmabstand von \(e = 11,3\,{\rm cm}\) folgt für violett:
\(\lambda=g\cdot \sin\left[\tan^{-1}\left(\frac{a}{e}\right)\right]=4,1137\cdot 10^{-7}\,{\rm m}=411,37\,{\rm nm}\),
gelbgrün: \(\lambda = 529,12\,{\rm nm}\),
grün: \(\lambda = 513,20\,{\rm nm}\),
blaugrün: \(\lambda = 497,16\,{\rm nm}\).
Mit \(ΔE = h \cdot \frac{c}{\lambda}\) erhält man die folgenden Photonenenergien:
Violett: \(ΔE_v = 3,013\,{\rm eV}\),
gelbgrün: \(ΔE_{gg} = 2,3425\,{\rm eV}\),
grün: \(ΔE_g = 2,4152\,{\rm eV}\),
blaugrün: \(ΔE_{bg} = 2,4931\,{\rm eV}\).
Da es sich bei der Fluoreszenzplatte um einen Festkörper handelt, ist ein mögliches Energieniveauschema nicht einfach mit dem eines Einzelatoms vergleichbar und erklärbar. Es lässt sich aber ein Schema mit den entsprechenden Abständen skizzieren, wenn man die berechneten Photonenenergien als Elektronenübergänge betrachtet.
\(ΔE_{\rm violett} = 3,013\,{\rm eV}\) wird vom Filter vollständig absorbiert. Von dem oberen Niveau wechseln die Elektronen auf die Zwischenniveaus, von denen sie anschließend auf das Ausgangsniveau zurückfallen.

Laser
Aufgabe 1
Ein Laser beruht auf dem Prinzip der stimulierten Emission. Wenn Photonen passender Wellenlänge auf ein Atom, z. B. in einem Gas, im angeregten Zustand treffen, können sie Elektronen dazu stimulieren, auf ein niedrigeres Energieniveau überzugehen. Das dabei emittierte Photon hat die gleiche Wellenlänge wie das stimulierende. So wird die eintreffende Strahlung verstärkt.
In Abb. 7 wird beim Übergang vom oberen zum unteren Laserniveau ein Photon ausgesendet. Die zur Verfügung gestellten und entstandenen Photonen für die stimulierte Emission können in einem Resonator (z. B. Spiegel) gehalten werden, sodass sie weitere Übergänge anregen. kann Durch die stimulierte Emission entsteht so eine große Anzahl von Photonen der gleichen Energie, die dann gebündelt in einem Laserstrahl über ein Spiegelsystem extrahiert werden können.
Aufgabe 2
a) Der angeregte Zustand beim Stickstoffmolekül liegt \(0,3\,{\rm eV} = 4,81 \cdot 10^{–20}\,{\rm J}\) über dem Grundzustand. Mit der Formel für die kinetische Energie für thermische Elektronen \(E =\frac{1}{2}\cdot m_e\cdot v^2\) erhält man eine Geschwindigkeit von \(v = 325000\,\frac{\rm m}{\rm s}\).
b) Die Bewegungsenergie (thermische Energie) der \(\text{N}_2\)-Moleküle muss mindestens den Betrag von \(E_\,{\rm kin} = 2,2 \cdot 10^{−3}\,{\rm eV}\) erreichen.
© Cornelsen Verlag GmbH, Berlin