Welleneigenschaften
Aufgabe 1
a) Als Beispiel eignet sich eine Seilwelle auf dem Boden. Sie wird horizontal ausgeschlagen. Eine farblich markierte Stelle des Seils (Oszillator) bewegt sich nicht in Wellenrichtung. Ein Kreidestück neben dem Seilende wird durch den ankommenden Wellenberg weggeschubst. Durch die konstante Position der Markierung wird deutlich, dass sich die Oszillatoren der Welle nicht bewegen, also keine Materie transportiert wird. Die Energieübertragung zeigt, dass die Welle durch ihre Bewegung Energie transportiert.
b) Es genügt, einen Polarisationsfilter als Analysator in den Strahlengang eines Laserstrahls zu halten und diesen zu drehen, bis kein Licht durch den Filter gelassen wird. Beim Licht einer Glühlampe werden zwei Polarisationsfilter benötigt, die gekreuzt in den Strahlengang gehalten werden. Während Laserlicht bereits polarisiert ist, wird weißes Licht erst durch den ersten Filter polarisiert, so dass die Welle nur in einer Ebene schwingt. Der zweite Polarisationsfilter dient dann als Analysator.
c) Die Moleküle (nahe) der Wasseroberfläche bewegen sich auf Kreisbahnen entgegen der Ausbreitungsrichtung der Welle und um einen fixen Punkt. Durch die zeitliche Verzögerung zwischen den Bewegungen benachbarter Moleküle ergibt sich insgesamt eine Welle, die sich senkrecht zur Ausbreitungsrichtung hebt und senkt.
Aufgabe 2
a) Wir berechnen: \(T=\frac{1}{f}=\frac{1}{\rm 3\,Hz}=\frac{1}{\rm 3\,s}\)
\(c=\frac{x}{t}=\frac{\rm 24\,cm}{\rm 1\,s}=0,24\,\frac{\rm m}{\rm s}\)
\(\lambda=c\cdot f=8\,{\rm cm}\Rightarrow s(t,c)=4\,{\rm cm}\cdot \sin\left(2\pi\cdot\left(\frac{3}{\rm s}\cdot t-\frac{x}{\rm 8\,cm}\right)\right)\)
b) Eine mögliche Lösung ist die folgende:
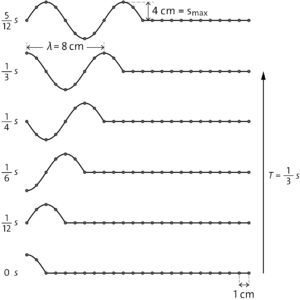
Aufgabe 3
a) Wir formulieren die Gleichung für \(t+T\) aus:
\(s(t+T,x)=s_{\rm max}\cdot\sin\left(2\pi\cdot \left(\frac{t+T}{T}-\frac{x}{\lambda}\right)\right)\)
\(=s_{\rm max}\cdot\sin\left(2\pi\cdot \left(\frac{T}{T}+1-\frac{x}{\lambda}\right)\right)\)
\(=s_{\rm max}\cdot\sin\left(2\pi\cdot \left(\frac{t}{T}-\frac{x}{\lambda}\right)+2\pi\right)\)
\(=s_{\rm max}\cdot\sin\left(2\pi\cdot \left(\frac{t}{T}-\frac{x}{\lambda}\right)\right)=s(t,x)\)
b) Wir formulieren die Geleichung für \(x+\lambda}) aus:
\(s(t,x+\lambda)=s_{\rm max}\cdot\sin\left(2\pi\cdot \left(\frac{t}{T}-\frac{x+\lambda}{\lambda}\right)\right)\)
\(=s_{\rm max}\cdot\sin\left(2\pi\cdot \left(\frac{t}{T}-\frac{x}{\lambda}-1\right)\right)\)
\(=s_{\rm max}\cdot\sin\left(2\pi\cdot \left(\frac{t}{T}-\frac{x}{\lambda}\right)-2\pi\right)\)
\(=s_{\rm max}\cdot\sin\left(2\pi\cdot \left(\frac{t}{T}-\frac{x}{\lambda}\right)\right)=s(t,x)\)
Aufgabe 4
a) Für \(x = 0\,{\rm m}\) ergibt sich aus der Wellenfunktion die Bewegungsgleichung des Senders: \(𝑠(0\,{\rm m}, 𝑡) = −0,32\,{\rm m}\cdot \sin\left(\pi\cdot\frac{t}{2\,{\rm s}}\right)\)
Die Amplitude beträgt also 32 cm und zum Zeitpunkt \(t = 0\,{\rm s}\) beginnt der Sender in der Gleichgewichtslage mit einer Bewegung nach unten, da es sich um eine negative Sinusfunktion handelt.
b) Um \(T\) und \(\lambda\) zu bestimmen, muss man das Argument der Sinusfunktion in die Form \(2𝜋\cdot\left(\frac{t}{T}\pm\frac{x}{\lambda}\right)\) bringen:
\(\pi\cdot \left(\frac{t}{\rm 2\,s}\pm\frac{2,5x}{\rm m}\right)=2\pi\cdot \left(\frac{t}{\rm 4\,s}\pm\frac{x}{\rm 0,8\,m}\right)\)
Daraus ergibt sich \(4,0\,{\rm s}\ \text{und}\ \lambda=0,8\,{\rm m}\).
c) Die Welle bewegt sich nach links: Im Argument der Sinusfunktion wird der Term \(\frac{x}{\rm 0,8\,m}\), die Phasendifferenz zwischen dem Sender und der Stelle \(x\), an dem der Wellenträger schwingt, addiert, sodass bei negativem (positivem) \(x\) auch diese Phasendifferenz negativ (positiv) ist, d. h., dass das Signal an dieser Stelle später (früher) gemessen wird.
d)Wir berechnen:
\(s(1,5\,{\rm m},\ 8,0\,{\rm s})=-0,32\,{\rm m}\cdot\sin\left(\pi\cdot \left(\frac{\rm 8\,s}{\rm 2\,s}-\frac{\rm 2,5\cdot 1,5\,m}{\rm m}\right)\right)\)
\(=-0,32\,{\rm m}\cdot\sin(7,75\pi)=-0,32\,{\rm m}\cdot\sin(1,75\pi)=-0,32\,{\rm m}\cdot\left(-\frac{\sqrt{2}}{2}\approx 0,23\,{\rm m}\right)\)
Ausbreitung von Wellen
Aufgabe 1
a) Amplitude: \(s_{\rm max}=4\,{\rm cm}\); Periodendauer: \(T=2\,{\rm s}\); Frequenz: \(f=\frac{1}{T}=0,5\,{\rm Hz}\); Wellenlänge: \(\lambda=c\cdot T=2\,\frac{\rm m}{\rm s}\cdot 2\,{\rm s}=4\,{\rm m}\)
b) \(s(t,x)=5\,{\rm cm}\cdot\sin\left(2\pi\cdot \left(\frac{t}{\rm 2\,s}-\frac{x}{\rm 4\,m}\right)\right)\)
c) Auslenkung für einen festen Ort \(x=0\):
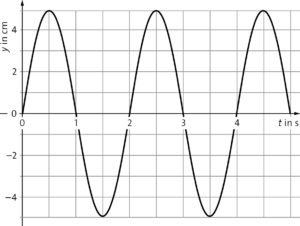
Auslenkung für einen festen Zeitpunkt \(t=0\):
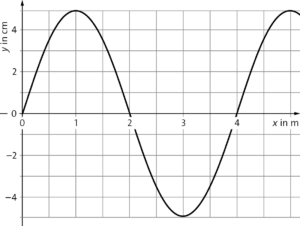
Aufgabe 2
Der Abbildung ist zu entnehmen, dass die Wellenlänge 0,5 cm beträgt. Zusammen mit der Frequenz von 50 Hz ergibt sich die Ausbreitungsgeschwindigkeit zu: \(c=\lambda\cdot f=5\,{\rm mm}\cdot 50\,{\rm Hz}=0,25\,\frac{\rm m}{\rm s}\)
Aufgabe 3
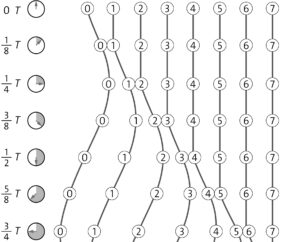
a) In Spalten sind die Zustände derselben Oszillatoren zu unterschiedlichen Zeitpunkten dargestellt. In Zeilen sind dann die Zustände aller betrachteten Oszillatoren zu einem bestimmten Zeitpunkt zu sehen. Durch die Momentaufnahmen ist von oben nach unten die seitliche Ausbreitung einer Welle über die Oszillatoren zu sehen, die anfangs in Ruhe waren. Bezogen auf einen einzelnen Oszillator ist dessen Schwingung zu erkennen.
b) In diesem Fall müssen alle Abbildungen für die einzelnen Zeitpunkte an der Waagerechten durch die Ruhelagen nach unten gespiegelt werden. Außerdem liegt der Beginn \(\frac{1}{4} 𝑇\) später.
c)
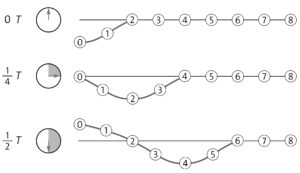
d) Während einer Periodendauer vollführt ein Oszillator eine vollständige Schwingung. Seine Geschwindigkeit ändert sich dabei ständig (maximal beim Durchgang durch die Ruhelage, minimal an den Umkehrpunkten). In der gleichen Zeit schreitet die Welle um eine Wellenlänge voran. Dies erfolgt mit der konstanten Ausbreitungsgeschwindigkeit der Welle.
e)
Überlagerung von Wellen
Aufgabe 1
Aufgabe 2
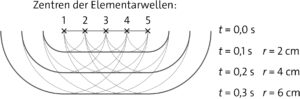
Aus der Abbildung lassen sich folgende Streckenlängen ablesen:
\(\overline{E_1P}=2,5\lambda\)
\(\overline{E_2P}=2\lambda\)
Damit ergibt sich der Gangunterschied: \(\Delta s=\overline{E_1P}-\overline{E_2P}=0,5\lambda\). Das entspricht destruktiver Interferenz, die Wellen löschen sich also an dieser Stelle aus.
Aufgabe 3
a) Rücken die Erreger weiter auseinander, dann werden die Hyperbeln mit den Bereichen konstruktiver und destruktiver Interferenz zahlreicher und liegen entsprechend dichter.
b) Gleiches ergibt sich, wenn beide Erreger schneller schwingen.
c) Schwingen die beiden Erreger gegenphasig, dann tauschen die Bereiche konstruktiver und destruktiver Interferenz.
Aufgabe 4
a) Bei der Reflexion der Welle an den Pits entstehen nach dem Huygensschen Prinzip Elementarwellen an den Pits. Je nach Abstand kommt es zu konstruktiver bzw. destruktiver Interferenz des Laserlichts auf dem Schirm. Die Spurweite entspricht dem Spaltabstand bzw. der invertierten Gitterkonstante bei einem Gitter.
b) Gegeben: \(a=0,42\,{\rm m}\) und \(d_1=37,3\,{\rm cm}-22,4\,{\rm cm}=14,9\,{\rm cm}\)
Damit lässt sich die Gitterkonstante berechnen: \(g=\frac{n\cdot \lambda}{\sin\left(\arctan\left(\frac{d_n}{a}\right)\right)}=\frac{\lambda}{\sin\left(\arctan\left(\frac{d_1}{a}\right)\right)}\approx1,59\,{\rm µm}\)
c) Wenn der Laser mit der kleineren Wellenlänge genutzt wird, dann werden die Beugungswinkel kleiner und die Maxima des Interferenzbildes rücken näher aneinander.
d) Entsprechend der Antwort zu c) ist der Laser eines Blu-Ray-Players geeignet, eine CD abzuspielen, da die Beugungseffekte verringert werden. Die kleinere Gitterkonstante einer Blu-Ray-Disc würde bei Verwendung in einem CD-Player dagegen dazu führen, dass die Beugungseffekte größer wären als bei Verwendung einer CD. Konkrete Daten dazu (real genutzte Wellenlängen):
| \(\lambda\) in nm | Spurweite | minimale Pitgröße | |
| CD-ROM | 780 | 1600 nm | 830 nm |
| Blu-Ray-Disc | 405 | 320 nm | 150 nm |
Stehende Wellen
Aufgabe 1
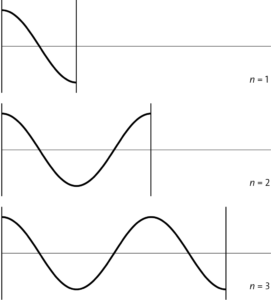
Wie bei einer stehenden Welle mit zwei festen Enden ergibt sich hier eine stehende Welle, wenn für die Länge \(𝑙\) der Flöte gilt: \(𝑙 = 𝑛 \cdot \frac{\lambda_n}{2}\) mit \(𝑛 = 1,\ 2,\ 3\ …\)
Aufgabe 2
a) Wenn die Saite durch die Kraft im Magnetfeld ausgelenkt wird, wandert ein entsprechender Wellenberg entlang der Saite, die als Wellenträger der Länge \(l\) dient. Bei der Reflexion an einem Ende wird aus dem Wellenberg ein Wellental und am anderen Ende aus diesem wieder ein Wellenberg, der nach \(2l\) wieder beim Magnetfeld ankommt. Ist dieser Gangunterschied ein ganzzahliges Vielfaches der Wellenlänge, kommt es zur konstruktiven Interferenz. Das geschieht daher nur bei bestimmten Eigenfrequenzen. In diesem Fall bildet sich auf der Saite eine stehende Welle aus, da durch die mehrfache Reflexion sich gegenläufige Wellen überlagern.
b)
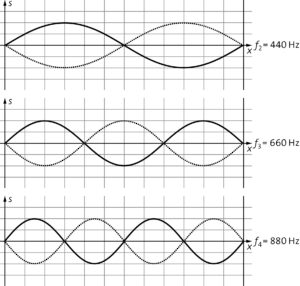
c) Wenn der Magnet im Bereich eines Knotens steht, kann er keine stehende Welle anregen. Steht er z. B. bei 440 Hz in der Mitte von P und Q, sollte sich die Saite dort gar nicht bewegen. Im Bereich des Magnetfelds direkt rechts und links von der Mitte müsste auf einen Teil der Saite eine Kraft nach oben und auf den anderen eine nach unten ausgeübt werden, da sie sich gegenphasig bewegen sollen. Das ist bei gleicher Stromrichtung und Feldlinienrichtung unmöglich. Der Magnet muss daher vom Knoten weg verschoben werden.
d) An festen Enden sind einlaufende und reflektierte Welle immer gegenphasig und überlagern sich deswegen als gegenläufige Wellen dort zu einem Knoten einer stehenden Welle. Der Abstand zwischen zwei benachbarten Knoten beträgt \(\frac{\lambda_k}{2}\), d. h., der Abstand zwischen den Knoten an den beiden Enden muss ein Vielfaches davon betragen, d. h. \(l=k\cdot\frac{\lambda_k}{2}\).
Aufgabe 3
a) Mit \(c=\lambda\cdot f=2\cdot\overline{PQ}\cdot f\) ergeben sich die folgenden Werte:
| \(m\) in kg | 0,50 | 1,25 | 2,75 | 3,50 | 4,00 |
| \(\overline{PQ}\) in cm | 25 | 40 | 60 | 67 | 72 |
| \(c\) in \(\frac{\rm m}{\rm s}\) | 110 | 176 | 264 | 295 | 317 |
| \(F\) in N | 4,9 | 12,3 | 27,0 | 34,3 | 39,2 |
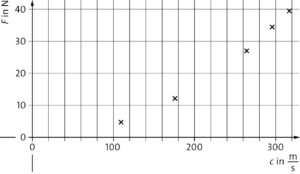
b) Das Diagramm zeigt, dass die Ausbreitungsgeschwindigkeit der Welle auf der Saite mit der Spannkraft zunimmt. Je größer die Ausbreitungsgeschwindigkeit ist, desto stärker ist die Kopplung zwischen den Teilen eines Wellenträgers, hier also der Saite. Daher gilt: Je größer die Spannkraft ist, desto stärker ist die Kopplung.
c) Die Werte im \(F\)-\(c\)-Diagramm liegen nicht auf einer Ursprungsgeraden, das heißt sie sind nicht proportional zueinander. Am \(F\)-\(c^2\)-Diagramm zeigt sich die Proportionalität deutlich:
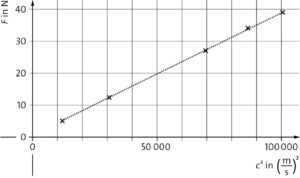
Es gilt \(k=\frac{c^2}{F}\), d. h., \(k\) ist der Kehrwert der Steigung der Ausgleichsgeraden im \(F\)-\(c^2\)-Diagramm. Hier ergibt sich ein Wert von \(2560\,\frac{\rm m}{\rm kg}\).
Alternative: \(\frac{c^2}{F}\) für jede Messung berechnen und den Mittelwert bilden.
Reflexion und Brechung
Aufgabe 1
a) Wenn die Wellen senkrecht auf die Wand treffen, bildet sich durch die Überlagerung von einfallender und reflektierter Welle eine stehende Welle aus. Aufgrund des Phasensprungs besitzt diese an der Wand einen Knoten. Die Knoten, also die Punkte ohne Empfang, befinden sich im Abstand einer halben Wellenlänge voneinander, also im Abstand von
\(n\cdot \frac{\lambda}{2}=n\cdot \frac{c}{2f}\approx n\cdot 0,083\,{\rm m}\)
von der Wand (\(n = 0,\ 1,\ 2,\ …\)). Der Empfang ist in der Mitte der Bäuche am besten, also jeweils um \(\frac{\lambda}{4}\) dazu versetzt. Somit beträgt der Abstand von der Wand
\(n\cdot \frac{\lambda}{2}+\frac{\lambda}{4}=\left(n+\frac{1}{2}\right)\cdot\frac{c}{2f}\approx\cdot 0,083\,{\rm m}+0,042\,{\rm m}\).
b) Es gilt \(0,5\,{\rm m} = 6 \cdot 0,083\,{\rm m} = 6 \cdot\frac{\lambda}{2}\) . In diesem Abstand hat man demnach keinen Empfang.
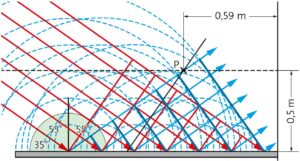
c) Lösung anhand des Huygensschen Prinzips: Betrachtet man die Punkte, in denen Strahlen auf die Wand treffen, als Ausgangspunkte von Elementarwellen, lässt sich die reflektierte Welle wie in der Abbildung rechts konstruieren. Einfalls- und Reflexionswinkel sind gleich groß.
d) Die einfallende Welle legt von der ersten eingezeichneten Wellenfront zu Punkt P eine Strecke von \(1,8\lambda\) zurück, die reflektierte Welle jedoch \(5,2\lambda\): \(d = 5,2 λ − 1,8 λ = 3,4 λ\).
Die Bedingung für destruktive Interferenz ist fast erfüllt, der Empfang in Punkt P ist sehr schlecht.
e) Zur Verbesserung des Empfangs sollte in Punkt P ein Interferenzmaximum vorliegen. Dazu könnte man Punkt P etwas höher setzen oder eine Metallplatte schräg vor die Wand stellen, um den Reflexionswinkel zu verbessern.
Aufgabe 2
a) Die Zeichnung führt zu einem Brechungswinkel von etwa 40°:

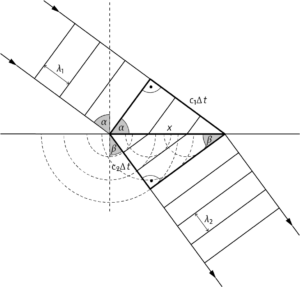
b) An der Grenzfläche zwischen den beiden Medien ergeben sich zwei rechtwinklige Dreiecke (s. u.). Für diese gilt:
\(\sin(\alpha)=\frac{c_1\cdot\Delta t}{x}\) und \(\sin(\beta)=\frac{c_2\cdot\Delta t}{x}\) und damit: \(\frac{c_1\cdot\Delta t}{x}=x=\frac{c_2\cdot\Delta t}{x}\Leftrightarrow \frac{c_1\cdot\Delta t}{c_2\cdot\Delta t}=\frac{c_1}{c_2}=\frac{\sin(\alpha)}{\sin(\beta)}\)
c) \(\alpha =53°\); \(\beta =36°\); \(c_1 =30\,\frac{\rm cm}{\rm s}\Rightarrow c_2=c_1\cdot=\frac{\sin(\beta)}{\sin(\alpha)}\approx 22\,\frac{\rm cm}{\rm s}\)
\(\alpha =65°\); \(c_1 =35\,\frac{\rm cm}{\rm s}; c_2=25\,\frac{\rm cm}{\rm s}\Rightarrow \beta=\arcsin\left(\frac{c_2}{c_1}\cdot\sin(\alpha)\right)\approx40°\)
Die Berechnungen passen zu den vorherigen Ergebnissen.
Interferenzexperimente
Aufgabe 1
a) Doppelspalt:
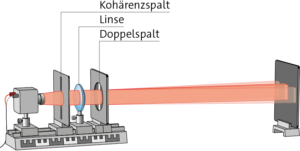

Wenn kohärentes, also überlagerungsfähiges, Licht auf einen schmalen Doppelspalt trifft, entstehen zwei Elementarwellen. Diese überlagern sich hinter dem Spalt. Dort, wo sie aufeinander treffen, entscheidet ihre Interferenzbedingung darüber, ob es zu einer Verstärkung oder Auslöschung kommt. Beträgt der Gangunterschied \( \Delta s=n\cdot\lambda\) mit \(n=1,\ 2,\ 3,\dots\) , also ein ganzzahliges Vielfaches einer Wellenlänge, überlagern die beiden Wellen konstruktiv. Die Bedingung hängt von Spaltabstand und Wellenlänge ab. Die Wellenberge und -täler verstärken sich bei konstruktiver Interferenz. Auf einem entfernten Schirm kommt es dann zu einem Maximum im Interferenzbild.
Sind die Wellen um ein Vielfaches einer halben Wellenlänge gegeneinander versetzt, kommt es zur Auslöschung und auf dem Schirm sieht man nichts. Da konstruktive und destruktive Interferenz vom Ort abhängen, ergibt sich auf dem Schirm ein Interferenzmuster mit abwechselnden Stellen geringer und hoher Interferenz. Die Maxima und Minima werden von der Mitte des Schirms (Verlängerung des Lots auf die Spaltmitte) gezählt und heißten \(n\)-ter (also 1., 2., 3. usw.) Ordnung. Durch Messung dieser Abstände \(d_n\) kann man bei bekanntem Spaltabstand \(g\) und Abstand \(a\) zum Schirm die Wellenlänge des verwendeten Lichts bestimmen.
b) Entsprechend der Beschreibung in a) setzen wir den Winkel \(\alpha\) über die geometrischen Größen gleich:
Durch Winkelbetrachtung sieht man \(\tan(\alpha)=\frac{d_n}{a}\) und \(\sin(\alpha)=\frac{\Delta s}{g}\). Wenn der Schirm im Vergleich zum Spaltabstand sehr weit entfernt ist, kann man die Kleinwinkelnäherung \(\tan(\alpha)\approx \sin(\alpha)\) annehmen und gleichsetzen: \(\frac{d_n}{a}=\frac{\Delta s}{g}\)
Für konstruktive Interferenz ist \(\Delta s=n\cdot \lambda\) und es ergibt sich eine Formel für die Orte der Maxima: \(d_n=\frac{a\cdot \lambda}{g}\cdot n\) mit \(n=1,\ 2,\ 3,\dots\)
Aufgabe 2
a) Wenn der Schirmabstand vergrößert wird, dann wird das Schirmbild gestreckt.
b) Wird der Spaltabstand verkleinert, dann wird das Schirmbild ebenfalls gestreckt.
c) Wird die Wellenlänge vergrößert, so wird das Schirmbild wieder gestreckt.
Aufgabe 3
a)
| \(n\) | \(\alpha_{n,\text{vio}}\) | \(\alpha_{n,\text{rot}}\) | \(d_{n,\text{vio}}\) | \(d_{n,\text{rot}}\) |
| 1 | 11,5° | 23,0° | 0,41 m | 0,85 m |
| 2 | 23,6° | 51,3° | 0,87 m | 2,49 m |
| 3 | 36,9° | – | 1,50 m | – |
| 4 | 53,1° | – | 2,67 m | – |
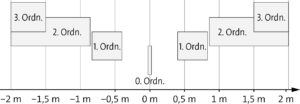
b) Das erste Spektrum beginnt bei 0,41 m und endet bei 0,85 m. Das zweite Spektrum erstreckt sich von 0,87 m bis 2,49 m, es überlappt nicht mit dem ersten Spektrum. Das dritte Spektrum beginnt bei 1,50 m und überlappt daher mit dem zweiten Spektrum. Das vierte Spektrum beginnt bei 2,47 m und ist damit auf dem insgesamt 4,0 m breiten symmetrisch angebrachten Schirm nicht zu beobachten.
Aufgabe 4
a) Für die Winkel und die Lagen der Minima gelten folgende Gleichungen:
\(\sin(\beta_l)=\frac{l\cdot \lambda}{b}\) mit \(l=1,\ 2,\ 3,\dots\) und \(\tan(\beta_l)=\frac{d_l}{a}\)
Für kleine Winkel ist \(\sin(𝛽_𝑙 ) = \tan(𝛽_𝑙)\) und es gilt: \(\frac{l\cdot \lambda}{b}=\frac{d_l}{a}\) mit \(l=1,\ 2,\ 3,\dots\)
Umgestellt nach \(𝑑_𝑙\) liefert: \(d_l=l\cdot\frac{\lambda\cdot a}{b}=l\cdot C\) mit \(C=1,\ 2,\ 3,\dots\)
Man erkennt, dass die Positionen 𝑑𝑙 proportional zu \(𝑙\) sind, allerdings nur für \(l=1,\ 2,\ 3,\dots\) Für 𝑙 = 0 erhält man kein Minimum, sondern das Hauptmaximum.
b) In der Mitte befindet sich ein heller und breiter Fleck (mit dem sogenannten Hauptmaximum). Links und rechts davon beobachtet man deutlich schwächere und schmalere Flecken (mit den sogenannten Nebenmaxima). Die Intensität der Nebenmaxima nimmt mit zunehmender Ordnung schnell ab. Das Hauptmaximum und die Minima sind im Rahmen der Kleinwinkelnäherung äquidistant verteilt.
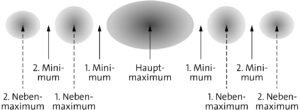
c) Bei einer Verdopplung der Spaltbreite wird das Schirmbild gestaucht (mit einem Faktor 0,5). Gleichzeitig nimmt die Intensität stark zu, da einerseits durch einen Spalt mit doppelter Breite doppelt so viel Licht gelangt und andererseits das Licht in den schmaleren Maxima stärker konzentriert wird.
Doppelspalt und Gitter
Aufgabe 1
Das Schirmbild zeigt abwechselnd helle und dunkle Streifen. Die hellen Streifen sind die Intensitätsmaxima, die dunklen die Intensitätsminima. Die Abstände benachbarter Maxima sind gleich groß. Das Maximum 0. Ordnung ist am hellsten, die Helligkeit nimmt bis zum 4. Maximum ab. Das Maximum 5. Ordnung fehlt, die Maxima der 6. bis 9. Ordnung haben eine sehr geringe Helligkeit.
Das Licht wird an jedem der Spalte gebeugt. Für bestimmte Richtungen interferieren die Lichtwellen destruktiv. An den entsprechenden Stellen ist die Intensität auf dem Schirm null, auch wenn dort ein Doppelspalt-Maximum zu erwarten wäre. Das fehlende Doppelspalt-Maximum fällt in ein Einzelspalt-Minimum.
Aufgabe 2
Da die Maxima der 5. Ordnung fehlen, muss der Winkel \(\alpha_5\) für das 5. Doppelspalt-Maximum mit dem Winkel \(β_1\) für das 1. Einzelspalt-Minimum zusammenfallen. Aus \(\sin(\alpha_5) = \sin(\beta_1)\) folgt \(g = 5b = 5,0 \cdot 10^{−4}\,{\rm m}\). Entsprechend fällt das 10. Doppelspalt-Maximum in das 2. Einzelspalt-Minimum.
Mit der Kleinwinkelnäherung kann man den Abstand benachbarter Intensitätsmaxima berechnen: \(\Delta d=\frac{\lambda\cdot a}{g}=1,1\,{\rm mm}\)
Aufgabe 3
Die Gitterkonstante beträgt \(g=\frac{\rm 1\cdot 10^{-3}\,m}{200}=5,0\cdot 10^{-6}\,{\rm m}\). Für den Winkel \(\alpha_{\rm max}\) zu den Rändern des Schirms gilt: \(\tan(\alpha_{\rm max})=\frac{d}{a}=\frac{\rm 0,50\,m}{\rm 1,00\,m}\Rightarrow \alpha_{\rm max}=26,6°\)
Für die Winkel \(\alpha_{n}\) der auf dem Schirm beobachtbaren Maxima muss gelten: \(\alpha_n<\alpha_{\rm max}\Rightarrow\sin(\alpha_n)=\frac{n\cdot \lambda}{g}<\sin(\alpha_{\rm max})\)
Daraus folgt für die Ordnung der Maxima auf dem Schirm: \(n<g\cdot\frac{\sin(\alpha_{\rm max})}{\lambda}=4,2\)
Es sind also nur Maxima bis zur 4. Ordnung beobachtbar. Mit dem Maximum 0. Ordnung sind damit neun Intensitätsmaxima auf dem Schirm zu sehen.
Aufgabe 4
Weißes Licht enthält Licht unterschiedlicher Wellenlängen. Je größer die Wellenlänge ist, desto größer ist der Winkel, bei dem es zur konstruktiven Interferenz kommt. Das bedeutet, dass violettes Licht mit der kleinsten Wellenlänge am weitesten innen im Spektrum zu beobachten ist. Daran schließen sich blaues, grünes, gelbes und rotes Licht an.
Man vergleicht den Winkel für das Maximum von rotem Licht in zweiter Ordnung mit dem für violettes Licht in 3. Ordnung:
\(\sin(\alpha_{2,\text{rot}})=\frac{2\cdot\lambda_{\rm rot}}{g}=\frac{\rm 2\cdot 780\cdot 10^{-9}\,m}{\rm 5\cdot 10^{-6}\,m}=0,31\Rightarrow \alpha_{2,\text{rot}}=18°\)
\(\sin(\alpha_{3,\text{vio}})=\frac{3\cdot\lambda_{\rm vio}}{g}=\frac{\rm 3\cdot 400\cdot 10^{-9}\,m}{\rm 5\cdot 10^{-6}\,m}=0,24\Rightarrow \alpha_{2,\text{vio}}=14°\)
Da \(\alpha_{2,\text{rot}}>\alpha_{3,\text{vio}}\) ist, überlappen die Spektren. Nun berechnet man die Wellenlänge des Spektrums 2. Ordnung beim Winkel \(\alpha_{3,\text{vio}}\):
\(\lambda=\frac{g\cdot\sin(\alpha_{3,\text{vio}})}{2}=\frac{\rm 5\cdot 10^{-6}\,m\cdot\sin(14°)}{2}=600\,{\rm nm}\)
Das Spektrum 2. Ordnung ist also von 400 nm bis etwa 600 nm nicht überlagert.
Michelson-Interferometer
Aufgabe 1
In Luft ist die Wellenlänge geringfügig kleiner als im Vakuum. In der evakuierten Kammer hat das Licht die sogenannte Vakuumwellenlänge. Lässt man langsam Luft in die Kammer, dann verkleinert sich die Wellenlänge. Passt in die Länge der Kammer zusätzlich ein Viertel der Wellenlänge, dann bedeutet dies eine Phasenverschiebung von \(\frac{1}{2}\pi\). Da das Licht die Kammer einmal vor und einmal nach der Reflexion am Spiegel 1 durchläuft, wird die Phase des hin und her laufenden Lichts um 𝜋 verschoben. Auf das vom Spiegel 2 kommende Licht wirkt sich dies nicht aus. Wenn also zu Beginn das Licht aus den beiden Strahlengängen an einer Stelle des Schirms konstruktiv interferiert, dann interferiert es dort nun destruktiv und umgekehrt. Folglich wechseln helle Stellen zu dunklen und umgekehrt.
Aufgabe 2
Wenn man in der Schirmmitte 76 Wechsel von hell zu dunkel zählt, dann hat sich die Phase des Lichts auf dem Strahlengang 1 um \(76 \cdot 2𝜋\) verschoben. (Bei 76 Wechseln von hell zu dunkel sind auch 76 Wechsel von dunkel zu hell dazwischen.) Dies entspricht 76 Wellenlängen. Bezogen auf einen Kammerdurchgang sind dies 38 Wellenlängen. In Luft passen also 38 Wellenlängen mehr auf die Länge \(l\) der Kammer als im Vakuum. Wenn \(k\) die Anzahl der Wellenlängen in der evakuierten Kammer ist, dann gilt also: \(l = k \cdot 𝜆_0 = (n + 38) \cdot \lambda_L\)
Für die Brechzahl von Luft gilt: \(n_L=\frac{\lambda_0}{\lambda_L}=\frac{k+38}{k}=1+\frac{38}{k}=1+\frac{38\cdot\lambda}{l}\)
Mit der angegebenen Wellenlänge von 633 nm des Laserlichts folgt die Brechzahl in Luft zu: \(n_L=1+\frac{38\cdot\lambda}{l}=1,00029\)
Hinweis: Wegen \(𝑛_L \approx 1\) ist es unerheblich, ob man für \(𝜆_0\) die Vakuumwellenlänge oder die für Luft einsetzt.
© Cornelsen Verlag GmbH, Berlin