Mechanische Schwingungen
Aufgabe 1
a) Beide Bewegungen sind periodisch. Die Bewegung auf der Schaukel hat zwei Umkehrpunkte und ist daher eine Schwingung, die Bewegung auf dem Karussell hat keine Umkehrpunkte und ist eine Kreisbewegung.
b) Es entsprechen einander z. B.:
| Drehbewegung: | Schwingung: |
| Drehfrequenz \(\omega\) (Winkelgeschwindigkeit) | Kreisfrequenz \(\omega\) |
| Radius \(r\) | Amplitude \(s_{\rm max}\) |
| Bahngeschwindigkeit \(v\) | Maximalgeschwindigkeit \(v_{\rm max}\) |
Aufgabe 2
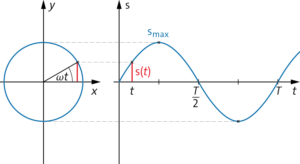
An eine Kreisscheibe wird ein Pfropfen befestigt (man kann sich auch ein Riesenrad oder ein anderes drehendes System vorstellen). Die Scheibe wird mit einem Motor in eine gleichförmige Rotation gesetzt. Das Federpendel hängt an so auf, dass sich der Pendelkörper in seiner Gleichgewichtslage in Höhe der Drehachse M des Motors befindet. Mit einer Lampe parallel zur Kreisebene wird der Schatten an eine Wand geworfen. Das Federpendel wird nun so weit nach unten ausgelenkt, dass der Umkehrpunkt in Höhe des tiefsten Punkt des Pfropfens sich befindet. Die Drehzahl des Motors wird so eingestellt, dass die Umlaufdauer des Pfropfens und die Periodendauer des Pendels gleich sind. Den Pendelkörper lässt man in dem Moment los, in dem der Pfropfen den tiefsten Punkt erreicht hat.
Die Schwingungsdauer der Feder kann nicht modifiziert werden, daher muss die Frequenz der Kreisbewegung am Motor reguliert werden. Der Radius der Kreisscheibe ist meist weniger variabel. Dagegen kann die maximale Auslenkung der Feder leicht angepasst werden.
Aufgabe 3
Alltag: Arme schwingen beim Gehen, ein umgedrehter Deckel wackelt hin und her, …
Technik: Uhrpendel, …
Sport: Bewegung an der Reckstange, Trapez, …
Gegenbeispiele (hier gibt es keine periodische Bewegung): Golfschwung (keine Wiederholung), schwingender Fisch an einer Angel, die eingeholt wird (veränderliche Periodendauer), Bäume im Wind (variierende Windstärke/Periodendauer), …
Aufgabe 4
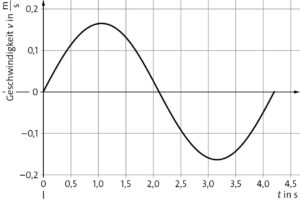
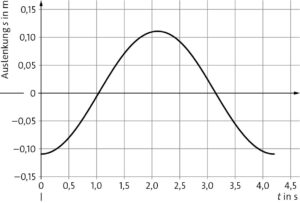
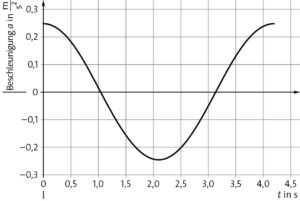
Aus der angegebenen Periodendauer ergibt sich \(𝜔 = 2𝜋/𝑇=\frac{2𝜋}{\rm 4,2\,s}= 1,496\,{\rm Hz}\) und so: \(v_{\rm max} = s_{\rm max}\cdot 𝜔 = 0,11\,{\rm m}\cdot 1,496\,{\rm Hz} = 0,165\,\frac{\rm m}{\rm s}\) sowie \(a_{\rm max}= s_{\rm max} \cdot \omega^2 = 0,11\,{\rm m}\cdot (1,496\,{\rm Hz})^2 = 0,246\,\frac{\rm m}{\rm s^2}\) .
Die Bewegung wird aus dem „unteren“ (negativ gezählten) Umkehrpunkt gestartet. Also ist:
\(𝑠(𝑡) = − s_{\rm max}\cdot \cos (𝜔 \cdot 𝑡)\)
\(𝑣(𝑡) = s_{\rm max}(𝑡) = v_{\rm max}\cdot \sin (𝜔 \cdot 𝑡)\)
\(𝑎(𝑡) = \dot v(𝑡) = a_{\rm max}\cdot \cos (𝜔 \cdot 𝑡)\)
Fadenpendel
Aufgabe 1
a) \(T=2\pi\cdot\sqrt{\frac{l}{g}}\Rightarrow g=\frac{4\pi^2}{T^2}\cdot l\approx 9,8\,{\rm s}\)
b) Die Kleinwinkelnäherung gilt im Bogenmaß. Dabei ergibt sich durch Ausprobieren, dass die Abweichung für Winkel bis \(𝛼 = 0,24\) weniger als \(1\,%\) beträgt. Im Gradmaß beträgt der Winkel damit fast 14°.
Aufgabe 2
a) Die Amplitude ist \(A=0,15\,{\rm m}\) und die Periodendauert ist wegen \(\omega=\frac{2\pi}{T}\) gleich \(T=1,5\,{\rm s}\).
b) Es handelt sich um eine Kosinusfunktion. Für diese gilt \(\cos(0)=1\) und deshalb \(x(0)=0,15\,{\rm m}=15\,{\rm cm}=A\). Die Schwingungsgleichung und damit die Messung startet also bei der maximalen Auslenkung.
c) Es gilt: \(T=2\pi\cdot\sqrt{\frac{l}{g}}\Rightarrow l=\frac{T^2\cdot g}{4\pi^2}=55,9\,{\rm cm}\)
Aufgabe 3
a) Die gesamte Ableseungenauigkeit beim Bestimmen der Zeit ist unabhängig von der Anzahl der verstrichenen Perioden. Die Ableseungenauigkeit für eine Periodendauer wird kleiner, wenn man mehrere Perioden stoppt. Sie ergibt sich aus der gesamten Ableseungenauigkeit geteilt durch die Anzahl der Perioden.
b) Es gilt: \(T=2\pi\cdot\sqrt{\frac{l}{g}}\Rightarrow l=\frac{T^2\cdot g}{4\pi^2}=24,8\,{\rm cm}\)
c) Ein erhöhter Ortsfaktor sorgt bei einem ausgelenkten Fadenpendel und sonst unveränderten Verhältnissen für eine stärkere Rückstellkraft und damit eine Verkürzung der Zeit vom Loslassen bis zum Durchgang durch die Gleichgewichtslage. Es müsste also gelten: Je höher \(g,\) desto geringer \(𝑇\). Es ist dagegen nicht möglich, auf eine einen genaueren Zusammenhang zu schließen, denn es gibt viele Funktionen, die streng monoton fallen.
Federpendel
Aufgabe 1
a) Es gilt: \(T=2\pi\cdot\sqrt{\frac{m}{D}}\approx 0,20\,{\rm s}\)
b) Mathematische Begründung:
Die Periodendauer eines Federpendels ist unabhängig vom Ortsfaktor \(𝑔\). Damit würde sich seine Periodendauer auf dem Mond nicht ändern, da \(𝑚\) und \(𝐷\) nicht verändert werden.
Physikalische Begründung:
Die Gravitation beeinflusst zwar die Ruhelage \(𝑠_0\) des Federpendels, aber nicht die Schwingung um die Ruhelage herum. Diese wird durch die Rückstellkraft \(𝐹_{\rm rück} = 𝑚 \cdot 𝑔 − 𝐷 \cdot 𝑠 = 𝐷 \cdot (𝑠_0 − 𝑠) = 𝐷 \cdot 𝑦\) bestimmt, bei gleicher Amplitude \(𝑦\) also durch die unveränderte Federkonstante. Die Periodendauer bleibt gleich.
Hinweis: Im Gegensatz dazu sinkt die Periodendauer beim Fadenpendel auf dem Mond um einen Faktor von etwa \(\sqrt{\frac{1}{6}}\approx 0,41\) gegenüber der Periodendauer auf der Erde.
c) \(s(t)=3\,{\rm cm}\cdot \cos\left(\frac{2\pi}{\rm 0,2\,s}\cdot t \right)\)
Aufgabe 2
a) Pendel 1 schwingt am langsamsten, Pendel 2 wurde am weitesten ausgelenkt und Pendel 3 schwingt gedämpft:
Pendel 1: \(T=1,5\,{\rm s}\); \(s_{\rm max}= 2,5\,{\rm cm}\)
Pendel 2: \(T=1,0\,{\rm s}\); \(s_{\rm max}= 3,0\,{\rm cm}\)
Pendel 3: \(T=0,5\,{\rm s}\); \(s_{\rm max}= 2,0\,{\rm cm}\)
b) Pendel 1 hat die weichste Feder oder die größte Masse. Bei Pendel 3 schwingt der Pendelkörper im Wasser. Die Messung beginnt für Pendel 1 und 3 bei maximaler Auslenkung. Pendel 2 dagegen erst beim Durchgang durch die Ruhelage.
Aufgabe 3
a) Aus der oberen Abbildung lässt sich ablesen, dass für 4,5 vollständige Schwingungen eine Zeit von 4,4 s benötigt wird. Für die Schwingungsdauer ergibt sich daher: \(T=\frac{\rm 4,4\,s}{4,5}\approx 0,98\,{\rm s}\)
Damit ergibt sich die Frequenz zu \(f=\frac{1}{T}\approx 1,02\,{\rm Hz}\).
b) Für die Schwingungsdauer des Federpendels gilt \(T=2\pi\cdot\sqrt{\frac{m}{D}}\), also folgt für die Federkonstante:
\(D=\frac{4\pi^2\cdot m}{T^2}\approx 10,7\,\frac{\rm N}{\rm m}\)
c) Für die Schwingung des ungedämpften Federpendels lässt sich über folgende Funktion die Auslenkung beschreiben:
\(s(t)=s_{\rm max}\cdot \sin\left(\frac{2\pi}{T}\cdot t\right)=7,6\,{\rm cm}\cdot \sin\left(\frac{2\pi}{\rm 0,98\,s}\cdot t\right)\)
d) Nach 3,0 s ergibt sich die Auslenkung \(s(3,0\,{\rm s}) \approx 2,9\,{\rm cm}\). Dies passt zu den Werten in Abbildung 3.
Aufgabe 4
a) Es ergeben sich die Einhüllenden in der Abbildung.
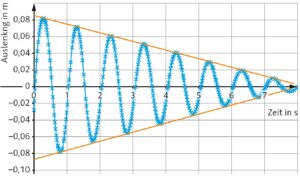
b) Für die Steigung m der oberen Einhüllenden gilt:
\(m=\frac{s(4,2)\,{\rm s}-s(0\,{\rm s})}{4,2\,{\rm s}}=\frac{4,0\,{\rm cm}-8,5\,{\rm cm}}{4,2\,{\rm s}}\approx -1,07\,\frac{\rm cm}{\rm s}\)
Für die obere Einhüllende folgt daraus:
\(s_{\rm max}(t)=-1,07\,\frac{\rm cm}{\rm s}\cdot t+8,5{\rm cm}\)
Anwendung Hemmpendel
Aufgabe 1
Von links kommend schwingt das Pendel mit der vollen Fadenlänge \(l_2\). Durch den Stift wird die Schwingung gehemmt. Das Pendel schwingt rechts mit der verkürzten Länge \(l_2\) weiter. Folglich ist auch die Amplitude rechts kleiner als links.
Aufgrund des Energieerhaltungssatzes erreicht das Pendel auf beiden Seiten die gleiche Höhe. Die potentiellen Energien (Lageenergien) auf beiden Seiten sind wegen des Energieerhaltungssatzes gleich.
Eine halbe Schwingung dauert die linke Hälfte der Schwingung wegen der größeren Fadenlänge länger als die andere. Für die Gesamtperiodendauer \(T_{\rm ges}\) des Hemmpendels addieren sich beide Halbperioden:
\(T_{\rm ges}=\frac{T_1}{2}+\frac{T_2}{2}=\pi\cdot\sqrt{\frac{l_1}{g}}+\pi\cdot\sqrt{\frac{l_2}{g}}\)
Die kürzere Periodendauer und die kleinere Amplitude beim Ausschlag nach rechts führt zu einer kürzeren und kleineren Hälfte des Sinusgraphen oberhalb der Zeitachse. In der Gleichgewichtslage geht die eine Schwingungshälfte in die andere über. An dieser Stelle liegt ausschließlich kinetische Energie vor. Sie und damit der Betrag der Geschwindigkeit sind von beiden Seiten kommend gleich groß.
Aufgabe 2
Bedingt durch den gleichen maximalen Geschwindigkeitsbetrag und wegen der kürzeren Periodendauer verläuft der Graph im \(t\)-\(v\)-Diagramm auf der gehemmten Seite steiler. Die Steigung (über Steigungsdreieck zu ermitteln) entspricht der Beschleunigung und diese ist zu der Rückstellkraft proportional. Folglich ist die maximale Rückstellkraft auf der rechten Seite größer. Diese Aussage ergibt sich auch, wenn man in den Wendepunkten durch Kräftezerlegung Gewichtskraft die Rückstellkraft konstruiert.
Aufgabe 3
Aufgrund der Starthöhe oberhalb des Hindernisses schwingt der Pendelkörper auf der gehemmten Seite so weit, dass Auslenkungswinkel oberhalb von 90° erreicht werden. Bei der anschließenden Rückwärtsbewegung ist der Pendelkörper dann nicht mehr durch den Faden geführt, sondern fällt frei, bis der Faden wieder straff gespannt ist. Damit sind Hin- und Rückweg unterschiedlich, anders als bei Schwingungen.
Resonanz und Dämpfung
Aufgabe 1
Resonanz bedeutet: Wird ein System in seiner Eigenfrequenz angeregt, wird maximale Energie übertragen und die Amplitude ist am größten.
Erläuterung: Ein schwingungsfähiges System lässt sich von außen durch einen Erreger periodisch zum Mitschwingen anregen. Die Anregung des Systems erfolgt mit einer bestimmten Frequenz auf mechanische oder elektrische Weise. Dabei wird dem System Energie zugeführt. Je näher die Anregungsfrequenz \(f_a\) des Erregers an der Eigenfrequenz \(f_0\) des schwingenden Systems ist, umso mehr schaukelt sich die Amplitude \(s_{\rm max}\) auf. Der Körper bewegt sich im Resonanzfall mit einer Viertelperiode der erregenden Schwingung hinterher.
Aufgabe 2
Beispiel Tacoma Narrows Bridge:
Ein nicht zu starker Wind ließ die Tacoma Narrows Bridge aufschaukeln. Der Wind führte dazu, dass die Brücke in ihrer Eigenfrequenz zu schwingen begann. Die kinetische Energie der Brücke konnte zudem nicht schonend umgewandelt werden. Sie wurde immer größer, bis die Brücke zerbrach.
Aufgabe 3
Die Amplitude bleibt gering, wenn
– die Dämpfung groß ist,
– die Erregerfrequenz deutlich von der Eigenfrequenz abweicht.
Aufgabe 4
a) Durch Ablesen aus dem Diagramm ergibt sich: \(s_0=0\,{\rm cm}\); \(T=2,0\,{\rm s}\)
b) Es gilt \(\omega =\frac{2\pi}{T}=3,14\,{\rm Hz}\). Mit \(\omega=\frac{D}{m}\) erhält man:
\(D=\omega^2\cdot m=2,96\,\frac{\rm N}{\rm m}\)
c)
| \(i\) | 1 | 2 | 3 | 4 | 5 | 6 |
| \(s_i\) in cm | 10 | 6,6 | 4,5 | 3,2 | 2,0 | 1,3 |
| \(\frac{s_i}{s_{i+1}}\) | 1,5 | 1,5 | 1,4 | 1,6 | 1,5 | – |
Im Rahmen der Ablesegenauigkeit bleibt das Verhältnis konstant. Analog für Tiefpunkte.
Elektromagnetischer Schwingkreis
Aufgabe 1
a)
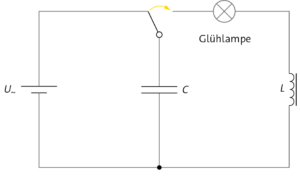
b) Der Schwingkreis mit Kondensator und Spule wird durch eine Wechselspannung zu einer erzwungenen Schwingung angeregt. Abhängig von \(L\) und \(C\) hat der Schwingkreis eine Eigenfrequenz f0 die sich mit der Thomsonschen Schwingungsgleichung ermitteln lässt. Ist die Frequenz der anregenden Spannung gleich groß, liegt der Resonanzfall vor. Maximale Energie fließt in den Schwingkreis. Die Lampe leuchtet maximal.
c) Die Thomsonsche Gleichung lautet: \(f= \frac{1}{2π\cdot\sqrt{L\cdot C}}\)
Wird die Kapazität bzw. die Induktivität größer, so wird die Frequenz des Schwingkreises kleiner. Das heißt, ein Kondensator, der viele Ladungsträger speichern kann bzw. eine Spule, die eine hohe Selbstinduktion aufweisen, hemmen den Schwingkreis.
Aufgabe 2
a)
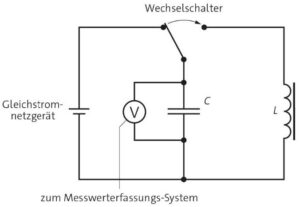
Sobald der geladene Kondensator durch das Umlegen des Wechselschalters mit der Spule verbunden ist, beginnt er sich zu entladen. Bei diesem Entladungsvorgang gibt es einen Strom und insbesondere eine Stromstärkenänderung in der Spule. Durch die damit verbundene Änderung des magnetischen Flusses in der Spule wird eine Spannung induziert, die nach der Lenzschen Regel ihrer Ursache entgegenwirkt (Selbstinduktion).
Durch die Induktionsspannung steigt die Stromstärke ohne Sprung von 0 A aus an.
Wenn der Kondensator entladen ist, gibt es keinen Antrieb mehr für den elektrischen Strom. Die Selbstinduktion sorgt nun ähnlich wie beim Ausschaltvorgang der Spule dafür, dass dieser Strom wieder ohne Sprung abnimmt. Da die Stromrichtung gleich bleibt, lädt sich dadurch der Kondensator mit im Vergleich zum Anfangszustand umgekehrten Vorzeichen wieder auf. Durch die zunehmende Ladung nimmt die Stromstärke immer weiter ab, bis sie auf 0 A zurückgeht und der Kondensator genau so geladen ist wie zu Beginn, nur mit umgekehrten Vorzeichen. Daher läuft der Vorgang in gleicher Weise wieder ab, sodass sich insgesamt eine elektromagnetische Schwingung ergibt.
b) Mit der Thomson-Gleichung \(𝑇 = 2π\cdot\sqrt{L\cdot C}\) lassen sich die Periodendauern berechnen:
\(C=25\,{\rm µF}:\ T=0,70\,{\rm s}\)
\(C=50\,{\rm µF}:\ T=0,99\,{\rm s}\)
\(C=100\,{\rm µF}:\ T=1,4\,{\rm s}\)
Der 50-μT-Kondensator ist geeignet, weil dieser die passende Periodendauer liefert.
c) \(E_{\rm el}=\frac{1}{2}\cdot C\cdot U_{\rm max}^2=\frac{1}{2}\cdot 50\,{\rm µF}\cdot (10\,{\rm V})^2=2,5\,{\rm mJ}\)
d) Wenn die Stromstärke maximal ist, ist die Energie des elektrischen Felds vom Beginn komplett in Energie des magnetischen Felds umgewandelt worden:
\(\frac{1}{2}\cdot C\cdot U_{\rm max}^2=\frac{1}{2}\cdot L\cdot I_{\rm max}^2\Rightarrow I_{\rm max}=U_{\rm max}\cdot \sqrt{\frac{C}{L}}\approx 3,2\,{\rm mA}\)
e)
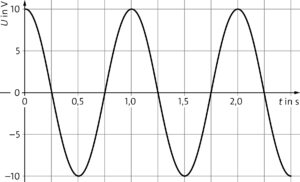
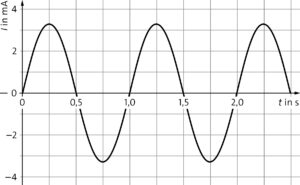
Die Periodendauer ist bei der Kombination aus 500 und 50 μF im Bereich der Zeichengenauigkeit 1,0 s. Die Scheitelwerte für Spannung und Stromstärke wurden in c) und d) bestimmt. Wenn man für \(t =0\,{\rm s}\) mit einem voll geladenen Kondensator beginnt, ist die Spannung kosinusförmig. Die Phasenverschiebung bei der Stromstärke ergibt sich durch die Selbstinduktion der Spule.
Funktionsgleichung: Es handelt sich um eine harmonische Schwingung mit konstanter Periodendauer \(T=1,0\,{\rm s}\):
\(U(t)=10\,{\rm V}\cdot \cos\left(\frac{2\pi}{\rm 1,0\,s}\cdot t\right)\)
\(U(t)=3,2\,{\rm mA}\cdot \cos\left(\frac{2\pi}{\rm 1,0\,s}\cdot t\right)\)
f)
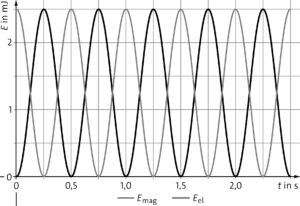
Die Periodendauer ist beim \(E\)-\(t\)-Diagramm halb so groß wie beim \(U\)-\(t\)- bzw. \(I\)-\(t\)-Diagramm. Die Energieformen variieren nur zwischen \(0\,{\rm mJ}\) und \(2,5\,{\rm mJ}\), während \(U\) und \(I\) positive und negative Werte annehmen. (Das ergibt sich ebenso wie die Phasenlage aus der jeweils quadratischen Abhängigkeit der Energieformen von \(U\) und \(I\).) Der Maximalwert für beide Energieformen beträgt jeweils \(2,5\,{\rm mJ}\) (s. Teilaufgabe c), während die Amplituden in e) unterschiedlich sind, da es sich um unterschiedliche Größen handelt.
Aufgabe 3
a) Ihren Amplitudenwert erreicht die Spannung, wenn die gesamte Energie des Schwingkreises im elektrischen Feld gespeichert ist. Durch den Widerstand (vor allem den des Spulendrahts) gibt der Schwingkreis thermisch Energie ab, sodass die Gesamtenergie und damit die Spannungsamplitude abnimmt.
b) Aus dem Diagramm kann man ablesen, dass zu Beginn \(U_{\rm max}= 10\,{\rm V}\) ist und nach einer Periodendauer \(U_{\rm max}= 7,0\,{\rm V}\). Für das Verhältnis der beiden damit verbundenen Energien gilt: \(\frac{E_1}{E_0}=\frac{\frac{1}{2}\cdot C\cdot U_1^2}{\frac{1}{2}\cdot C\cdot U_0^2}=\frac{U_{\rm max,1}^2}{U_{\rm max,0}^2}=49\,\%\)
Das heißt die Energie hat um \(100\,\%-49\,\%=51\,\%\) abgenommen.
c) Eine lineare Abnahme lässt sich ausschließen, da sonst die Amplituden im positiven Bereich auf einer Geraden liegen müssten. Wenn es sich um eine exponentielle Abnahme handelt, muss das Verhältnis \(\frac{𝐸_𝑖}{𝐸_{𝑖−1}}\) immer gleich bleiben, was der Fall ist:
| \(i\) | 0 | 1 | 2 | 3 | 4 |
| \(U_{\text{max},i}\) in V | 10 | 7,0 | 5,0 | 3,5 | 2,5 |
| \(\frac{E_i}{E_{i+1}}\) | – | 49 % | 51 % | 49 % | 51 % |
d) Nach 4,0 s sind 5,25 Periodendauern vergangen: \(T=\frac{\rm 4,0\,s}{4,25}\approx 9,4\,{\rm s}\)
Aufgabe 4
a) Da \(𝑇\sim\sqrt{C}\) und die gemessene Periodendauer kleiner als 1,0 s ist, genügt es zur Überprüfung den kleinstmöglichen Wert für die Kapazität, 45 μF, in die Thomson- Gleichung einzusetzen: \(𝑇 = 2𝜋 \cdot \sqrt{500\,{\rm H}\cdot 45\,{\rm μF}}\approx 0,94\,{\rm s}\). Bei maximaler Abweichung der Kapazität vom Nennwert nach unten könnte die gemessene Periodendauer gerade noch erklärt werden.
b) Aufgrund der Thomson-Gleichung gilt für die Frequenz \(f= \frac{1}{2π}\cdot\sqrt{\frac{1}{L\cdot C}}\). Der angegebene Zusammenhang zeigt, dass die Frequenz durch den Widerstand abnimmt, d. h., die Periodendauer müsste größer sein als 1,0 s. Das ist nicht der Fall, d. h., der Widerstand kann die Abweichung also nicht erklären. (Ein Einsetzen der Werte zeigt, dass der Widerstand ohnehin vernachlässigbar ist.)
© Cornelsen Verlag GmbH, Berlin