Elektrisches Wirbelfeld
Aufgabe 1
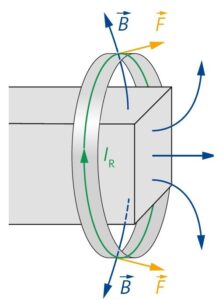
Wenn der Ring durchtrennt wird, kommt im Ring kein Strom mehr zustande. Deswegen kann im Magnetfeld keine Kraft mehr auf ihn ausgeübt werden und der Ring wird nicht abgestoßen oder angezogen.
Aufgabe 2
Aufgabe 3
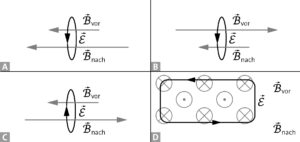
a) Wenn man den Nordpol auf den Ring zubewegt, zeigt \(\frac{\Delta\vec{B}}{\Delta t}\) nach rechts, sodass im Ring ein Strom induziert wird, der aufgrund der Linken-Hand-Regel die eingezeichnete Richtung hat. Da ein Teil der Feldlinien nach außen weisen, gibt es im Magnetfeld eine Kraft auf den Ring nach rechts (Drei-Finger-Regel rechts). Zieht man den Magneten zurück, ist \(\frac{\Delta\vec{B}}{\Delta t}\) nach links gerichtet, sodass die Kraft auf den Magneten nach links zeigt.
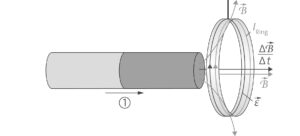
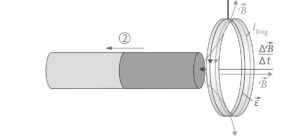
b) Wenn man den Magneten auf den Ring zu bewegt, wird durch die Flussdichtezunahme ein Strom im Ring induziert. Der Strom ist so gerichtet, dass er der Flussdichtezunahme entgegenwirkt und deshalb zu einer Abstoßung des Rings führt. Beim Wegziehen des Magneten nimmt die Flussdichte ab, sodass der Ringstrom nun so gerichtet sein muss, dass er diese Abnahme verlangsamt. Das führt dazu, dass der Ring mitgezogen wird.
Aufgabe 4
a) Die Feldspule erzeugt ein Feld \(B_1(t) = B_{\rm max}\cdot \sin(\omega \cdot t)\). Nach dem Induktionsgesetz entsteht in der Induktionsspule folgende Spannung: \(U_i(t) = –N_2 \cdot A \cdot\dot{B}_1(t)\).
Wir leiten ab: \(U_i(t) = –N_2 \cdot A \cdot B_{\rm max} ⋅ \cos(ω \cdot t)\). Diese Spannung \(U_i\) treibt in der Induktionsspule einen Strom \(I_2\) an. Wenn wir keine weiteren Induktionseffekte berücksichtigen, dann ist \(I_2\) proportional zu \(U_i\) und somit zu \(–\cos(ω \cdot t)\). Somit erzeugt \(I_2\) ein Feld \(B_2\), das auch proportional zu \(–\cos(ω \cdot t)\) ist. Dieses Feld \(B_2\) eilt also dem Feld \(B_1\) der Hauptspule um \(π/2\) hinterher.
b) Im Bezugssystem des Drehfeldes hat die Aluminiumdose eine Relativgeschwindigkeit. Das erzeugt bremsende Wirbelströme. Dadurch wird die Relativgeschwindigkeit null und das Teelicht dreht sich mit dem Wirbelfeld mit.
| Spaltmotor: | Modellmotor: |
| Hauptspule | Zwei Spulen am Netzgerät |
| kurzgeschlossene Spule | kurzgeschlossene Spule |
| Drehfeld \(B_1(t)+B_2(t)\) | Drehfeld \(B_1(t)+B_2(t)\) |
| Rotor | Teelicht |
c)
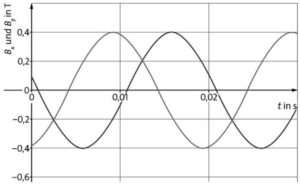
Die Abbildung stellt den Zeitverlauf der Komponenten des Drehfeldes dar.
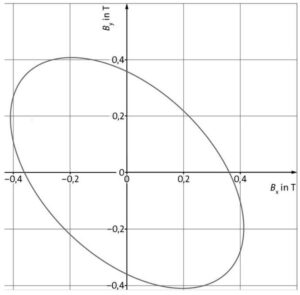
Die Abbildung stellt das Drehfeld in der Ebene dar. Die Abbildungen zeigen, wie sich das Drehfeld in der Ebene und abhängig von der Zeit entwickelt.
d) Im Bezugssystem des Drehfeldes hat die Aluminiumdose eine Relativgeschwindigkeit, die durch Wirbelströme abgebremst wird, bis sich das Teelicht mit dem Wirbelfeld dreht.
e) Der Stator erzeugt ein Drehfeld und sollte daher ein Elektromagnet sein. Der Rotor arbeitet nach dem Prinzip der Wirbelstrombremse ohne Ferromagnetismus. Somit werden keine Permanentmagneten benötigt.
Lenzsche Regel
Aufgabe 1
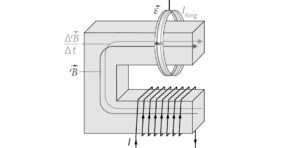
Beim Einschalten wird durch die Zunahme der Flussdichte im Ring ein elektrischer Strom induziert. Der Strom im Ring muss aufgrund der Lenzschen Regel so gerichtet sein, dass er ein Magnetfeld hat, dessen Flussdichte die Zunahme abschwächt. Das ist der Fall, wenn die Richtung des Ringstroms entgegensetzt zur Richtung des Spulenstroms ist. Die Abstoßung ergibt sich dann wie in der Abbildung.
Beim Ausschalten muss das Magnetfeld des Ringstroms so gerichtet sein, dass Abnahme der Flussdichte des Spulenfeldes abschwächt.
Aufgabe 2
a)
Im Bereich des Rings verläuft ein Teil der Feldlinien des Magnetfelds radial nach außen. Dadurch ergibt sich durch den Ringstrom aufgrund der Drei-Finger-Regel (rechts) eine Kraft im Magnetfeld nach rechts, sodass der Ring kurz nach rechts beschleunigt wird.
b)
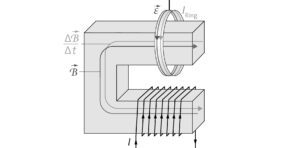
Durch die Remanenz des Eisenkerns gibt es auch nach dem Ausschalten noch ein Magnetfeld, von dem ein Teil (wie in Teilaufgabe b beschrieben) nach außen verläuft. Aufgrund der umgedrehten Stromrichtung im Ring ist die Kraft auf den Ring nun nach links gerichtet.
c) Durch den geschlossenen Eisenkern verlaufen nun fast alle Feldlinien des Magnetfeldes im Eisenkern, sodass es außerhalb nur ein extrem schwaches Feld gibt, dessen Feldlinien nach außen zeigen. Dadurch ist die Kraft auf den Ring so klein, dass er sich nicht mehr bewegt.
Elektromagnetische Induktion
Aufgabe 1
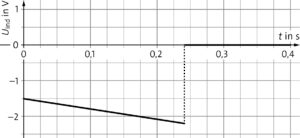
a) Beim Ansteigen benötigt die Flussdichte eine dreimal so große Zeitspanne wie beim Abnehmen (Abb. 4A), d. h., der Betrag von \(\frac{\Delta B}{\Delta t}\) ist beim Abnehmen drei Mal so groß wie beim Ansteigen und hat ein entgegengesetztes Vorzeichen. In beiden Phasen ist \(\frac{\Delta B}{\Delta t}\) auch konstant. In Abbildung 4B erkennt man, dass diese Eigenschaften von \(\frac{\Delta B}{\Delta t}\) auch für \(U_{\rm ind}\) zutreffen.
b) Für die Flussänderung gilt beim Abnehmen:
\(\frac{\Delta \phi}{\Delta t}=A\cdot \frac{\Delta B}{\Delta t}=-1,25\cdot10^{-5}\,\frac{\rm T\cdot m^2}{\rm s}\)
Aus dem Induktionsgesetz ergibt sich damit die Windungszahl:
\(n=-\frac{U_{\rm ind}}{\Delta \phi/\Delta t}=360\)
Aufgabe 2
a) Für \(0\,{\rm s} ≤ t < 2\,{\rm s}\) ist die Steigung im \(B(t)\)-Diagramm größer als für \(2\,{\rm s} ≤ t < 4\,{\rm s}\) . Dementsprechend ist \(\frac{\Delta\phi}{\Delta t}\) größer und damit wegen des Induktionsgesetzes die Induktionsspannung zu Beginn größer. Für \(t ≥ 6\,{\rm s}\) ist die Steigung negativ. Entsprechend ändert sich auch das Vorzeichen der Induktionsspannung.
b)
\(0\,{\rm s} ≤ t < 2\,{\rm s}\): \(\frac{\Delta B}{\Delta t}=\frac{\rm 40\,mT}{\rm 2,0\,s}=20\,\frac{\rm mT}{\rm s}\)
\(2\,{\rm s} ≤ t < 4\,{\rm s}\): \(\frac{\Delta B}{\Delta t}=\frac{\rm 20\,mT}{\rm 2,0\,s}=10\,\frac{\rm mT}{\rm s}\)
\(4\,{\rm s} ≤ t < 6\,{\rm s}\): \(\frac{\Delta B}{\Delta t}=0\,\frac{\rm mT}{\rm s}\)
\(6\,{\rm s}\le t\): \(\frac{\Delta B}{\Delta t}=\frac{\rm -30\,mT}{\rm 1,0\,s}=-30\,\frac{\rm mT}{\rm s}\)
c)

d) Beispiele:
- In der gleichen Zeitspanne die Flussdichte um den
dreifachen Betrag verändern - die Flussdichte in einem Drittel der Zeitdauer um den
gleichen Betrag ändern - die Windungszahl verdreifachen
- die Querschnittsfläche verdreifachen
- oder verschiedene Kombinationen der angegebenen
Möglichkeiten
In der vorgegebenen Situation ergibt sich aus dem Induktionsgesetz \(U_{\rm ind}(t) = −n \cdot \dot{\phi(t)} = −n \cdot A \cdot \frac{\Delta B}{\Delta t}\). Die Induktionsspannung ist also (wenn man alle anderen Größen konstant hält) proportional zur Windungszahl \(n\), zur Querschnittsfläche \(A\), zur Flussdichteänderung \(\Delta B\) und antiproportional zur Zeitspanne \(\Delta t\). Daraus ergeben sich die in genannten Möglichkeiten.
Aufgabe 3
a) Wenn die untere Kante des Rahmens sich im Magnetfeld bewegt, bewegen sich die frei beweglichen Elektronen im Draht mit. Daher wirkt auf sie eine Lorentzkraft aufgrund der Drei-Finger-Regel (links) nach rechts. Durch die Ladungsverschiebung entsteht ein elektrisches Feld, sodass sich bei den Elektronen ein Kräftegleichgewicht zwischen Lorentzkraft und elektrischer Kraft einstellt und zwischen P und Q eine Spannung entsteht. Wenn der Rahmen sich ganz im Magnetfeld befindet, ist die Situation in der oberen Kante genau so wie in der unteren Kante. In diesem Fall gibt es zwischen P und Q keine Potenzialdifferenz, sodass auch keine Spannung gemessen wird.
b)
(i) Die Anzahl der gezeichneten Feldlinien nimmt während des Eintauchens zu, d. h., der Daumen der linken Hand zeigt senkrecht aus der Zeichenebene hinaus und die Finger zeigen gegen den Uhrzeigersinn. Daher ist Q positiv und P negativ.
(ii) Die Lorentzkraft auf die Elektronen verschiebt diese aufgrund der Drei-Finger-Regel nach rechts. Deswegen ist P negativ und Q positiv.
c) Während des Eintauchens wird durch die Lorentzkraft auf die Elektronen ein Strom gegen den Uhrzeigersinn im Drahtrahmen induziert. In der unteren Kante verläuft dieser nach links, sodass auf den Draht dort aufgrund der Drei-Finger-Regel (rechts) eine Kraft gegen die Bewegungsrichtung ausgeübt wird. Wenn keine äußere Kraft auf den Drahtrahmen ausgeübt wird, wird er daher abgebremst. Durch eine nach unten gerichtete äußere Kraft muss man dafür sorgen, dass der Rahmen sich im Kräftegleichgewicht befindet und sich somit mit konstanter Geschwindigkeit weiter bewegt. In den Abschnitten der linken und rechten Rahmenkante, die sich im Magnetfeld befinden, sind die Stromrichtungen entgegengesetzt. Die Kräfte auf diese Abschnitte sind betragsgleich und entgegengesetzt gerichtet und heben sich daher auf.
Wenn der Drahtrahmen ganz im Magnetfeld ist, kommt es in der oberen und der unteren Kante zwar zu einer Ladungsverschiebung, aber es gibt keinen Strom durch den gesamten Rahmen. Daher gibt es keine Kraft auf den Drahtrahmen, die durch eine äußere Kraft ausgeglichen werden müsste.
Aufgabe 4
a)
(i) Beim Eintauchen ändert sich der magnetische Fluss in der Spule, sodass eine Spannung induziert wird.
(ii) In der rechten Seite der Spule werden im Draht die frei beweglichen Elektronen durch das Magnetfeld mitbewegt, sodass auf sie eine Lorentzkraft wirkt, die für eine Ladungsverschiebung sorgt. Mit dieser Ladungsverschiebung ist ein elektrisches Feld und damit eine elektrische Spannung, die Induktionsspannung verbunden.
b) Da die Geschwindigkeit des Wagens aufgrund der Beschleunigung immer weiter zunimmt, nimmt auch die Änderungsrate des magnetischen Flusses und damit die Induktionsspannung während des Eintauchens zu.
c) \(U_{\rm ind}=-n\cdot B\cdot d\cdot v_1=-1,5\,{\rm V}\)
d) Wenn die Beschleunigung auch vor dem Eintauchen konstant ist, ist der Wagen \(\Delta t_1=\frac{v_1}{a}=0,5\,{\rm s}\) vorher und \(\Delta s_1=\frac{v_1^2}{2a}=0,125\,{\rm m}\) entfernt gestartet. Bei \(\Delta s_2=0,275\,{\rm m}\) ist die Spule vollständig eingetaucht. Seit dem Start sind also \(\Delta t_2=\sqrt{\frac{2\cdot \Delta s_2}{a}}\approx 0,74\,{\rm s}\) vergangen, d. h. das geschieht zum Zeitpunkt \(t_2\approx 0,14\,{\rm s}\). Zu diesem Zeitpunkt hat der Wagen eine Geschwindigkeit von \(v_2=\sqrt{2a\cdot \Delta s_2}\approx 0,74\,\frac{\rm m}{\rm s}\). Entsprechend wird eine Spannung von \(U_{\rm ind}=-n\cdot B\cdot d\cdot v_2\approx-2,22\,{\rm V}\) induziert.
Aufgabe 5
a) Durch das Verbinden der Anschlüsse gibt es einen geschlossenen Stromkreis, sodass ein Strom induziert werden kann. In der rechten Kante der Spule zeigt die Stromrichtung dabei nach oben (Linke-Hand-Regel), sodass die Drahtstücke in dieser Kante im Magnetfeld eine Kraft entgegen die Bewegungsrichtung erfahren (Drei-Finger-Regel, rechts). Da diese Kraft \(\vec{F_l}\) entgegengesetzt zur Hangabtriebskraft \(\vec{F_H}\) ist, gibt es für die resultierende Kraft \(\vec{F_{\rm res}}\) auf den Wagen während des Eintauchens drei Möglichkeiten:
(i) \(F_l<F_H\), also \(\vec{F_{\rm res}}\) zeigt zeigt weiterhin nach rechts, hat aber einen kleineren Betrag, d. h., die Beschleunigung ist kleiner.
(ii) \(F_l=F_H\), also es herrscht Kräftegleichgewicht und die Geschwindigkeit bleibt konstant.
(iii) \(F_l>F_H\), also \(\vec{F_{\rm res}}\) zeigt nach links, d. h., der Wagen wird abgebremst.
b) Für die Hangabtriebskraft gilt \(F_H = m\cdot a_0 = 0,10\,{\rm N}\).
Die Kraft auf die rechte Kante berechnet sich zu \(F_l=n\cdot B\cdot I\cdot d=n\cdot B\cdot\frac{U_{\rm ind}}{R}\cdot d= −4,5\,{\rm N}\).
Damit ergibt sich die resultierende Kraft \(F_{\rm res} = F_H + F_l = −4,4\,{\rm N}\). Das heißt, \(F_{\rm res}\) wirkt gegen die Bewegungsrichtung und bremst so den Wagen ab.
c)
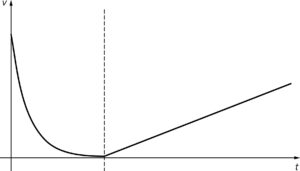
Beim Eintauchen wird der Wagen von seiner Anfangsgeschwindigkeit \(0,50\,\frac{\rm m}{\rm s}\) stark abgebremst, da \(F_l\) viel größer als \(F_H\) ist. Weil die Kraft \(F_l\) proportional zur Geschwindigkeit ist, wird sie beim Abbremsen kleiner, d. h., ihre Bremswirkung wird kleiner und die Geschwindigkeitsabnahme wird immer kleiner. Falls\(F_l\) dabei so klein wird, dass \(F_l= F_H\), herrscht Kräftegleichgewicht und die Geschwindigkeit nimmt nicht weiter ab. Wenn der Wagen komplett in das Magnetfeld eingetaucht ist, gilt \(F_{\rm res} = F_H=0,10\,{\rm N}\) und die Geschwindigkeit nimmt wegen der konstanten resultierenden Kraft so linear zu wie ohne Magnetfeld.
(Hinweis: Das \(v(t)\)-Diagramm ist nicht maßstabsgerecht.)
d) Damit der Wagen sich beim Eintauchen mit konstanter Geschwindigkeit bewegt, muss Kräftegleichgewicht herrschen: \(F_l=F_H\)
Daraus folgt: \(n\cdot B\cdot \frac{U_{\rm ind}}{R}\cdot d=m\cdot a_0 \Rightarrow \frac{n^2\cdot B^2\cdot d^2}{R}\cdot v_1=m\cdot a_0\)
\(v_1=\frac{m\cdot a_0\cdot R}{n^2\cdot B^2\cdot d^2}\approx 1,1\,\frac{\rm cm}{\rm s}\)
Induktionsherd
Es gibt insgesamt 3 Aufgaben zum Induktionsherd.
Aufgabe 1
Das Spiegelei auf dem Herd bleibt roh, während es in der Pfanne gar wird. Also bleibt der Herd kalt. Ein Vorteil ist somit, dass man keine Energie benötigt, um eine Herdplatte zu heizen. Entsprechend ist ein Nachteil, dass der Topf einen hinreichend dicken Metallboden braucht, damit die Induktionsströme gut fließen können.
Aufgabe 2
Wir ermitteln die Spannung mit dem Induktionsgesetz: \(U_{\rm ind} = –N \cdot A \cdot \dot B(t)\). Beim Ableiten mit der Kettenregel entsteht
der Faktor \(\omega\). Daher beträgt die Amplitude der Induktionsspannung: \(U_{\rm ind,max}=N \cdot A \cdot B \cdot\omega\). Wir setzen die gegebenen Größen ein und erhalten \(U_{\rm ind,max}=216\,{\rm V}\). Die LED überhitzt.
Aufgabe 3
Wir ermitteln die Spannung mit dem Induktionsgesetz \(U_{\rm ind} = –N \cdot A \cdot \dot B(t)\). Beim Ableiten mit der Kettenregel entsteht der Faktor \(\omega\). Daher beträgt die Amplitude der Induktionsspannung: \(U_{\rm ind,max}=N \cdot A \cdot B \cdot\omega\). Wir ermitteln die nötigen Größen:
Die Windungszahl ist 1. Die Fläche ist \(A=\pi\cdot r^2=0,123\,{\rm m^2}\). Wir setzen die Größen ein und erhalten: \(U_{\rm ind,max}=2,46,{\rm V}\)
Wir ermitteln die Stromstärke, welche die Begrenzung durch den Widerstand ergibt, \(I=\frac{U}{R}\) und setzen die Größen ein: \(I=1,23\,{\rm kA}\)
Generator
Aufgabe 1
a) Wenn die Spule gedreht wird, werden die beweglichen Elektronen im Draht durch das Magnetfeld bewegt. Wenn \(\alpha = 90°\) (bzw. \(270°\)) ist, bewegen sich die Elektronen orthogonal zu den Feldlinien, sodass der Betrag der Lorentzkraft maximal ist. Wenn \(\alpha = 0°\) (bzw. \(180°\)) ist, bewegen
sich die Elektronen parallel zu den Feldlinien und erfahren keine Lorentzkraft. Dazwischen gibt es einen Übergang zwischen den beiden Extremen. Entsprechend gibt es eine sich periodisch ändernde Lorentzkraft.
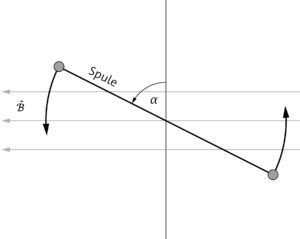
b) Auf die beiden Leitstücke parallel zur Drehachse wird durch die Drehbewegung im Magnetfeld eine Kraft ausgeübt, für die gilt \(F = B \cdot I \cdot s \cdot \sin(\alpha)\). Dabei kommt diese Kraft durch die Lorentzkraft auf die frei beweglichen Elektronen in den Leiterstücken zustande. Entsprechend wirkt die Lorentzkraft nur proportional zur Geschwindigkeitskomponente orthogonal zu den Feldlinien, d. h. \(F_L = e\cdot B \cdot v \cdot \sin(\alpha)\).
c) Durch die Lorentzkraft kommt es in jedem der beiden Leiterstücke der Länge \(l\) zu einer Ladungsverschiebung und damit zu einem elektrischen Feld. Wenn die damit verbundene elektrische Kraft auf die Elektronen im Gleichgewicht zur Lorentzkraft ist, stellt sich eine entsprechende Induktionsspannung ein: \(F_{el}=F_L \Rightarrow e\cdot E=e\cdot B\cdot v\cdot \sin(\alpha)\Rightarrow \frac{U}{l}=B\cdot v\cdot \sin(\alpha)\)
Da es zwei Leiterstücke gibt, in denen eine Spannung induziert wird, gilt für die Induktionsspannung: \(U_{\rm ind}=2\cdot l\cdot v\cdot B\cdot \sin(\alpha)\)
Der Winkel \(\alpha\) ändert sich mit der Winkelgeschwindigkeit \(\omega\), sodass sich insgesamt ergibt: \(U_{\rm ind}=2\cdot l\cdot v\cdot B\cdot \sin(\omega\cdot t)\)
d) Aus dem Induktionsgesetz ergibt sich der Zusammenhang \(U_{\rm ind}=A\cdot B\cdot \omega\cdot \sin(\omega\cdot t)\). Der Ausdruck aus c) sollte mit damit übereinstimmen, d. h., man muss zeigen, dass \(2\cdot l\cdot v\cdot B\cdot \sin(\omega\cdot t)=A\cdot B\cdot \omega\cdot \sin(\omega\cdot t)\)
\(\Leftrightarrow 2\cdot l\cdot v=A\cdot \omega\)
Für Bahn- und Winkelgeschwindigkeit gilt beim Bahnradius \(r\) der Zusammenhang \(v = \omega\cdot r\). Eingesetzt in die obere Gleichung erhält man:
\(2\cdot l\cdot \omega\cdot r=A\cdot \omega \Leftrightarrow 2\cdot r\cdot l=A\)
Der Ausdruck \((2\cdot r)\cdot l\) ist gerade der Flächeninhalt des rechteckigen Drahtrahmens, d. h., die beiden Zusammenhänge für \(U_{\rm ind}\) stimmen überein.
Aufgabe 2
a) Laut dem Induktionsgesetz wird in der Induktionsspule eine Spannung induziert, wenn sich das Magnetfeld oder die vom Magnetfeld durchsetzte Fläche ändert. Deshalb wird eine Spannung induziert, wenn sich \(B\) ändert, also für \(0\le t\le 2\,{\rm s}\) und \(t\ge 6\,{\rm s}\).
b) Da sich die Flussdichte gleichmäßig verändert, ergibt sich die Induktionsspannung über \(U_{\rm ind}=-n\cdot A\cdot\frac{\Delta B}{\Delta t}=250\cdot 20\,{\rm cm^2}\cdot \frac{\Delta B}{\Delta t}\). Die Induktionsspannung hat also für die drei Intervalle jeweils immer einen kontanten Wert:
\(0\le t\le 2\,{\rm s}\): \(U_{\rm ind}=250\cdot 20\cdot10^{-4}\,{\rm m^2}\cdot\frac{\rm 20\cdot 10^{-3}\,T}{2\,s}=3\,{\rm mV}\)
\(2< t<5\,{\rm s}\): \(U_{\rm ind}=250\cdot 20\cdot10^{-4}\,{\rm m^2}\cdot\frac{\rm 0\,T}{2\,s}=0\,{\rm mV}\)
\(5\,{\rm s\le t}\): \(U_{\rm ind}=250\cdot 20\cdot10^{-4}\,{\rm m^2}\cdot\frac{\rm -40\cdot 10^{-3}\,T}{5\,s}=-2,4\,{\rm mV}\)

c) Für eine lange Spule gilt: \(B=\mu_0\cdot\frac{n}{l}\cdot I\). Umformen nach \(I\) und Einsetzen ergibt:
\(I=\frac{B\cdot l}{\mu_0\cdot n}=\frac{\rm 20\,mT\cdot 0,6\,m}{1,256\cdot10^{-6}\,\frac{\rm V\cdot s}{\rm A\cdot m}\cdot2400}=3,98\,{\rm A}\)
Selbstinduktion
Aufgabe 1
a) Die Induktivität lässt sich mit der anfänglichen zeitlichen Ableitung und der von außen angelegten Spannung berechnen zu:
\(L=\frac{U_0}{\dot I(0\,{\rm s})}=0,125\,{\rm H}\)
Die konstante Stromstärke längere Zeit nach dem Einschalten wird nur durch die von außen angelegten Spannung und den Widerstand bestimmt, d. h. für den Widerstand ergibt sich:
\(R=\frac{U_0}{I_{\rm max}}=6,25\,{\rm \Omega}\)
b)

c) Durch die Permeabilitätszahl des Eisens erhöht sich die Induktivität der Spule. Ihr Widerstand bleibt gleich. Für die zeitliche Ableitung \(\dot I(t)\) der Stromstärke gilt \(\dot I(𝑡) = −\frac{𝑈_{\rm ind}(𝑡)}{𝐿}\). Bei gleicher Induktionsspannung ist die Steigung im \(I(t)\)-Diagramm immer kleiner, d. h. der Anstieg der Stromstärke verläuft flacher. Da sich der Widerstand nicht ändert, bleibt auch der Grenzwert \(𝐼_{\rm max}\), gegen den die Stromstärke strebt, gleich.
Aufgabe 2
a)
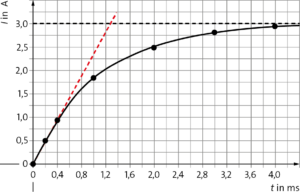
b) Der Widerstand ergibt sich aus dem Grenzwert \(I_{\rm max}\) der Stromstärke. Aus dem Diagramm liest man ab, dass \(I_{\rm max}\approx 3\,{\rm mA}\). Es gilt \(R=\frac{U}{I_{\rm max}}=\frac{\rm 12\,V}{\rm 3\,mA}=4\,{\rm k\Omega}\).
Führt man eine Kurvenanpassung durch, erhält man die Gleichung \(I(t)=3\,{\rm A}\cdot\left(1-e^{-904\,\frac{1}{\rm s}\cdot t}\right)\). Die Induktivität ergibt sich aus der Geradensteigung der Tangenten im Punkt \((0\,{\rm ms},0\,{\rm A})\) über \(L=\frac{U_0}{\dot I(0\,{\rm s})}\). Mit dem Wert aus der Anpassung ergibt sich dann: \(L=\frac{U_0}{\dot I(0\,{\rm s})}=\frac{\rm 12\,V}{\rm 904\,A/s}=13\,{\rm mH}\)
Hinweis: Alternativ kann man auch zeichnerisch die Steigung der Tangenten bestimmen.
c) Durch die Permeabilitätszahl des Eisens erhöht sich die Induktivität der Spule. Ihr Widerstand bleibt gleich. Für die zeitliche Ableitung \(\dot I(t)\) der Stromstärke gilt \(\dot I(𝑡) = −\frac{𝑈_{\rm ind}(𝑡)}{𝐿}\). Bei gleicher Induktionsspannung ist die Steigung im \(I(t)\)-Diagramm immer kleiner, d. h., der Anstieg der Stromstärke verläuft flacher. Da sich der Widerstand nicht ändert, bleibt auch der Grenzwert \(𝐼_{\rm max}\), gegen den die Stromstärke strebt, gleich.
Aufgabe 3
a) Eine Induktionsschleife wirkt wie eine Spule. Der Zug wirkt wie ein Eisenkern und verändert die Induktivität der Spule. Das kann gemessen werden.
b) Für die Induktionsspannung gilt: \(U_{\rm i} = –L \cdot \dot I\). Wir setzen hier \(I(t) = I_{\rm max}\cdot \sin(\omega\cdot t)\) ein und erhalten so die obige Gleichung für die Induktionsspannung \(U_{\rm i} = –L \cdot \dot I=-L\cdot \omega\cdot I_{\rm max}\cdot \cos(\omega\cdot t)\).
c) Der Wechselstromwiderstand \(R(ω)\) ist der Quotient aus den Maxima der Spannung und Stromstärke. Wir setzen die obigen Terme ein: \(R(ω) = L \cdot ω \cdot \frac{I_{\rm max}}{I_{\rm max}} = L \cdot ω\).
d) Im Modellversuch schließen wir an die Leiterschleife eine Wechselspannung an, messen die Effektivwerte dieser Spannung und Stromstärke und bilden den Quotienten: \(\frac{U_{\rm eff}}{I_{\rm eff}}=\frac{U_{\rm max}}{I_{\rm max}}=R(\omega)\)
Dann lassen wir eine Spielzeuglokomotive auf die Leiterschleife fahren und messen den veränderten Wechselstromwiderstand.
Aufgabe 4
a) Für die Induktionsspannung einer Leiterschleife gilt gemäß dem Induktionsgesetz: \(U_i = –A \cdot \dot B\). Wir setzen den angegebenen Term für \(B\) ein. Mit \(A=\pi\cdot R^2\) folgt also:
\(U_i = –A \cdot \dot B=-\pi R^2\cdot \frac{\mu_0}{2R}\cdot \dot I=-\pi R^2\cdot \frac{\mu_0}{2R}\cdot \frac{\Delta I}{\Delta t}\)
b) Der resultierende Term für \(U_i\) muss gleich \(U_i = –L \cdot I\) sein, da beide Terme die gleiche Induktionsspannung beschreiben. Wir setzen die Terme gleich und nach \(L\) auf, so erhalten wir den angegebenen Term für \(L\). Wir setzen ein und berechnen:
\(L=N^2\cdot \mu_0\cdot\frac{\pi \cdot R}{2}=49,8\,{\rm µH}\)
c) Die Induktivität erhöht sich um den Faktor 10 auf \(L = 498\,{\rm μH}\). Dadurch erhöht sich auch \(R(ω) = L \cdot ω\) um den Faktor 10.
Transformator
Aufgabe 1
Durch den Wechselstrom ändert sich das Magnetfeld in der Spule ständig, sodass ein elektrisches Wirbelfeld induziert wird. Da Eisen ein elektrischer Leiter ist, gibt es dadurch auch elektrische Wirbelströme. Durch die Wärmewirkung des Stroms erwärmt sich der Eisenkern.
Aufgabe 2
a) Die Feldlinien des elektrischen Wirbelfelds verlaufen orthogonal zur Längsachse des Eisenkerns. Ein größerer Wirbelstrom wie bei einem massiven Eisenkern wird bei A durch die isolierenden Lacksichten unterbrochen, sodass es nur innerhalb der einzelnen Eisenschichten zu kleineren Wirbelströmen kommen und die Erwärmung deswegen kleiner ist. Bei B liegen die Lackschichten parallel zu den Feldlinien des elektrischen Wirbelfeldes und haben deswegen keinen Einfluss auf die Ausbildung der Wirbelströme.
b) Bei Transformatoren wird durch die Stromänderung in der Primärspule eine Spannung in der Sekundärspule induziert. Die Erwärmung des Eisenkerns zeigt, dass ein Teil der Energie dort in thermische Energie umgewandelt wird und nicht auf die Sekundärspule übertragen wird. Dies er unerwünschte Effekt wird durch geblätterte Eisenkerne wie in b) geschildert vermindert.
Aufgabe 3
a) Die Zuordnung ist: Feldspule (1), Induktionsspule (2), Energiezufuhr (3), Verbraucher (4), Lastwiderstand (4).
Im Eisenkern entsteht ein gemeinsamer magnetischer Fluss \(\phi(t)\) und eine gemeinsame Flussänderungsrate \(\phi(t)\). Dadurch kommt es in beiden Spulen zu Induktionsspannungen. Bei dieser Anwendung führt die Feldspule dem Eisenkern permanent magnetische Energie zu, während die Induktionsspule dem Eisenkern ständig magnetische Energie entzieht.
b) Wir lösen die Gleichung nach \(U_2\) auf: \(U_2=U_1\cdot\frac{N_2}{N_1}\)
Einsetzen liefert: \(U_2=5\,{\rm V}\)
c) Im Anwendungsfall vermeidet man Ohmsche Energieverluste, indem man den Transformator so auslegt, dass der Ohmsche Widerstand vernachlässigbar ist. Dadurch wird in der Feldspule entsprechend dem Induktionsgesetz die Stromstärke begrenzt durch die selbst induzierte Spannung \(U_{\rm ind}(t) = –N_1 \cdot \phi(t) = U_1(t)\). Somit liegt diese Spannung an der Feldspule an. Bei der Induktionsspule entsteht gemäß dem Induktionsgesetz die Induktionsspannung \(U_{\rm ind}(t) = –N_2 \cdot \phi(t) = U_2(t)\). Wir bilden den Quotienten: \(\frac{U_1(t)}{U_2(t)}=\frac{N_1(t)}{N_2(t)}\)
In diesem Idealfall gilt also die obige Gleichung. Es entsteht im Idealfall sogar keine Phasenverschiebung.
d) Wir lösen nach \(I_2\) auf: \(I_2=I_1\cdot\frac{U_1}{U_2}\)
Einsetzen liefert: \(I_2=I_1\cdot\frac{N_1}{N_2}=I_1\)
Die Leistung ist das Produkt aus Spannung und Stromstärke, \(P(t) = U(t) \cdot I(t)\). Wir wenden am Lastwiderstand das Ohmsche Gesetz an mit der Relation \(U(t) = R \cdot I(t)\). Damit gilt \(P(t) = R_L \cdot I(t)^2\).
Die Messwerte aus Abb. 5 zeigen: \(U(I) = 2,2\,{\rm V} –I\cdot\frac{2,2\,{\rm V}}{0,05\,{\rm A}} = 2,2 V – I \cdot 44\,{\rm \Omega}\). Wenn am Lastwiderstand das Ohmsche Gesetz gilt, dann gibt es keine Phasenverschiebungen zwischen der Spannung \(U(t)\) und der Stromstärke \(I(t)\). Dann können wir die Leistung \(P(t) = U(t) \cdot I(t)\) einfacher durch die mit einem Multimeter gemessenen Messwerte \(U\) und \(I\) ermitteln mit \(P = U \cdot I\). Dann können wir in diesen Term U(I) einsetzen: \(P(I) = U \cdot I = 2,2\,{\rm V} \cdot I – 44\,{\rm Ω} \cdot I^2\). Die Funktion \(P(I)\) stellt eine nach unten offene Parabel dar. Das entspricht Abb. 5b und es bestätigt somit die Gültigkeit des Ohmschen Gesetzes am Lastwiderstand.
e) Im Idealfall ist der Innenwiderstand der Spulen null und die von der ersten Spule zugeführte Leistung \(P_1 = U_1 \cdot I_1\) ist gleich der zur zweiten Spule übertragenen Leistung \(P_2 = U_2\cdot I_2\). Wir setzen die Leistungen daher gleich: \(U_1 \cdot I_1 = U_2 \cdot I_2\). Wir lösen nach \(I_1\) auf: \(I_1 = I_2\cdot\frac{U_2}{U_1}\).
Aufgabe 4
Beschreibung der Messwerte in Abb. 5: Bei einem Lastwiderstand von null ist die Stromstärke \(I\) maximal und die Leistung \(P_L\) null. Mit zunehmendem Lastwiderstand \(R_L\) nimmt \(I\) ab und \(U_L\) zu. Die Leistung \(P_L\) nimmt zunächst zu, erreicht ein Maximum und nimmt dann wieder ab. Die Messwerte in Abb. 5 zeigen: Das Maximum der Leistung tritt beim Lastwiderstand \(R_L = 47\,{\rm Ω}\) auf.
© Cornelsen Verlag GmbH, Berlin