Hinweise:
Nimm für Aufgabe 2c) zu Teilchen im elektrischen Feld einen Kondensator mit gleicher Länge \(l\) und Breite \(b\) an.
Nimm für Aufgabe 1b) zu Leiter im Magnetfeld eine Stromstärke von \(10\,{\rm A}\) und eine Leiterlänge von \(20\,{\rm cm}\) an.
Nimm bei Aufgabe 3 zu Beschleunigung von Protonen im Zyklotron die gleiche magnetische Flussdichte wie für Aufgabe 2 an, also \(B=0,51\,{\rm T}\).
Teilchen im elektrischen Feld
Aufgabe 1
Die Geschwindigkeit ergibt sich über \(v=\sqrt{\frac{2\cdot q\cdot U_1}{m}}\).
Ein Elektron hat die Masse \(m_e=9,11\cdot 10^{-31}\,{\rm kg}\) und Ladung \(-1e\), somit: \(v=10,3\cdot 10^{6}\,\frac{\rm m}{\rm s}\)
Ein Proton hat die Masse \(m_p=1,67\cdot 10^{-27}\,{\rm kg}\) und die Ladung \(1e\), somit: \(v=239,7\,\frac{\rm km}{\rm s}\)
Ein Alpha-Teilchen hat die Masse \(m_\alpha=4\,{\rm u}=6,64\cdot 10^{-27}\,{\rm kg}\) und die Ladung \(2e\) und somit \(v=170,1\,\frac{\rm km}{\rm s}\)
Aufgabe 2
a) Die Größte Teilchengeschwindigkeit ist die des Elektrons und beträgt nur 3,4 % der Lichtgeschwindigkeit. Deshalb ist eine relativistische Rechnung nicht notwendig.
b) Das Elektron ist negativ geladen und wird zur positiven Platte hin abgelenkt. Das Proton und das Alpha-Teilchen werden von der negativen Platte angezogen.
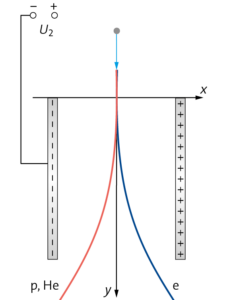
c) Nimm hier einen quadratischen Kondensator mit \(l=d\) an.
Die maximale Ablenkspannung \(U_2\) ist diejenige Spannung, bei der die Ablenkung so groß ist, dass die Teilchen die Kondensatorplatten treffen würden, bevor sie den Kondensator verlassen.
Für die horizontale Ablenkung \(x\) im Kondensator durch \(U_2\) , abhängig von der vertikalen Strecke \(y\), gilt:
\(x=\frac{q\cdot U}{2\cdot m\cdot d}\cdot\left(\frac{y}{v}\right)^2=\frac{q\cdot U}{2\cdot m\cdot d\cdot v^2}\cdot y^2\)
Für die Geschwindigkeit kann man die Geschwindigkeit aus Aufgabe 1 verwenden: \(v=\sqrt{\frac{2\cdot q\cdot U_1}{m}}\) Einsetzen und kürzen ergibt folgende Gleichung:
\(x=\frac{1}{4\cdot d}\cdot\frac{U_2}{U_1}\cdot y^2\)
Die Ablenkung ist also für alle geladenen Teilchen gleich. Wir nehmen an, dass die Kondensatorplatten die Länge \(l\) haben und \(l=3\,{\rm cm}\) lang sind. Dann ergibt sich mit der maximal möglichen Ablenkung \(x_{\rm max}=\frac{d}{2}=1,5\,{\rm cm}\) eine Formel für die maximale Spannung:
\(U_{\rm 2,max}=\frac{4\cdot U_1\cdot d}{l^2}\cdot x_{\rm max}=600\,{\rm V}\)
d) Da auf die Teilchen nach dem Verlassen des Kondensators keine Kraft mehr wirkt, bewegen sie sich unbeschleunigt, also geradlinig gleichförmig weiter, Ihre Bahnkurve ist dann eine gerade Linie.
e) Das Proton und die anderen Teilchen bewegen sich auf einer Geraden. Da hier die Ablenkung horizontal erfolgt, geben wir die Geradengleichung als \(x(y)=x_0+m\cdot x\) mit Achsenabschnitt \(x_0\) und Steigung \(m\) an. Denn die horizontale Ablenkung \(x\) hängt von der vertikal zurückgelegten Strecke \(y\) ab. Für den \(x\)-Achsenabschnitt gilt dann: \(x_0=\frac{l^2\cdot U_2}{4\cdot d\cdot U_1}\).
Die Steigung \(m\) ergibt sich aus der vorher berechneten Formel für die Ablenkung an der Stelle \(y=l\) zu: \(m=x(y=l)= \frac{l\cdot U_2}{2\cdot d\cdot U_1}\)
Damit erhält man die Geradengleichung: \(x(y)=\frac{l^2\cdot U_2}{4\cdot d\cdot U_1} + \frac{l\cdot U_2}{2\cdot d\cdot U_1}\cdot y=\frac{l\cdot U_2}{4\cdot d\cdot U_1}\cdot (l+2\cdot y)\)
Einsetzen der Werte \(U_1=300\,{\rm V}\), \(U_2=600\,{\rm V}\) und \(l=d=3\,{\rm cm}\) für \(y=5\,{\rm cm}\) ergibt \(x=6,5\,{\rm cm}\).
Aufgabe 3
a) Gleichsetzen von elektrischer Kraft \(F_{el}=q\cdot \frac{U}{d}\) und Gravitationskraft \(F_g=m\cdot g\) und Einsetzen von \(m=\rho\cdot V=\rho\cdot\frac{4}{3}\cdot\pi\cdot r^3\) ergibt:
\(q=\frac{4}{3}\cdot\pi\cdot\frac{\rho\cdot g\cdot d}{U}\cdot r^3\)
b)
| \(r\) in µm | 0,2 | 0,4 | 0,3 | 0,5 | 0,2 | 0,3 | 0,4 | 0,5 |
| \(U\) in V | 18,5 | 148,9 | 31,3 | 144,5 | 9,2 | 20,8 | 49,3 | 96,1 |
| \(q\) in \(10^{-19}\,{\rm C}\) | 1,60 | 1,59 | 3,19 | 3,20 | 3,22 | 4,79 | 4,80 | 4,81 |
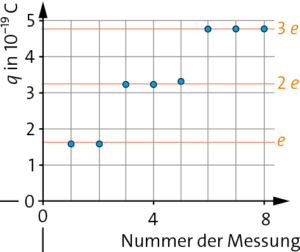
Die Elementarladung ist \(e=1,602\cdot 10^{-19}\,{\rm C}\). Die aus den Messwerten berechneten Ladungen entsprechen ca. der einfachen, doppelten und dreifachen Elementarladung. Es gibt keine Werte, die dazwischen liegen. Das Experiment deckt sich also mit den Erwartungen.
Bahnen von Ladungsträgern im Magnetfeld
Aufgabe 1
a) Gegeben: \(v=1,0\cdot 10^7\,\frac{\rm m}{\rm s}\); \(B=0,95\cdot 10^{-3}\,{\rm T}\); \(m_e=9,11\cdot 10^{-31}\,{\rm kg}\)
Gesucht ist die Beschleunigungsspannung \(U\). Diese kann man aus der Energiebilanz herleiten: \(E_{el}=q\cdot U=\frac{m}{2}\cdot v^2=E_{\rm kin}\Rightarrow U=\frac{m_e\cdot v^2}{2\cdot e}=285\,{\rm V}\)
b) Im homogenen Magnetfeld wirkt die Lorentzkraft orthogonal zur Flussdichte \(\vec{B}\) und zur Geschwindigkeit\(\vec{v}\). Dadurch ändert sich die Richtung der Geschwindigkeit, ihr Betrag bleibt konstant. Die Lorentzkraft steht dabei immer orthogonal zur Bewegungsrichtung. Sie bringt die für die Kreisbewegung notwendige Zentripetalkraft auf.
c) Aus \(F_L=F_Z\) folgt: \(r=\frac{m_e\cdot v}{e\cdot B}=0,06\,{\rm m}=6\,{\rm cm}\)
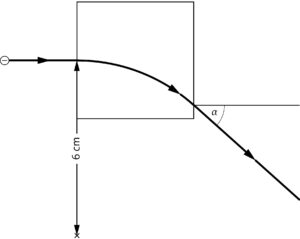
d) Die Elektronen treten unter einem Winkel \(\alpha = 42°\) zur Horizontalen aus dem Magnetfeld aus. Nach dem Verlassen des Magnetfelds bewegen sich die Elektronen ab dem Austrittspunkt geradlinig auf einer Tangente zur Kreisbahn.
Aufgabe 2
a) Die Lorentzkraft bringt die für die Kreisbewegung notwendige Zentripetalkraft auf. Es gilt: \(F_L=F_Z\Rightarrow r=\frac{m\cdot v}{q\cdot B}\)
b) Der Bahnradius ist proportional zur Geschwindigkeit und zur Masse der Ladungsträger. Er ist antiproportional zur Ladung und zur Flussdichte \(B\). Das heißt, je größer die Geschwindigkeit oder die Masse der Ladungsträger ist, desto größer ist der Radius . Je größer die Ladung oder die Flussdichte ist, desto kleiner ist der Radius.
c) Man stellt die Formeln für den Radius für die verschiedenen Ladungsträger mithilfe der atomaren Masseneinheit u und der Elementarladung \(e\) auf und vergleicht sie miteinander:
Protonen \((m_p=1\text{u},\ q=e)\): \(r_p=\frac{1\cdot \text{u}\cdot v}{e\cdot B}\)
\({\rm He^+}\)-Ionen \((m_{\rm He+}=4\text{u},\ q=e)\): \(r_{\rm He+}=\frac{4\cdot \text{u}\cdot v}{e\cdot B}\)
\({\rm He^{2+}}\)-Ionen \((m_{\rm He2+}=4\text{u},\ q=2e)\): \(r_{\rm He2+}=\frac{4\cdot \text{u}\cdot v}{2\cdot e\cdot B}=\frac{1\cdot \text{u}\cdot v}{e\cdot B}\)
Somit gilt \(r_{\rm He+}>r_{\rm He2+}>r_p\). Die Bahn der He+-Ionen hat den größten Radius. Der Bahnradius der He2+-Ionen ist nur halb so groß. Die Bahn der Protonen hat den kleinsten Radius.
Aufgabe 3
a) Die Teilchen bewegen sich senkrecht zu den Magnetfeldlinien. Damit wirkt die Lorentzkraft senkrecht auf die Teilchenbahn und senkrecht zum Magnetfeld. Deshalb bewegen sich die Teilchen auf Kreisbahnen mit konstantem Radius. Die Drehrichtung ergibt sich aus der Richtung der Lorentzkraft über die Drei-Finger-Regel. Alle Ionen sind positiv geladen, das Magnetfeld zeigt aus der Zeichenebene heraus, die Bewegung erfolgt deshalb im Uhrzeigersinn.
b) Der Radius für \({\rm Ne^{+}}\) ergibt sich über \(F_L=F_Z\) zu: \(r_{\rm Ne+}=\frac{m\cdot v}{q\cdot B}=0,06\,{\rm m}=6\,{\rm cm}\)
Für \({\rm Ne^{2+}}\) ergibt sich wegen der doppelten Ladung und gleichen Masse der halbe Radius, also eine engere Bahn mit \(r_{\rm Ne2+}=3\,{\rm cm}\). Das \({\rm Ar^{2+}}\)-Ion hat die doppelte Masse und die doppelte Ladung wie \({\rm Ne^{+}}\) und damit den gleichen Radius: \(r_{\rm Ar2+}=6\,{\rm cm}\)
\({\rm Ar^{+}}\) hat die doppelte Masse, aber die gleiche Ladung und damit den doppelten Radius: \(r_{\rm Ne+}=12\,{\rm cm}\)
c) Bahn C gehört zum \({\rm Ne^{2+}}\)-Ion, da es den kleinsten Radius besitzt. Bahn A gehört zu den Ionen \({\rm Ne^{+}}\) und \({\rm Ar^{2+}}\), die den gleichen Radius haben. Bahn B gehört zum \({\rm Ar^{+}}\)-Ion, das mit der kleinsten Ladung und größten Masse die Bahn mit dem größten Radius beschreibt.
Leiter im Magnetfeld
Aufgabe 1
Hinweis: Nimm für Teilaufgabe b) eine Stromstärke von \(10\,{\rm A}\) und eine Leiterlänge von \(20\,{\rm cm}\) an.
a) Leiter waagerecht (parallel zu den Beinen des Magneten) mit Minuspol links und Pluspol rechts: Die Lorentzkraft auf die linke und rechte Seite des Leiters zeigt nach außen und hebt sich auf. Es bleibt die Kraft auf die Stirn des Leiters, die (nach der Drei-Finger-Regel) den Leiter in den Magneten zieht. Befindet sich die Stirn des Leiters aber außerhalb des Magnetfeldes, wirkt keine Kraft.
Umgekehrte waagerechte Position: Es wirkt keine Kraft bzw. der Leiter wird aus dem Magnetfeld herausgedrückt.
Leiter senkrecht zum Magnetfeld (Minuspol oben und Pluspol unten): Auf den oberen Teil des Leiters wirkt die Lorentzkraft entsprechend der Drei-Finger-Regel nach links. Auf den unteren Teil wirkt sie nach rechts. Der Leiter wird zu einer Drehung entgegen dem Uhrzeigersinn gezwungen.
Umgekehrte senkrechte Position: umgekehrte Kraftrichtung.
b) Mit \(10\,{\rm A}\) und \(20\,{\rm cm}\) folgt: \(B=\frac{F}{I\cdot l}=\frac{\rm 23,1\,mN}{I\cdot l}=11,5\,{\rm mT}\)
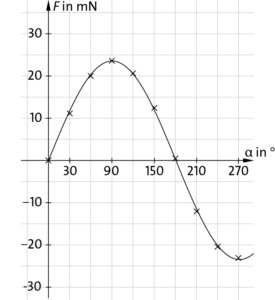
c) Das Vorzeichen wechselt, weil sich die Kraftrichtung umkehrt. Aus dem Verlauf des Graphen kann man ableiten, dass folgender Zusammenhang gilt: \(F\sim \sin(\alpha)\)
Aufgabe 2
a)
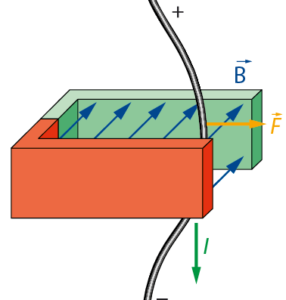
Als Beispiel ist ein stromführender Draht im homogenen Feld eines Hufeisenmagneten geeignet. Man ordnet den Draht so an, dass er orthogonal zur Flussdichte steht (Skizze). Mit der Drei-Finger-Regel der rechten Hand kann man dann die Richtung der Kraft angeben. Wenn der Strom von oben nach unten gerichtet ist, dann zeigt die Kraft nach rechts. Wird die Stromrichtung umgepolt, dann zeigt die Kraft nach links. Wenn man den Hufeisenmagnet um 180° dreht, dann wird der Leiter bei gleicher Stromrichtung wieder nach rechts abgelenkt.
b)
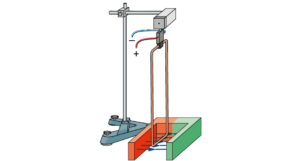
Aufgabe 3
a) Mit zunehmender Stromstärke steigt auch die Kraft auf den Draht. An den Messwerten kann man erkennen, dass sich die Kraft bei doppelter (dreifacher, fünffacher) Stromstärke verdoppelt (verdreifacht, verfünffacht). Auch bei den Messwerten verschiedener Drahtlängen ist eine Proportionalität zu erkennen: Bei doppelter (vierfacher) Drahtlänge verdoppelt (vervierfacht) sich die Kraft. Damit muss die Kraft auch proportional zum Produkt \(I\cdot s\) sein. Das überprüft man für alle Messdaten, indem man für jedes Wertepaar den Quotienten \(\frac{F}{I\cdot s}\) berechnet: Man sieht, dass der Quotient im
Rahmen der Messgenauigkeit konstant ist. Folglich ist \(F\sim I\cdot s\)
Variation der Stromstärke, \(s=5,0\,{\rm cm}\):
| \(I\) in A | 0,50 | 0,80 | 1,60 | 2,50 | 4,80 |
| \(F\) in mN | 0,7 | 1,1 | 2,3 | 3,5 | 6,7 |
| \(\frac{F}{I\cdot s}\) in \(\frac{\rm mN}{\rm A\cdot m}\) | 28,0 | 27,5 | 28,8 | 28,0 | 27,9 |
Variation der Drahtlänge, \(I=2,0\,{\rm A}\):
| \(s\) in cm | 2,0 | 4,0 | 5,0 | 8,0 | 10,0 |
| \(F\) in mN | 1,1 | 2,3 | 2,8 | 4,5 | 5,6 |
| \(\frac{F}{I\cdot s}\) in \(\frac{\rm mN}{\rm A\cdot m}\) | 27,5 | 28,8 | 28,0 | 28,1 | 28,0 |
b) Unter Berücksichtigung aller Messwerte erhält man als Mittelwert für den Quotienten \(\frac{F}{I\cdot s}=28\,{\rm mT}\). Dieser Quotient entspricht der magnetischen Flussdichte \(B\) des homogenen Felds.
Geschwindigkeitsfilter und Massenspektrometer
Aufgabe 1
a) Beim Wienschen Filter stehen ein elektrisches Feld der Feldstärke \(\vec{E}\)und ein Magnetfeld der Flussdichte \(\vec{B}\) orthogonal zueinander. Wenn ein Proton orthogonal zu den gekreuzten Feldern in den Filter eintritt, dann wirken die elektrische Kraft und die Lorentzkraft in entgegengesetzter Richtung auf das Proton. Nur wenn zwischen diesen Kräften ein Kräftegleichgewicht herrscht, können die Protonen den Filter geradlinig passieren. Das ist nur für eine bestimmte Geschwindigkeit der Fall. Protonen mit größerer oder kleinerer Geschwindigkeit werden nach oben bzw. nach unten abgelenkt und gelangen nicht durch die Öffnung am Ende des Filters. Der Filter ist also ein Geschwindigkeitsfilter.
b) Damit ein Proton den Filter geradlinig passieren kann, muss ein Kräftegleichgewicht zwischen der elektrischen Kraft \(F_{el}\) und der Lorentzkraft \(F_L\) herrschen:
\(F_{el}=F_L\rightarrow e\cdot E=e\cdot v\cdot B\Rightarrow v=\frac{E}{B}\)
c) Gegeben: \(U=750\,{\rm V}\); \(d=0,02\,{\rm m}\); \(v=5,2\cdot 10^4\,\frac{\rm m}{\rm s}\)
Für die Geschwindigkeit der Protonen, die den Filter passieren können, gilt: \(v=\frac{E}{B}\Rightarrow B=\frac{E}{v}\)
Mit \(E=\frac{U}{d}=37\,500\,\frac{\rm V}{\rm m}\) folgt: \(B=0,72\,\frac{\rm V\cdot s}{\rm m^2}=0,72\,{\rm T}\)
d) Für die Geschwindigkeit der Protonen gilt \(v=\frac{U}{d\cdot B}\). Wenn man die Flussdichte und die Spannung halbiert, dann bleibt die Geschwindigkeit gleich. Felix’ Aussage trifft nicht zu. Wenn man nur die Spannung halbiert, dann wird die Geschwindigkeit halbiert. Deniz’ Aussage trifft zu. Wenn man die Flussdichte oder den Plattenabstand verdoppelt, dann wird die Geschwindigkeit halbiert. Die Aussagen von Marit und Taira treffen ebenfalls zu.
Aufgabe 2
a) Von der Elektronenstrahlablenkung im orthogonalen homogenen elektrischen Feld zwischen zwei geladenen Kondensatorplatten weiß man, dass die Ablenkung umso kleiner ist, je größer die Geschwindigkeit der Elektronen ist. Dementsprechend weisen die Ionen höherer Geschwindigkeit im elektrischen Feld eine geringere Bahnkrümmung auf und es gilt: \(v_1 > v_2\). Im Magnetfeld werden die Ionen gleicher Geschwindigkeit unterschiedlich stark abgelenkt, da der Bahnradius proportional zur Masse ist. Die Ionen größerer Masse werden weniger stark abgelenkt. Diese Ladungsträger wurden auch im elektrischen Feld weniger stark abgelenkt. Demnach spielt auch im elektrischen Feld die Masse eine Rolle. Hinweis: Im elektrischen Feld ist die Ablenkung umso kleiner, je größer die kinetische Energie der Ionen ist. Im Magnetfeld ist der Krümmungsradius umso größer, je größer der Impuls der Ionen ist.
b) Da der Radius der Bahn im Magnetfeld proportional zur Masse ist, treffen die Ladungsträger kleinerer Masse in Punkt ① und diejenigen größerer Masse in Punkt ② auf den Detektor.
Fadenstrahlrohr
Aufgabe 1
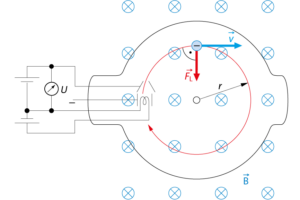
Bei einem Fadenstrahlrohr werden von einer Glühkathode kommende Elektronen in einem Vakuumkolben beschleunigt. Die Beschleunigung geschieht senkrecht zu den Feldlinien eines homogenen Magnetfeldes. Deshalb wirkt die Lorentzkraft \(F_L=q\cdot v\cdot B\) auf die Elektronen und diese werden auf einer Kreisbahn gelenkt. Da die Elektronen überall gleich schnell sind und sich immer senkrecht zum Magnetfeld bewegen, ist der Radius konstant. Der Radius hängt von der Masse und der Ladung der Elektronen ab, es gilt: \(\frac{e}{m}=\frac{v}{r\cdot B}\). Für \(m_e\) ist dies die spezifische Ladung des Elektrons. Durch Messung von Geschwindigkeit, Radius und magnetsicher Flussdichte kann man diese bestimmen.
Aufgabe 2
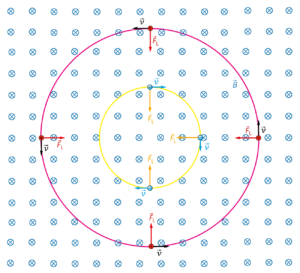
Wir nehmen an, dass ein Proton mit der gleichen Geschwindigkeit in das Fadenstrahlrohr eintreten würde. Die Bahn des Protons startet in entgegengesetzter Richtung, da es nicht in Richtung des Minus- sondern des Pluspols beschleunigt wird. Es kehrt sich auch die Richtung der Lorentzkraft um, weshalb das Proton eine umgekehrte Drehrichtung besitzt. Bewegt sich das Elektron im Uhrzeigersinn, bewegt sich das Proton entgegen des Uhrzeigersinns. Außerdem ist der Radius der Kreisbahn für das Proton wegen \(r\sim m\) größer, da die Masse größer ist. Achtung: In der Skizze ist das Verhältnis der Bahnkurven nicht maßstabsgetreu. Da die Masse des Protons mit \(\frac{m_p}{m_e}\approx 1836\) deutlich größer ist als die des Elektrons, ist die Kreisbahn des Protons um einen Faktor 1836 größer.
Aufgabe 3
Wie bei der Funktionsweise in Aufgabe 1 beschrieben, gilt \(F_L=F_Z\) und damit \(\frac{m\cdot v^2}{r}=q\cdot v\cdot B\). Durch Umformung folgt \(\frac{q}{m}=\frac{v}{r\cdot B}\) und für die Größen des Elektrons: \(\frac{e}{m_e}=\frac{v}{r\cdot B}\)
Aufgabe 4
a)
| \(B\) in T | 0,00381 | 0,00248 | 0,00189 | 0,00151 |
| \(r\) in m | 0,04 | 0,06 | 0,08 | 0,10 |
| \(\frac{1}{B^2}\) in \(\frac{1}{\rm T^2}\) | 68 889 | 162 591 | 279 947 | 438 577 |
| \(r^2\) in \({\rm m^2}\) | 0,0016 | 0,0036 | 0,0064 | 0,0100 |
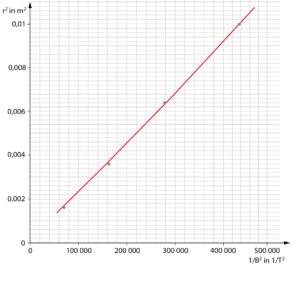
b) Hinweis: Mit der angegebenen Spannung von \(125\,{\rm V}\) ergibt sich ein etwa 10-mal kleinerer Wert für die spezifische Ladung. Nimm hier für die Berechnung eine korrigierte Spannung von \(2,06\,{\rm kV}\) an.
Es gilt der Zusammenhang \(r^2=2\cdot U\cdot \frac{e}{m}\cdot\frac{1}{B^2}=k\cdot\frac{1}{B^2}\). Deshalb kann man die Geradensteigung \(k\) über ein Steigungsdreieck aus dem Diagramm abschätzen:
\(k=\frac{\Delta r^2}{\Delta\left(\frac{1}{B^2}\right)}=\frac{0,010\,{\rm m^2}-0,0036\,{\rm m^2}}{439\,000\,{\rm T^{-2}}-165\,000\,{\rm T^{-2}}} \approx 2,34\cdot 10^{-8}\,\,{\rm m^2\cdot T^2}\)
Es folgt die spezifische Ladung über \(\frac{e}{m_e}=\frac{2\cdot U}{k}=1,76\cdot 10^{11}\,\frac{\rm C}{\rm kg}\). Verglichen mit der spezifischen Ladung des Elektrons von \(1,73\cdot 10^{11}\,\frac{\rm C}{\rm kg}\) muss es sich hier also um ein Teilchen mit einer etwa zehnfachen Ladung handeln.
c) Für ein Proton ist die Gerade im Vergleich zu einem Elektron durch seine größere Masse steiler. Die Messwerte für \(r\) wären um den Faktor \(\frac{m_p}{m_e}\approx 1836\) größer.
Beschleunigung von Protonen im Zyklotron
Aufgabe 1
Im elektrischen Feld zwischen den Duanten bewegen sich die Protonen parallel zu den elektrischen Feldlinien. Die elektrische Feldkraft wirkt in Bewegungsrichtung, sodass die Protonen in Bewegungsrichtung beschleunigt werden. Die Richtung bleibt gleich, der Betrag der Geschwindigkeit nimmt zu. Innerhalb der Duanten bewegen sich die Protonen orthogonal zum Magnetfeld. Es wirkt nur die Lorentzkraft auf die Protonen, sodass sie auf eine Halbkreisbahn abgelenkt werden, auf der sie sich bis zum Spalt bewegen. Der Betrag der Geschwindigkeit bleibt konstant, es ändert sich nur die Richtung.
Aufgabe 2
a) Man kann die Spannung mit der Formel für die Geschwindigkeit \(v=\sqrt{\frac{2\cdot q\cdot U}{m}}\) bestimmen, indem man beide Seiten quadriert und nach \(U\) umstellt:
\(U=\frac{v^2\cdot m_p}{2\cdot e}=5\,012\,{\rm V}\approx 5\,{\rm kV}\)
b) Zwischen den Duanten muss eine Spannung von nahezu 10 kV anliegen, da in a) nur die halbe Strecke zwischen den Duanten zurückgelegt wurde.
c) Man setzt die gegebenen Werte in die Formel für den Radius ein:
\(r_1=\frac{m_p\cdot v_1}{e\cdot B}=0,02\,{\rm m}=2\,{\rm cm}\)
\(v_2=\sqrt{v_1^2+\frac{2\cdot e\cdot U}{m_p}}=1,696\cdot 10^6\,\frac{\rm m}{\rm s}\)
Aufgabe 3
Hinweis: Nimm hier die gleiche magnetische Flussdichte wie für Aufgabe 2 an, also \(B=0,51\,{\rm T}\).
Für die Umlaufdauer \(T\) bei einer Kreisbewegung mit dem Radius \(r\) und der Geschwindigkeit \(v\) gilt: \(T=\frac{2\cdot \pi\cdot r}{v}\)
Die gegebene Formel ist allerdings unabhängig vom Radius und der Geschwindigkeit. Sie hängt nur von der Ladung, der Masse und der Flussdichte ab. Um \(\frac{r}{v}\) zu ersetzen, geht man vom Zusammenhang aus, dass die Lorentzkraft als Zentripetalkraft wirkt:
\(F_L=F_Z\rightarrow e\cdot v\cdot B=\frac{m_p\cdot v^2}{r}\)
Umstellen nach \(\frac{r}{v}\) ergibt \(\frac{r}{v}=\frac{m_p}{e\cdot B}\). Einsetzen ergibt die gesuchte Formel: \(T=\frac{2\cdot \pi\cdot m_p}{e\cdot B}\)
Für das Magnetfeld aus Aufgabe 2 mit \(B=0,51\,{\rm T}\)gilt beispielsweise: \(T=1,29\cdot 10^{-7}\,{\rm s}\)
Aufgabe 4
a) \(F_L=F_Z\Rightarrow v=\frac{e\cdot B\cdot r}{m_p}=39\cdot 10^6\,\frac{\rm m}{s}\)
b) \(E_{\rm kin}=\frac{m_p}{2}\cdot v^2=1,28\cdot 10^{-12}\,{\rm J}=8\,{\rm MeV}\)
Hinweis: Da die Geschwindigkeit nur wenig größer als das 0,1-Fache der Lichtgeschwindigkeit ist, wird hier der nichtrelativistische Fall angenommen. Im relativistischen Fall erhält man 8,0775 MeV.
c) Bei jedem Umlauf im Zyklotron passieren die Protonen zweimal die Beschleunigungsstrecke und werden jeweils mit \(U = 10\,{\rm kV}\) beschleunigt. Pro Umlauf wird ihnen dabei die Energie \(\Delta E = 2 \cdot e \cdot 10\,{\rm kV} = 20\,{\rm keV}\) zugeführt. Für die gesamte Anzahl \(N\) der Umläufe gilt dann:
\(N=\frac{E_{\rm kin}}{\Delta E}=400\)
d) Bei einer größeren Spannung zwischen den Duanten werden die Protonen jeweils stärker beschleunigt und die Geschwindigkeit nimmt stärker zu. Die Bahnen haben jeweils einen größeren Radius. Der maximale Radius und damit die maximale Geschwindigkeit würde früher, also nach weniger Umläufen, erreicht.
e) Die erreichbare Geschwindigkeit \(v=\frac{e\cdot B\cdot r}{m_p}\) und damit die Austrittsenergie ist durch den im Aufbau maximal möglichen Bahnradius begrenzt. Man muss deshalb die Flussdichte erhöhen, damit mit dem gleichen Aufbau eine höhere Geschwindigkeit erreicht werden kann. Oder man muss ein Zyklotron mit einem größeren Radius verwenden.
Spule im Magnetfeld
Aufgabe 1
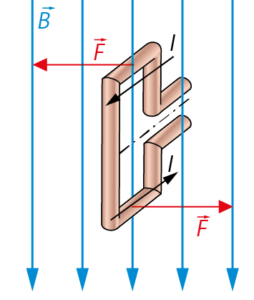
Auf die Teile, die parallel zu den Feldlinien liegen, wirkt keine Kraft, da \(I\) und \(B\) parallel zueinander sind. Eine Kraft wirkt auf die Teile der Spule, bei denen die Wicklungen senkrecht zum Magnetfeld verlaufen. Das ist oben und unten der Fall. Die Richtung der Stromstärke ist allerdings oben und unten entgegengesetzt, damit auch die wirkenden Kräfte. Vereinfacht lässt sich das für eine Leiterschleife so darstellen: \(F=l\cdot I\cdot B=3,1\,{\rm N}\)
Aufgabe 2
Es wirkt nur noch eine Kraft auf den unteren Teil der Spule. Die Kräfte bewirken eine Verschiebung der Spule in Längsrichtung.
Aufgabe 3
Wenn sich die Spule außerhalb des Magnetfeldes befindet, wirkt keine Kraft.
Hall-Effekt
Aufgabe 1
a) Bei positiven und negativen Ladungsträgern ist die Hall-Spannung umgekehrt.
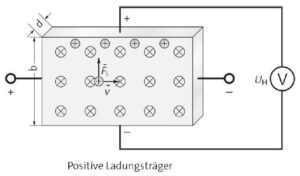
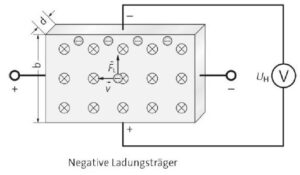
b) In einem stromführenden Halbleiterplättchen, das orthogonal zur Flussdichte \(\vec{B}\) steht, werden die bewegten Ladungen durch die Lorentzkraft verschoben, sodass sich zwischen der Ober- und Unterseite des Plättchens der Breite \(b\) ein elektrisches Feld aufbaut, bis sich ein Kräftegleichgewicht zwischen der elektrischen Feldkraft und der Lorentzkraft eingestellt hat. Es gilt: \(F_{el}=F_L\rightarrow e\cdot E=e\cdot v\cdot B\)
Mit der elektrischen Feldstärke \(E=\frac{U_H}{b}\) folgt: \(U_H=b\cdot v\cdot B\)
Aufgabe 2
a) Die Hall-Spannung ist proportional zur Stromstärke und zur Flussdichte. Je größer die Stromstärke oder die Flussdichte ist, desto höher ist die Hall-Spannung. Weiterhin ist die Hall-Spannung umgekehrt proportional zur Dicke des Plättchens. Je dicker es ist, desto geringer ist die Hall-Spannung. Um möglichst große Hall-Spannungen zu messen, sollte das Plättchen möglichst dünn sein und ein Material ausgewählt werden, das eine große Hall-Konstante hat. Außerdem ist die Hall-Spannung bei großer Flussdichte besonders groß.
b) \(U_H=R_H\cdot\frac{I\cdot B}{d}\Rightarrow R_H=\frac{U_H\cdot d}{I\cdot B}=2,38\cdot 10^{-4}\,\frac{\rm m^3}{C}\)
Das Plättchen besteht also aus Indiumantimonid.
Aufgabe 3
a) Man setzt die gegebene Formel für die Stromstärke in die Gleichung für die Hall-Spannung ein und stellt nach \(R_H\) um:
\(U_H=R_H\cdot \frac{I\cdot B}{d}=R_H\cdot \frac{e\cdot v\cdot b\cdot d\cdot n\cdot B}{d}\)
Mit \(U_H=b\cdot v\cdot B\) folgt damit: \(R_H=\frac{b\cdot v\cdot B}{e\cdot v\cdot b\cdot n\cdot B}=\frac{1}{e\cdot n}\)
b) Wenn man die Hall-Konstante gemessen hat, kann man über die in a) hergeleitete Formel die Ladungsträgerdichte bestimmen:
\(R_H=\frac{1}{e\cdot n}\Rightarrow n=\frac{1}{e\cdot R_H}\)
Aufgabe 4
a) Durch die Bewegung der Ladungsträger senkrecht zu den Feldlinien des Magnetfeldes wirkt die Lorentzkraft auf die Teilchen. Diese lenkt sie von ihrer Bahn ab und verursacht somit eine Ladungstrennung, bis es zu einem Kräftegleichgewicht von Lorentzkraft und elektrischer Kraft kommt: \(F_{el}=F_L\) Diese Ladungstrennung ist als elektrische Spannung \(U\) messbar.
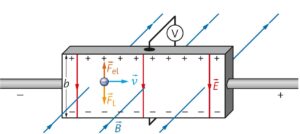
b) Der Effekt ist der Hall-Effekt. Durch das äußere Magnetfeld entsteht eine Spannung \(U\), die wir Hall-Spannung nennen. Sie ergibt sich durch Gleichsetzen der Ausdrücke für Lorentzkraft \(F_L=q\cdot v\cdot B\) und elektrische Kraft \(F_{el}=q\cdot\frac{U}{b}\):
\(U=v\cdot b\cdot B\)
© Cornelsen Verlag GmbH, Berlin