Elektrisches Feld
Aufgabe 1
Gegeben: \(𝑚 = 2,3 \cdot 10^{−6}\,{\rm kg}\); \(𝑞 = 0,11\cdot 10^{−9}\,{\rm C}\); \(E=|\vec{E}| = 15 \cdot 103 \, \frac{{\rm N}}{\rm C}\)
Kraft im elektrischen Feld: \(𝐹_{el} = 𝑞\cdot E= 0,11\cdot 10^{−9}\,{\rm C}\cdot 15\cdot 103\,\frac{\rm N}{\rm C}= 1,7\cdot 10^{−6}\,{\rm N} = 1,7 \,{µ\text{N}}\)
Gewichtskraft: \(𝐹_g = 𝑚\cdot 𝑔= 2,3\cdot 10{−6}\,{\rm kg}\cdot 9,8\,\frac{\rm N}{\rm kg}= 2,3\cdot 10{−5}\,{\rm N} = 23\,{\rm µN}\)
Die Gewichtskraft ist etwa eine Größenordnung größer als die elektrische Kraft.
Aufgabe 2
a) Diagramm mit Ausgleichsgerade durch den Punkt (0|0):
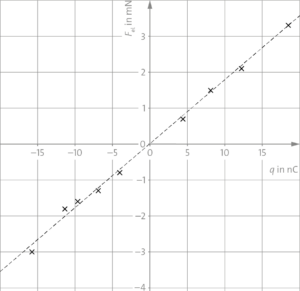
Feldstärke aus der Steigung der Ausgleichsgeraden:
\(|\vec{E}| =\frac{\Delta F_{el}}{\Delta q}=\frac{3,6\cdot 10^{−3}\,{\rm N}}{20\cdot 10^{−9}\,{\rm C}}=180\,000\frac{\rm N}{\rm C}=180\,\frac{\rm kN}{\rm C}\)
b) Berechnete Werte der Feldstärke:
| \(q\) in C | 4,5 | 8,2 | 12,3 | 18,6 | |
| \(F_{el}\) in mN | 0,7 | 1,5 | 2,1 | 3,3 | |
| \(E\) in \(\frac{\rm kN}{\rm C}\) | 156 | 183 | 171 | 177 | |
| \(q\) in C | -3,9 | -6,8 | -9,5 | -11,2 | -15,6 |
| \(F_{el}\) in mN | -0,8 | -1,3 | -1,6 | -1,8 | -3,0 |
| \(E\) in \(\frac{\rm kN}{\rm C}\) | 205 | 191 | 168 | 161 | 192 |
Mittelwert der Quotienten: \(E=178\,300\,\frac{\rm N}{\rm C}= 178,3\,\frac{\rm kN}{\rm C}\)
c) Die Methode der linearen Regression (z. B. mit einem Tabellenkalkulationsprogramm) ergibt: \(E=178\,000\,\frac{\rm N}{\rm C}= 178,0\,\frac{\rm kN}{\rm C}\)
d) Alle drei Methoden stimmen im Rahmen der Auswertegenauigkeit überein. Die grafische Methode hat den Nachteil, dass man die Ausgleichsgerade per Augenmaß einzeichnen muss und die Steigung nur ungenau ablesen kann. Sie zeigt aber sehr anschaulich die Streuung der Messwerte. Am genauesten ist, weil sie mathematisch begründet ist, die Methode der linearen Regression. Die Auswertung über den Mittelwert stimmt mit der Methode der linearen Regression sehr gut überein.
Aufgabe 3
Gegeben: \(q=12\cdot 10^{-9}\,{\rm C}\); Anzeige: 0,32 g
Die Anzeige der Waage in Gramm muss zuerst in eine Kraft umgerechnet werden. Da eine Waage normalerweise die Gewichtskraft misst und mithilfe des Ortsfaktors daraus die Masse bestimmt, muss man nun umgekehrt vorgehen:
\(F_{el}=m\cdot g=0,32\cdot 10^{-3}\,{\rm kg}\cdot 9,81\,\frac{\rm N}{\rm kg}=0,0031\,{\rm N}\)
Daraus folgt für die elektrische Feldstärke: \(E=\frac{F_{el}}{q}=\frac{3,1\cdot 10^{-3}\,{\rm N}}{12\cdot 10^{-9}\,{\rm C}}=260\,\frac{\rm kN}{\rm C}\)
Aufgabe 4
a) Nach dem Strahlensatz gilt \(\frac{F_{el}}{F_G}=\frac{x}{h}\). Für kleine Auslenkungen ist \(h\approx l\). Daraus folgt: \(\frac{F_{el}}{F_G}=\frac{x}{l}\)
b) Durch Umformen erhält man: \(F_{el}=\frac{x\cdot F_G}{l}=\frac{x\cdot m\cdot g}{l}\)
Damit folgt für die Feldstärke: \(E=\frac{F_{el}}{q}=\frac{x\cdot m\cdot g}{l\cdot q}=\frac{\rm 0,052\,m\cdot 0,45\cdot 10^{-3}\,kg\cdot 9,81\,\frac{N}{kg}}{\rm 1,2\,m\cdot 3,0\cdot10^{-9}\,C}=63\,\frac{\rm kN}{\rm C}\)
Feldlinien des elektrischen Feldes
Aufgabe 1
a)

b) Die Feldlinien zeigen von Plus nach Minus. Die resultierenden Feldlinien ergeben sich aus der Superposition der einzelnen Felder (vgl. Seite 36).

Aufgabe 2
a) Bild 1: Die Kraft auf einen gedachten positiv geladenen Probekörper zeigt von der linken Kugel weg bzw. zur rechten Kugel hin (in Feldlinienrichtung). Da die linke Kugel positiv geladen ist, muss die rechte Kugel negativ geladen sein. Aufgrund der Symmetrie des Feldlinienbilds ist ersichtlich, dass die Beträge der Ladungen \(Q_1\) und \(Q_2\) gleich sind. Also beträgt die Ladung der rechten Kugel \(Q_2= −1,0\,{\rm nC}\).
Bild 2: Wieder zeigt die Kraft auf einen positiv geladenen Probekörper von der linken Kugel weg bzw. zur rechten Kugel hin. Also muss die rechte Kugel erneut negativ geladen sein. Da nicht alle von der linken Kugel beginnenden Feldlinien auf der rechten Kugel enden, ist der Betrag der rechten Kugel kleiner als der der linken Kugel. Also ist \(Q_2=−0,5\,{\rm nC}\).
Bild 3: Die Kraft auf einen positiv geladenen Probekörper zeigt von beiden Kugeln weg, folglich müssen beide Kugeln positiv geladen sein. Das Feldlinienbild ist nicht symmetrisch; die Feldlinien der rechten Kugel verlaufen über die \(y\)-Achse nach links. Die von der linken Kugel auf einen Probekörper ausgeübte Kraft ist also größer als die Kraft von der rechten Kugel. Folglich ist der Betrag der Ladung der rechten Kugel größer als der der linken Kugel. Also ist\(Q_2=+2,0\,{\rm nC}\).
Bild 4: Wie bei Bild 3 müssen beide Kugeln positiv geladen sein. Da das Feldlinienbild symmetrisch ist, müssen auch die Beträge der Ladungen gleich sein. Also ist hier \(Q_2=+1,0\,{\rm nC}\).
b) Auf einen gedachten Probekörper werden Kräfte von beiden Kugeln ausgeübt. Da sich sowohl der Probekörper als auch die felderzeugenden Kugeln auf der \(x\)-Achse befinden, können die Kräfte aus Symmetriegründen nur in die \(x\)-Richtung oder entgegen zur x-Richtung zeigen. Folglich ist auch die auf den Probekörper wirkende resultierende Kraft parallel oder antiparallel zur x-Achse und damit wegen \(\vec{F}_{el}=q\cdot\vec{E}\) auch der Feldstärkevektor \(\vec{E}\).
c) Der Wert \(0\,\frac{\rm kN}{\rm C}\) gehört zum Bild 4, da hier auf einen Probekörper im Punkt (0|0) keine Kraft wirkt. Der Wert \(-3,6\,\frac{\rm kN}{\rm C}\) gehört zum Bild 3, da hier auf einen Probekörper im Punkt (0|0) eine Kraft nach links wirkt. Die beiden Werte \(5,4\,\frac{\rm kN}{\rm C}\) und \(7,2\,\frac{\rm kN}{\rm C}\) gehören zu den Bildern 1 und 2. Da in Bild 2 die Ladung der rechten Kugel kleiner ist, muss zum Bild 2 der kleinere Wert gehören, also \(5,4\,\frac{\rm kN}{\rm C}\). Zu Bild 1 gehört dann der größere Wert, also \(7,2\,\frac{\rm kN}{\rm C}\).
Aufgabe 3
a) Da durch jeden Punkt eines elektrischen Felds eine Feldlinie verläuft, gibt es streng genommen keine Feldliniendichte. In der Praxis zeichnet man aber immer nur eine Auswahl an Feldlinien. Die Dichte dieser gezeichneten Feldlinien, die z. B. von einem positiv geladenen Körper ausgehen, nimmt nach außen ab. Sie ist also ein qualitatives Maß für die Stärke des elektrischen Felds. Marc sollte also besser von der Dichte der gezeichneten Feldlinien sprechen.
b) Bei zwei positiv geladenen Kugeln gehen von jeder Kugel Feldlinien weg. Die Feldlinien verlaufen im Prinzip bis ins Unendliche. Entlang der Verbindungslinie der beiden Kugelmittelpunkte laufen die Feldlinien aufeinander zu. Dabei gibt es einen Punkt auf dieser Linie, auf dem die Kraft
auf einen Probekörper gleich null ist. In diesem Punkt gibt es kein elektrisches Feld. Feldlinien können also auch im Unendlichen oder in einem feldfreien Punkt enden.
Feld eines Plattenkondensators
Aufgabe 1
a) Gegeben: \(U=12\,000\,{\rm V}\); \(d=0,10\,{\rm m}\) Damit folgt: \(E=\frac{U}{d}=\frac{12\,000\,{\rm V}}{\rm 0,10\,m}=120\,\frac{\rm kV}{\rm m}\)
b) Gegeben: \(q=2,5\cdot10^{-9}\,\,{\rm C}\); \(m=0,40\cdot10^{-3}\,{\rm kg}\).
Damit folgt die Energie beim Aufprall: \(E_{\rm kin}=\Delta E=q\cdot U=2,5\dot 10^{-9}\,{\rm C}\cdot 12\,000\,{\rm V}=30\,\,{\rm µJ}\).
Geschwindigkeit beim Aufprall: \(v=\sqrt{\frac{2\cdot g\cdot U}{m}}=0,39\,\frac{\rm m}{\rm s}\)
c) Gegeben: \(U=6\,{\rm V}\); \(I=0,5\,{\rm A}\); \(\Delta t = 180\,{\rm s}\)
Leistung: \(P=U\cdot I=3\,{\rm W}\)
Geflossene Ladung: \(\Delta Q=I\cdot \Delta t=90\,{\rm C}\)
Übertragene Energie: \(\Delta E=U\cdot \Delta Q=6\,{\rm V}\cdot 90\,{\rm C}=540\,{\rm J}\) oder \(\Delta E=P\cdot \Delta t=540\,{\rm J}\)
Aufgabe 2
a und b)
| \(U\) in kV | 0 | 5 | 10 | 15 | 20 | 25 |
| \(F_{el}\) in mN | 0 | 0,75 | 1,6 | 2,2 | 3,0 | 3,8 |
| \(E\) in \(\frac{\rm kN}{\rm C}\) | 0 | 63 | 130 | 180 | 250 | 320 |
| \(\frac{U}{E}\) in \frac{\rm C\cdot V}{\rm N}\) | – | 0,080 | 0,077 | 0,083 | 0,080 | 0,078 |
c) Feldstärke und Spannung sind proportional zueinander, da der Quotient \(\frac{U}{E}\) im Rahmen der Messgenauigkeit konstant ist. Man könnte außerdem vermuten, dass der Quotient \(\frac{U}{E}\) gleich dem Plattenabstand ist.
Aufgabe 3
a und b)
| \(d\) in m | 0,05 | 0,10 | 0,15 | 0,20 | 0,25 |
| \(F_{el}\) in mN | 6,1 | 2,9 | 1,9 | 1,5 | 1,1 |
| \(E\) in \(\frac{\rm kN}{\rm C}\) | 510 | 240 | 160 | 130 | 92 |
| \(E\cdot d\) in \frac{\rm N\cdot m}{\rm C}\) | 26 | 24 | 24 | 26 | 23 |
c) Feldstärke und Plattenabstand sind umgekehrt proportional zueinander, da das Produkt \(E\cdot d\) im Rahmen der Messgenauigkeit konstant ist. Man könnte außerdem vermuten, dass das Produkt \(E\cdot d\) gleich der Spannung ist.
Aufgabe 4
a) Wir kürzen die Schreibweise für die Feldstärke wie gewohnt mit \(|\vec{E}|=E\) ab und berechnen den Term \(E\cdot \frac{d}{U}\):
| \(d\) in m | 0,08 | 0,08 | 0,05 | 0,15 |
| \(U\) in V | 10 000 | 20 000 | 25 000 | 25 000 |
| \(E\) in \(\frac{\rm kN}{\rm C}\) | 130 000 | 250 000 | 510 000 | 160 000 |
| \(E\cdot \frac{d}{U}\) | 1,04 | 1,00 | 1,02 | 0,96 |
b) Die Konstante hat vermutlich den Wert 1.
c) Einheit: \(\left[E\cdot\frac{d}{U}\right]=\frac{\rm N}{C}\cdot\frac{\rm m}{V}=\frac{\rm N\cdot m}{C\cdot V}=1\)
d) Mit der Vermutung aus b) und dem Nachweis aus c) folgt für die elektrische Feldstärke: \(E\cdot\frac{d}{U}=1\Rightarrow E=\frac{U}{d}\)
Elektrostatisches Lackieren
Aufgabe 1
a) Beim elektrostatischen Lackieren werden die Lacktröpfchen elektrisch aufgeladen, sodass sie vom Werkstück angezogen werden.
b) Die elektrische Energie ist aufgrund der anziehenden Wechselwirkung negativ. In großer Entfernung ist die elektrische Energie gleich null und somit die gesamte Energie positiv. Aufgrund der Energieerhaltung braucht das Lacktröpfchen also auch schon anfangs eine positive Energie. Dafür muss die kinetische Energie größer sein als der Betrag der elektrischen Energie.
c) Die kinetische Energie eines Tröpfchens beträgt: \(E_{\rm kin}=\frac{1}{2}\cdot m\cdot v^2=0,5\cdot 4\cdot 10^{-12}\,{\rm kg}\cdot \left(60\,\frac{\rm m}{s} \right)^2=7,2\,{\rm nJ}\)
d) Aus einer Regression ergibt sich folgender funktionaler Zusammenhang: \(Q(r)=8900\,\frac{\rm nC}{\rm m}\cdot r\)
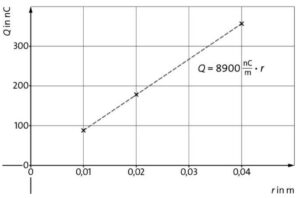
e) Mit dem funktionalen Zusammenhang von Ladung und Radius ergibt sich die Ladung für \(r=10\,{\rm µm}\): \(Q(10\,\,{\rm µm})=89\,{\rm pC}\). Damit beträgt die Energie: \(E=Q\cdot U=89\,{\rm pC}\cdot 80\,{\rm kV}=7,12\,{\rm µJ}\).
Die elektrische Energie ist ungefähr 10-mal so groß wie die kinetische Energie, daher können solche Tröpfchen das Werkstück nicht verlassen.
f) Beim zehnfachen Radius steigen die Masse und somit die kinetische Energie um den Faktor 1000 auf 7200 nJ. Die Ladung und damit die elektrische Energie steigen um den Faktor 10. Ein solches Tröpfchen wird also auch noch am Werkstück gehalten.
Auf- und Entladevorgang eines Kondensators
Aufgabe 1
a)
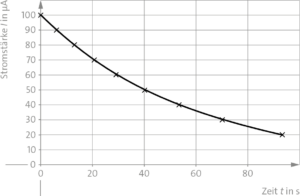
b) Den Widerstand bestimmt man aus der Stromstärke zu Beginn der Aufladung, also \(I(0\,{\rm s})\) und der Spannung \(U_0\) der Quelle: \(R=\frac{U_0}{I(0\,{\rm s})}=\frac{\rm 11,0\,V}{\rm 100\cdot 10^{-6}\,A}=110\,{\rm k\Omega}\)
c) Die Kondensatorspannung \(U_C(t)\) erhält man durch Subtraktion der am Widerstand abfallenden Spannung, d. h.:
\(U_C(t)=U_0-R\cdot I(t)\)
Man erhält folgende Werte:
| \(t\) in s | 0 | 6,1 | 13,0 | 20,6 | 29,2 | 40,1 | 53,4 | 70,2 | 93,5 |
| \(U_C\) in V | 0 | 1,1 | 2,2 | 3,3 | 4,4 | 5,5 | 6,6 | 7,7 | 8,8 |
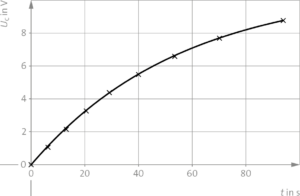
d) Die auf den Kondensator geflossene Ladung erhält man aus der Fläche unter dem \(I(t)\)-Diagramm. Unter Vernachlässigung der Krümmung des Graphen stellt die gesuchte Fläche ein Trapez dar. Damit der Fehler durch die Krümmung nicht zu groß wird, darf der Zeitpunkt nicht zu groß gewählt werden. Wir verwenden den Zeitpunkt \(t_1=6,1\,{\rm s}\). Es gilt:
\(Q(6,1\,{\rm s}=\frac{1}{2}\cdot[I(0\,{\rm s})+I(6,1\,{\rm s})])\cdot 6,1\,{\rm s}=\frac{1}{2}\cdot[100\,{\rm µA}+90\,{\rm µA}]\cdot 6,1\,{\rm s}=580\,{\rm µC}\)
Die Spannung zum Zeitpunkt \(t_1 = 6,1\,{\rm s}\) entnimmt man aus c): \(U_C(6,1)\,{\rm s}=1,1\,{\rm V}\)
Damit erhält man die Kapazität: \(C=\frac{Q(6,1\,{\rm s})}{U_C(6,1\,{\rm s})}=\frac{\rm 580\,µC}{\rm 1,1\,V}=530\,{\rm µF}\)
e) Der Messwert für den Widerstand liegt mit \(110\,{\rm k\Omega}\) gerade noch im Toleranzbereich von \(110\,{\rm k\Omega}\pm 10\,\%\). Der Wert für die Kapazität liegt mit \(530\,{\rm µF}\) noch gut im Toleranzbereich von \(470\,{\rm µF}\pm 20\,\%\).
Aufgabe 2
a) Zur Ermittlung der Halbwertszeit kann man auf geeignete Messwerte zurückgreifen. Man erhält:
| \(I_1\) in µA | 100 | 80 | 60 | 40 |
| \(I_2=\frac{1}{2}I_1\) in µA | 50 | 40 | 30 | 20 |
| \(T_H\) in s | 40,1 | 40,4 | 41,0 | 40,1 |
Als Mittelwert erhält man \(T_H=40,4\,{\rm s}\).
b) Aus der Halbwertszeit folgt: \(T_H=0,693\cdot R\cdot C \Rightarrow C=\frac{T_H}{0,693\cdot R}=530\,{\rm µF}\)
Dieser Wert stimmt sehr gut mit dem aus der Flächenbetrachtung in Aufgabe 1 bestimmten Wert überein.
Magnetisches Feld
Aufgabe 1
Gegeben: \(l=0,40\,{\rm m}\); \(n=100\); \(I=5,0\,{\rm A}\)
\(B=\mu_0\cdot I\cdot\frac{n}{l}=1,57\,{\rm mT}\)
Aufgabe 2
Gegeben: \(s=0,1\,{\rm m}\); \(B=0,056\,{\rm mT}\); \(I=0,8\,{\rm A}\)
\(F=B\cdot I\cdot s=0,0448\,{\rm N}\)
Aufgabe 3
a)
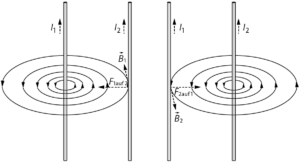
Man betrachtet hier die Wirkung des magnetischen Feldes, das von einen stromführenden Draht erzeugt wird, auf den anderen stromführenden Draht. Nimmt man an, dass durch beide Drähte ein Strom von unten nach oben fließt , dann sind die Drähte jeweils von einem ringförmigen Magnetfeld
umgeben, dessen Richtung gegen den Uhrzeigersinn zeigt. Auf den linken Draht wirkt nach der Drei-Finger-Regel eine Kraft nach rechts zum rechten Draht hin. Auf den rechten Draht wirkt eine Kraft nach links zum linken Draht hin. Die Drähte bewegen sich aufeinander zu.
b) Da die Stromrichtung in beiden Drähten gleich bleibt, bleibt auch die Richtung der Kräfte gleich und die Drähte bewegen sich aufeinander zu. Das vom rechten Draht (2) erzeugte Magnetfeld übt auf den linken Draht (1) eine Kraft vom Betrag \(F_{\rm 2auf1}=B_2\cdot I_1\) aus. Das vom linken Draht (1) erzeugte Magnetfeld übt auf den rechten Draht (2) eine Kraft vom Betrag \(F_{\rm 1auf2}=B_1\cdot I_2\) aus.
Nach dem Wechselwirkungsgesetz muss \(F_{\rm 2auf1}=F_{\rm 1auf2}\) sein. Damit ist \(B_2\cdot I_1=B_1\cdot I_2\). Einsetzen der Stromstärken \(I_1=2\,{\rm A}\) und \(I_2=0,5 \,{\rm A}\) und Herauskürzen der Leiterlänge \(s\) ergibt: \(B_2\cdot 2\,{\rm A}=B_1\cdot 0,5 \,{\rm A}\Rightarrow B_2=0,25\cdot B_1\)
Zwar ist die Stromstärke im Draht (1) viermal so groß wie die Stromstärke in Draht (2), aber gleichzeitig ist die Flussdichte um ein Viertel kleiner. Der Betrag der Kraft ist jeweils gleich groß.
Aufgabe 4
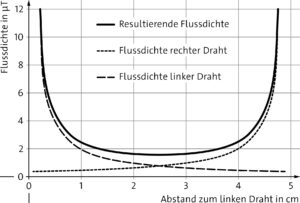
a) Die Flussdichte vom rechten und linken Draht ist zwischen den Drähten entgegengesetzt gerichtet, da die Stromrichtung in beiden Drähten gleich ist. Nahe am jeweiligen Draht ist der Betrag der Flussdichte sehr groß und nimmt dann mit dem Abstand zum Draht ab. Die Flussdichtevektoren addieren sich zu einer resultierenden Flussdichte. Nahe an den jeweiligen Drähten nähert sich die resultierende Flussdichte deshalb der Flussdichte des jeweiligen Drahtes an. In der Mitte ist die resultierende Flussdichte null, da die Flussdichtevektoren entgegengesetzt gerichtet sind und an dieser Stelle den gleichen Betrag haben.
b)
Magnetisches Feld einer Spule
Aufgabe 1
a)
| \(I_1\) in A | 0,20 | 0,40 | 0,80 | 1,00 |
| \(B\) in mT | 1,21 | 2,32 | 4,72 | 5,87 |
| \(\frac{B}{I}\) in \(\frac{\rm mT}{\rm A}\) | 6,05 | 5,80 | 5,90 | 5,87 |
Als Mittelwert erhält man \(\frac{B}{I}=5,91\,\frac{\rm mT}{\rm A}\)=0,00591\,\frac{\rm T}{\rm A}\).
Man stellt die Formel nach \(\mu_0\) um und setzt diesen Mittelwert und die weiteren gegebenen Größen in die Formel ein:
\(\mu_0=\frac{B}{I}\cdot \frac{1}{n}\cdot l\cdot \sqrt{1+4\cdot\left(\frac{r}{l}\right)^2}\)=0,00591\,\frac{\rm T}{\rm A}\cdot\frac{1}{300}\cdot 0,05\,{\rm m}\cdot \sqrt{1+4\cdot\left\frac{\rm 0,02\,m}{\rm 0,05\,m}\right)^2}=1,261\cdot 10^{-6}\frac{\rm V\cdot s}{\rm A\cdot m}\)
Der berechnete Wert stimmt im Rahmen der Messgenauigkeit mit dem Literaturwert für \(\mu_0\) überein.
b) Möglicherweise hat Paul den Sensor nicht genau in der Mitte der Spulenachse positioniert. Rechts und links der Mitte der Spulenachse nimmt die Flussdichte ab, weshalb er immer ein etwas schwächeres Feld gemessen hat.
Aufgabe 2
a) Gegeben: \(n=300\); \(r=0,02\,{\rm m}\); \(I=1,0\,{\rm A}\)
| \(l\) in m | 0,100 | 0,050 | 0,020 |
| kurze Spule \(B\) in mT | 3,499 | 5,885 | 8,326 |
| schlanke Spule \(B\) in mT | 3,768 | 7,536 | 18,840 |
b) Die Unterschiede zwischen den berechneten Flussdichten sind umso größer, je kleiner die Spulenlänge ist. Das Verhältnis vom Radius zur Spulenlänge ist umso größer, je kleiner die Spulenlänge ist. Mit zunehmender Spulenlänge wird der Term \(4\cdot \left(\frac{r}{l}\right)^2\) kleiner, und die Wurzel geht gegen 1, sodass der Unterschied zwischen den berechneten Werten immer kleiner wird.
c) Da der Wurzelterm mit zunehmender Spulenlänge gegen 1 geht, nähert sich die Formel an die für die schlanke Spule an. Deshalb gilt die Formel für die kurze Spule auch für die Berechnung der Flussdichte für eine schlanke Spule.
Helmholtz-Spulenpaar
Aufgabe 1
a) Die Flussdichte ist proportional zur Windungszahl \(n\) und zur Stromstärke \(I\). Weiterhin ist die Flussdichte umgekehrt proportional zum Radius bzw. Abstand \(r\).
b) Gegeben: \(B=2,0\cdot 10^{-3}\,{\rm T}\); \(r=0,15\,{\rm m}\); \(n=200\)
Man muss die Formel für die Flussdichte nach \(I\) umstellen und einsetzen:
\(I=\frac{B\cdot r\cdot\sqrt{125}}{\mu_0\cdot n\cdot 8}=1,67\,{\rm A}\)
Um ein Magnetfeld der Flussdichte 2,0 mT zu erzeugen, benötigt man eine Stromstärke von 1,67 A.
Aufgabe 2
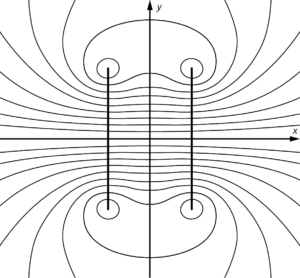
a) Die resultierende Flussdichte entlang der Spulenachse ist die Summe der Flussdichten der Magnetfelder der Einzelspulen. In der Mitte ist die Summe maximal und klingt nach außen hin ab.
b) Im Bereich von \(–0,05\,{\rm m}< x < 0,05\,{\rm m}\) ist die Flussdichte nahezu konstant und das Magnetfeld somit näherungsweise homogen.
c)
Aufgabe 3
a) Wenn die Stromrichtung in der rechten Spule entgegengesetzt der linken Spule ist, dann bleiben die Beträge der Flussdichten gleich, aber für die rechte Spule kehrt sich das Vorzeichen um. Die resultierende Flussdichte beträgt: \(B_{\rm res}=B_1-B_2\). Man kann aus der Abbildung die Beträge der Flussdichten ablesen.
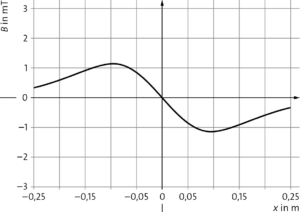
b)
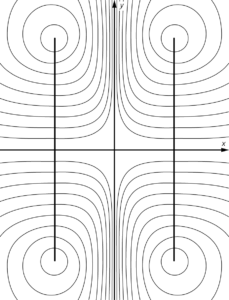
c) Die Richtung der magnetischen Feldlinien von einer der beiden Spule kehrt sich mit der umgekehrten Stromrichtung um. Da die beiden Magnetfelder der beiden Spulen nun einander entgegengerichtet sind, kommt es zur Auslöschung des Feldes in der Mitte der beiden Spulen (der Betrag der Feldstärke beider Felder ist gleich). Durch den Abstand der Spulen dominiert dann in deren Nähe das jeweilige Magnetfeld. Auf der einen Seite ist das resultierende Feld also in die eine Richtung und bei der anderen Spule in die umgekehrte Richtung orientiert. Beim Seitenwechsel kommt es deshalb zu einem Vorzeichenwechsel bei \(x=0\).
Aufgabe 4
a) Q muss an Plus und P an Minus angeschlossen werden. Dann fließt der Strom von Q ausgehend nach rechts. Die Anwendung der Rechte-Hand-Regel ergibt dann, dass die Finger der rechten Hand in die skizzierte Richtung der magnetischen Feldlinien zeigen.
b) Um die mittlere Flussdichte zu berechnen, bestimmt man zunächst über den mittleren Radius den Kreisumfang und damit die mittlere Spulenlänge \(l\):
\(U=2\cdot\pi\cdot r_m=2\cdot\pi\cdot 0,12\,{\rm m}=0,754\,{\rm m}=l\)
Mit der Formel für eine schlanke Spule der Länge \(l\) kann man die mittlere Flussdichte berechnen:
\(B=\mu_0\cdot I\cdot\frac{n}{l}=0,0015\,{\rm T}=1,5\,{\rm mT}\)
c) Die Spulenlänge und damit der Abstand benachbarter Spulenwindungen ist im Außenbereich der Spule größer als im Inneren. Die Flussdichte nimmt mit der Spulenlänge ab, die bei der Ringspule proportional zum Radius ist. Deshalb nimmt die Flussdichte vom äußeren Radius zum innersten Radius zu. Das Magnetfeld ist deshalb nicht homogen.
© Cornelsen Verlag GmbH, Berlin