Teilaufgabe 1: Wellen- und Teilcheneigenschaften von Licht
a) Die Welleneigenscchaften von Licht lassen sich besonders gut bei Interferenzexperimenten veranschaulichen. Interferenz von Lichtwellen entsteht z. B. beim Bestrahlen eines Doppelspalts mit kohärentem Licht. Auf einem hinter dem Spalt liegenden Schirm lassen sich Intensitätsextrema ausmachen, die durch die Überlagerung von Lichtwellen erklärt werden können.
b) Ein Doppelspalt eignet sich auch, um den Teilchencharakter von Licht zu erklären. Bei der Bestrahlung des Spalts mit Licht geringer Intensität kann man hinter dem Doppelspalt mit einem photonenzählenden Detektor die einzelnen Lichtquanten registrieren. Bei diesem Experiment tritt nicht sofort ein Interferenzmuster auf, wodurch man auf die Teilcheneigenschaften des Lichts schließen kann.
Teilaufgabe 2: \(h\)-Bestimmung mit dem Fotoeffekt
a) In einem Versuch zur Gegenfeldmethode des Fotoeffekts wird eine Vakuumröhre verwendet, die eine Fotokathode und eine Ringanode enthält. Zwischen Kathode und Anode wird durch eine regelbare Spannung \(U_G\) ein elektrisches (Gegen-)Feld erzeugt. Durch Variation der Spannung am Gegenfeld lässt sich die Bremswirkung auf die Elektronen kontrollieren. Im Stromkreis wird der Fotostrom gemessen. In den Strahlengang können verschiedene Filter eingebracht werden, wodurch verschiedene Wellenlängen des Lichts untersucht werden können.
b) Im Versuch wird Licht auf eine photoempfindliche Kathode gestrahlt. Die einfallenden Photonen lösen Elektronen aus der Kathode, welche sich zur Ringanode bewegen, wodurch ein Fotostrom \(I_F\) entsteht. Dieser Fotostrom wird durch ein entgegengesetztes elektrisches Feld, gesteuert durch die Spannung \(U_G\), zwischen der Kathode und einer Anode beeinflusst. Um das elektrische Gegenfeld zu überwinden müssen die herausgeschlagenen Elektronen eine minimale kinetische Energie von \(E_{\rm kin} = e \cdot U_G\) besitzen.
Mit steigender Gegenspannung sinkt die Menge an Elektronen, die die Ringanode erreichen und der Fotostrom wird geringer. Um die energiereichsten Elektronen zu bestimmen, untersucht man den Grenzfall, in dem der Fotostrom gerade auf null sinkt, also kaum noch Elektronen das Gegenfeld überwinden können. Diese maximale Energie entspricht dann \(E_{rm kin} = e \cdot U_{G,max} \).
c) Für die Frequenz des Lichts gilt:
\( f = \frac{c}{\lambda} = \frac{3,00 \cdot 10^8 \, \frac{\text{m}}{\text{s}}}{578 \cdot 10^{-9} \, \text{m}} = 5,19 \cdot 10^{14} \, \text{Hz} \).
| \(\lambda\) in nm | 578 | 546 | 436 | 405 | 366 |
| \(f\) in \(10^{14}\) Hz | 5,19 | 5,49 | 6,88 | 7,41 | 8,20 |
| \(U_{\text{G,max}}\) in V | 0,99 | 1,13 | 1,72 | 1,90 | 2,26 |
| \(E_{\text{kin}} \) in \(10^{-19}\) J | 1,58 | 1,81 | 2,75 | 3,04 | 3,62 |
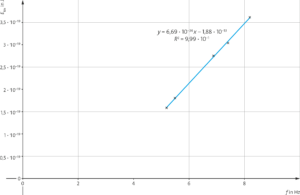
Die grafische Auswertung der Werte ergibt einen linearen Zusammenhang.
Die maximal mögliche kinetische Energie, die ein Elektron besitzen kann entspricht \(E_{\text{kin}}= e \cdot U_{\text{G,max}}\). Die Energie, die ein Photon auf ein Elektron beim Photoeffekt überträgt entspricht \(E = h\cdot f\) und muss zum Herauslösen mindestens der Auslösearbeit \(W_A\) entsprechen. Die nach dem Auslösen übrige Energie \((h \cdot f – W_A)\) entspricht der kinetischen Energie der freien Elektronen: \( e \cdot U_{\text{G,max}} = h \cdot f -W_A\).
Die obige Gleichung ist abhängig von der Frequenz \(f\) , bzw. der Wellenlänge \(\lambda = \frac{c}{f}\) des Lichts, aber nicht von der Intensität.
Die Steigung der aufgetragenen Werte im \( f\)-\(E_{\text{kin}} \)-Diagramm entspricht dem Planck’schen Wirkungsquantum \(h\) und kann zu \(h = 6,69 \cdot 10^{-34} \text{Js} \) bestimmt werden.
Die minimalen Photonenenergie, bei der gerade noch Elektronen aus der Photokathode ausgelöst werden entspricht genau der Auslösearbeit \(W_A\). Um die Frequenz des eingestrahlten Lichts zu bestimmen wird diese mit der Energie eines Photons gleichgesetzt: \(h \cdot f_{\text{min}} = W_A \Leftrightarrow f_{\text{min}} = \frac{W_A}{h} = \frac{1,88 \cdot 10^{-19} \text{J} }{ 6,63 \cdot 10^{-34} \text{Js} } = 2,84 \cdot 10^{14} \text{Hz} \).
Teilaufgabe 3: \(h\)-Bestimmung mit einer Röntgenröhre
a) Es gibt zwei verschiedene Arten von Röntgenstrahlung, die durch verschiedene Prozesse in der Anode ausgelöst werden:
Das kontinuierliche Spektrum wird durch die Bremsstrahlung erzeug. Diese kommt zustande, wenn ein Elektron sehr schnell in das Anodenmaterial eindringt und von einem Atomkern so stark abgelenkt wird, dass es einen Teil seiner Bewegungsenergie verliert und als Strahlungsquant abgibt. Je nach der Stärke der Ablenkung, hat das Strahlungsquant eine andere Energie, weshalb dieses Spektrum kontinuierlich ist.
Die charakteristische Röntgenstrahlung ist lediglich ein Linienspektrum, welches dadurch entsteht, dass ein Elektron mit hoher Geschwindigkeit auf ein Atom trifft und ein Elektron aus einer inneren Atomschale herausschlägt. Beim Übergang eines Elektrons von einer höheren Schale in den freigewordenen Platz wird eine für die Atomsorte charakteristische Menge Energie in Form eines Photons abgegeben.
b) Anhand der Abbildung lässt sich erkennen, dass die Atomrümpfe des Gitters als Elementarzentren fungieren, wenn eine Lichtwellenfront mit Wellenlänge \(\lambda\) auf sie eintrifft. Dann gehen von jedem Atomrumpf neue Elementarwellen aus, die konstruktiv interferieren, wenn ihr Gangunterschied einem ganzzahligen Vielfachen der Wellenlänge entspricht. Durch trigonometrische Überlegungen, ergibt sich als konstruktive Interferenzbedingung bei einem Einfallswinkel \(\theta\) folgender Zusammenhang: \(2 \cdot d \cdot \sin\theta = n \cdot \lambda \).
c) Das Beugungsmaximum \(n\)-ter Ordnung tritt auf, wenn der Gangunterschied \(\Delta s\) ein ganzzahlgies Vielfaches der Wellenlänge des einfallenden Lichts \(\lambda\) ist: \(\Delta s = n \cdot \lambda \).
Aus der Zeichnung ergibt sich ein Gangunterschied von \(\Delta s = \overline{AB} + \overline{BC} \). Für rechtwinklige Dreiecke gilt: \(\sin \theta = \frac{\overline{AB}}{d} = \frac{\overline{BC}}{d} \). Einsetzen ergibt sich die Bragg-Gleichung: \( 2 \cdot d \cdot \sin \theta = n \cdot \lambda \).
d) Wenn beim Auftreffen der beschleunigten Elektronen auf die Anode ihre gesamte kinetische Energie in Photonenenergie umgewandelt wird, ist diese maximal. Das bedeutet, die Wellenlänge \(\lambda\) ist am kürzesten.
e) Aus Abbildung 5 lassen sich folgende Werte ablesen:
| \(U_a\) in kV | 20 | 25 | 30 | 35 | 40 | 50 |
| \(\lambda_{\text{min}}\) in \(10^{-11}\) m | 6,2 | 4,9 | 4,1 | 3,5 | 3,1 | 2,5 |
Die maximale Energie der Röntgenstrahlung ist gegeben durch \(E_R = e\cdot U_a \) und kann gegen das Inverse der Grenze der Röntgenstrahlung \(\lambda_{\text{min}} \) aufgetragen werden:
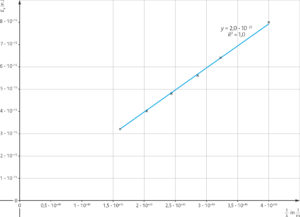
Man erkennt einen proportionalen Zusammenhang zwischen durch \(E_R = e\cdot U_a \) und \(\lambda_{\text{min}} \).
Die Röntgenstrahlung kann wie folgt ausgedrückt werden: \(E_R = h \cdot f = h \cdot \frac{c}{\lambda} \). Die Proportionalitätskonstante (Steigung) entspricht also \(h\cdot c\):
\( h\cdot c = 2,0 \cdot 10^{-25} \text{Jm} \Leftrightarrow h = \frac{2,0 \cdot 10^{-25} \, \text{Jm} }{3,0 \cdot 10^8 \, \frac{m}{s} } = 6,7 \cdot 10^{-34} \, \text{Js} \)
© Cornelsen Verlag GmbH, Berlin