Teilaufgabe 1: Materiewellen
a) Das Huygenschs’sche Prinzip besagt, dass alle Punkte auf einer Wellenfront Ausgangspunkt für eine Elementarwelle sind, welche die selbe Geschwindigkeit und Frequenz wie die ursprüngliche Wellenfront besitzt. Die neue Wellenfront ergibt sich als Einhüllende aus den Elementarwellen.
Der Spalt in Abbildung 1a kann als Ausgangspunkt einer Elementarwelle betrachtet werden, die sich kreisförmig in den geometrischen Schattenraum hinter dem Spalt ausbreitet. Das Phänomen der Beugung ist hier deutlich sichtbar.
In Abbildung 1b tritt die Beugung lediglich an den Rändern auf, wo die Welle in kreisförmigen Ausläufern in den „Schatten“ eintritt. In der Mitte des Spalts bildet die Einhüllende der vorhergehenden Elementarwellen eine ebene Elementarwelle.
b) Die Wellenlänge lässt sich mit den gegebenen Werten wie folgt berechnen:
\( \lambda = \frac{6,63\cdot 10^{-34} \, \text{J} \cdot \text{s}}{3,32 \cdot 10^{-27} \, \text{kg} \cdot 200 \, \frac{\text{m}}{\text{s}}} = 9,98 \cdot 10^{-10} \, \text{m} \approx 1 \, \text{nm} \).
Nur im leeren Raum (Vakuum) kann sich ein Teilchenbündel ohne Streuung oder andere Wechselwirkungen bewegen. Die Wechselwirkung zwischen Teilchen und festen Stoffen wird durch die Kollisionen mit den Atomen im Gitter verursacht. Deshalb können die Spalten keine Materie enthalten.
Aus den Abbildungen 1a und 1b geht hervor, dass die Beugung nur dann auffällig wird, wenn die Spaltbreite ungefähr der Wellenlänge entspricht. Die Wellenlänge, die einem bewegten Teilchen zugeordnet wird, ist umgekehrt proportional zu m⋅v . Bei einem sehr leichten und langsamen H\(_2\) -Molekül ist sie im Nanometerbereich angesiedelt. Ein schwereres Objekt hat daher eine kleinere Wellenlänge. Das bedeutet, dass auch ein viel kleinerer Spalt ohne Materie erforderlich ist, der aber wegen der atomaren Struktur der Stoffe nicht machbar ist.
c) Die Energie eines Photons kann durch die Gleichung \(E_{\rm Ph} = h \cdot f \) beschrieben werden. Für die Frequenz \(f\) der elektromagnetischen Strahlung gilt \(f = \frac{c}{\lambda_{\rm Ph}} \). Mit der Gleichung für die Energie-Masse-Äquivalenz \(E = m \cdot c^2 \) folgt:
\( m_{\rm Ph} \cdot c^2 = h \cdot \frac{c}{\lambda_{\rm Ph}} \)
\( \Leftrightarrow \lambda_{\rm Ph} = \frac{h}{m_{\rm Ph} \cdot c} \)
Teilaufgabe 2: Ein Interferenzexperiment mit Farbstoffmolekülen
a) Nach dem Huygens’schen Prinzip kann jeder Spalt des Beugungsgitters als Ausgangspunkt einer Elementarwelle betrachtet werden, die sich kreisförmig ausbreitet. Wenn die Elementarwellen, die an den Spalten entstanden sind, sich treffen und konstruktiv interferieren (maximal verstärken), treten Orte maximaler Helligkeit auf. Wenn die Elementarwellen destruktiv interferieren (sich gegenseitig auslöschen), treten Orte minimaler Helligkeit auf.
b) Wenn alle Elementarwellen, insbesondere die Elementarwellen von zwei benachbarten Spalten, konstruktiv interferieren, tritt ein Maximum auf der Detektorplatte auf.
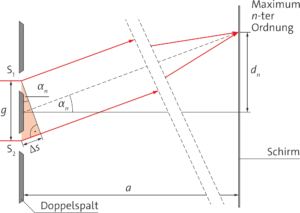
Unter der Bedingung \( g \ll a\) kann man annehmen, dass die Strecken \(\overline{S_1 P} \) und \( \overline{S_2 P} \) näherungsweise parallel sind. Das Maximum n-ter Ordnung tritt unter dem Winkel \( \alpha_n \) auf. Dieser findet sich auch in dem grau unterlegten Dreieck wieder, dessen Kathete dem Gangunterschied \( \Delta s\) entspricht.
Durch trigonometrische Beziehungen und das Ausnutzen der Kleinwinkelnäherung lassen sich der Winkel \( \alpha_n\) und die Strecken in Beziehung setzen:
\( \sin(\alpha_n) = \frac{\Delta s}{g} \approx \tan(\alpha_n) = \frac{d_n}{a} \)
Die Bedingung \(\Delta s = n \cdot \lambda \) mit \(n=0;1;2; \dots\) für konstruktive Interferenz kann eingesetzt werden und man erhält
\( \frac{n \cdot \lambda}{g} = \frac{d_n}{a} \)
\( \Leftrightarrow d_n = \frac{n \cdot \lambda \cdot a}{g} \)
c) Für den Abstand der Maxima nullter und erster Ordnung ist der Wert \( d_1 = 2,8 \cdot 10^{-5} \text{m} \) gegeben. Unter Verwendung des Zusammenhangs aus Aufgabenteil b) und der De-Broglie-Beziehung ergibt sich \( d_n = \frac{n \cdot h \cdot a}{g \cdot m \cdot v} \Leftrightarrow m = \frac{n \cdot h \cdot a}{g \cdot d_n \cdot v} \).
Einsetzen der gegebenen Werte liefert:
\( m = \frac{1 \cdot 6,63 \cdot 10^{-34} \text{Js} \cdot 564 \cdot 10^{-3} \text{m} }{100 \cdot 10^{-9} \text{m} \cdot 28 \cdot 10^{-6} \text{m} \cdot 150 \frac{\text{m}}{\text{s}} } = 8,9 \cdot 10^{-25} \text{kg} \)
Die Geschwindigkeits-Streuung \(\Delta v \) verursacht laut der Gleichung \(d_1 = \frac{1 \cdot h \cdot a}{g \cdot m \cdot v} \) eine Streuung \(\Delta d_1 \) des Abstands der Maxima nullter und erster Ordnung. Durch ein geringeres \(\Delta v\) schrumpft auch \(\Delta d_1 \) und die beiden Maxima erster Ordnung werden schmaler.
d) Zunächst treffen die Farbstoffmoleküle scheinbar willkürlich und ungeordnet auf die Detektorplatte. Mit der Zeit wird das bekannte Interferenzmuster erkannt, da sich bestimmte Bereiche auf der Detektorplatte herausbilden, die häufiger von Farbstoffmolekülen getroffen werden als andere.
e) Aus dem Zitat geht hervor, dass die Geschwindigkeit der Farbstoffmoleküle mit der Höhe h des Auftreffens zusammenhängt. Der Abstand \(d_1\) des Maximums erster Ordnung zum Maximum nullter Ordnung hängt von der Wellenlänge und somit von der Geschwindigkeit der Farbstoffmoleküle ab. Entsprechend gibt es in verschiedenen Höhen andere Werte für \(d_1\). Dies führt dazu, dass die zugehörigen Interferenzstreifen bei beiden Maxima erster Ordnung nicht parallel verlaufen.
Wegen des Zusammenhangs zwischen Geschwindigkeit v und Höhe h, treffen langsamere Farbstoffmoleküle auf das untere Ende der Detektorplatte Hier ist der Abstand \(d_1 \) ungefähr doppelt so groß wie am oberen Ende der Platte. Aus \( d_1 \sim \frac{1}{v} \) folgt: \( v_{max} \approx 2 \cdot v_{min} \).
In einem Schwerelosigkeitsversuch würden alle Farbstoffmoleküle in gleicher Höhe auf die Detektorplatte treffen. In der Mitte würden mehr Moleküle als am Rand detektiert.
Teilaufgabe 3: Detektion von Farbstoffmolekülen mittels eines Lasers
a) Die Wellenlängen auf dem Bild entsprechen der Farbe Rot. Die Photonen, die ein Farbstoffmolekül aussendet, haben höchstens die gleiche Energie wie die Photonen, die es aufnimmt. Für die Photonenenergie \( E_{\rm Ph} \) gilt folgende Formel:
\( E_{\rm Ph} = h \cdot f = h \cdot \frac{c}{\lambda} \)
wobei f die Lichtfrequenz und c die Lichtgeschwindigkeit beschreibt. E folgt, dass die Energie der Photonen umgekehrt proportional zur Wellenlänge ist. Deshalb können die Farbstoffmoleküle kein Licht mit einer geringeren Wellenlänge als die des Lasers \(\lambda_L = 661\, {\rm nm}) aussenden, also kein Licht mit einer anderen Farbe. Der Laser und die Farbstoffmoleküle senden beide rotes Licht aus. Das unerwünschte Laser-Licht kann mit Hilfe eines Farbfilters vor der Kamera absorbiert werden, sodass nur das rote Licht der Farbstoffmoleküle die Kamera erreicht.
b) Der Laser besitzt eine Strahlungsleistung von \( P_L = 50 \frac{\text{mJ}}{\text{s}} \), was bedeutet, dass pro Sekunde N Photonen emittiert werden, die eine Gesamtenergie von \( E_{\rm ges} = 50 \text{mJ} \) besitzen. Die Gesamtzahl an Photonen lässt sich damit aus der Energie eines einzelnen Photons \(E_{\rm Ph} = h \cdot \frac{c}{\lambda} \) mit den gegebenen Werten ermitteln:
\( N = \frac{E_{\rm ges}}{E_{\rm Ph}} = \frac{E_{\rm ges} \cdot \lambda}{h \cdot c} = \frac{50 \cdot 10^{-3} \text{J} \cdot 661 \cdot 10^{-9} \text{m} }{6,63 \cdot 10^{-34} \text{Js} \cdot 3,00 \cdot 10^8 \frac{\text{m}}{\text{s}}} = 1,7 \cdot 10^{17}\).
c) Um den Photoeffekt im Metall zu auszulösen, muss das Laserlicht energiereicher sein als die Schwelle der Austrittsenergie \(E_{\rm A}\) des Metalls. Laser 1 hat bei gleicher Leistung weniger, aber energiereichere Photonen als Laser 2. Wenn die Energie der von Laser 1 ausgesendeten Lichtteilchen zu gering ist, um die Austrittsenergie zu überwinden, ist es die schwächere Photonenenergie bei Laser 2 ebenfalls. Das macht Aussage A wahr. Wenn die Photonenenergie bei Laser 1 stark genug ist, um den Photoeffekt auszulösen, weiß man nicht mit Sicherheit, ob die energetisch schwächeren Teilchen von Laser 2 auch dazu in der Lage ist. Das macht Aussage B falsch.
© Cornelsen Verlag GmbH, Berlin