Teilaufgabe 1: Eigenschaften des Isotops ³²P
a) Der Kern des natürlich vorkommenden, stabilen Phosphorisotops ³¹P besteht aus 16 Neutronen und 15 Protonen.
b) Die vollständige Zerfallsgleichung für das Isotop lautet: \(^{31}\text{P}\rightarrow ^{31}\text{S}\ + e^{-} + \overline{\nu}_e \)
Einige Unterschiede zwischen β-Strahlung und \(\gamma\)-Strahlung sind:
- Die β-Strahlung hat eine geringere Eindringtiefe als die \( \gamma\)-Strahlung.
- Die β\(^{-}\)-Strahlung ist im Gegensatz zur elektromagnetischen \(\gamma\)-Strahlung eine Teilchenstrahlung, die aus Elektronen besteht.
- Die β-Strahlung wird in Magnetfeldern abgelenkt, während die \(\gamma\)-Strahlung nicht von diesen beeinflusst wird.
\(^{32}\text{P}\) entsteht durch Neutronenbeschuss aus den Nukliden \(^{32}\text{S}\) und \(^{35}\text{Cl}\) durch die folgenden Kernreaktionen:
\(^{32}_{16}\text{S} + ^1_0\text{n} \rightarrow ^{32}_{15}\text{P} + ^1_1\text{p} \)
und
\(^{35}_{17}\text{Cl} + ^1_0\text{n} \rightarrow ^{32}_{15}\text{P} + ^4_2\text{He} \)
Die zusätzlich entstanden Teilchen sind Protonen und Heliumkerne.
c) Der Aufbau des mit Gas gefüllten Geiger-Müller-Zählrohrs (GM-Zählrohrs) erlaubt der ionisierenden Strahlung durch ein Eintrittsfenster ins Innere zu gelangen. Dort werden einige Gasatome durch die Strahlung ionisiert, das heißt es werden Elektronen frei, die aus den Atomen herausgelöst werden. Die freien Ladungsträger (Elektronen und ionisierte Atomrümpfe) werden durch die anliegende elektrische Spannung zwischen dem Gehäuse und dem Draht in der Mitte getrennt. Auf ihrem Weg zum positiv geladenen Draht ionisieren die beschleunigten Elektronen noch weitere Gasatome, wodurch noch mehr Ladungsträger freigesetzt werden. Dadurch ist ein kurzzeitiger elektrischer Strom zwischen dem Gehäuse und dem Draht messbar, der einen zählbaren Spannungspuls am Widerstand verursacht. Nach dem Entladen beginnt der Prozess erneut.
Jedes Ionisationsereignis im GM-Zählrohr verursacht also einen messbaren Spannungspuls.
d) Ein GM-Zähler (Geiger-Müller-Zähler) detektiert ionisierende Strahlung, indem er die durch die Strahlung verursachten Ionisierungen in einem Gasvolumen misst. Da \(\gamma\)-Strahlung eine geringere Ionisierungsfähigkeit hat als β-Strahlung, erzeugt sie bei gleicher Strahlungsintensität weniger Ionen in dem Gasvolumen. Daher ist der GM-Zähler bei gleicher Strahlungsintensität für den Nachweis von \(\gamma\)-Strahlung weniger gut geeignet als für den Nachweis von β-Strahlung.
Die \(\alpha\)-Strahlung hat eine sehr geringe Durchdringungsfähigkeit. Das bedeutet, dass sie bereits in der Luft, in der sie sich bewegt, viele Ionen erzeugt und dadurch schnell ihre Energie verliert. Daher kann sie nur über sehr kurze Strecken (wenige Zentimeter) wirken und wird von den meisten Materialien, einschließlich der Wand des GM-Zählers, absorbiert. Daher kann nur ein sehr geringer Anteil der \(\alpha\)-Strahlung, die auf den Zähler trifft, tatsächlich nachgewiesen werden.
Teilaufgabe 2: Zerfallseigenschaften des \(^{32}\text{P}\)
a) Der radioaktive Zerfall ist ein stochastischer (zufallsbedingter) Prozess, weil man nicht vorhersagen kann, wann genau jeder einzelne Kern zerfällt. Die tatsächliche Anzahl Kernzerfälle in einem Zeitintervall \(\Delta t\) liegt in der Umgebung des Mittelwerts der zu erwartenden Kernzerfälle.
Mit den gegebenen Werten aus Tabelle 1 ergibt sich:
\( \frac{74863 + 74630 + 75003 + 74761}{4} = 74814 \) Ereignisse in \(\Delta t = 4,00 \, \text{s} \)
Das entspricht in \(\Delta t = 1,00 \, \text{s} \) einem Mittelwert von: \( \overline{N}_{\rm gemessen} = \frac{74814}{4} = 18704 \).
Aus den Angaben ist bekannt, dass die Messapparatur \( w = 2,70 %\) aller \(\beta^-\)-Zerfallsereignisse in der Probe nachweist. Damit lässt sich bestimmen, wie viele Zerfallsereignisse \(\text{n}\) insgesamt in \(\Delta t = 1,00 \, \text{s} \) stattgefunden haben:
\( n = \frac{\overline{N}_{\rm gemessen}}{w} = \frac{18704}{0,0270} = 6,93 \cdot 10^5 \)
In \( m_0 = 1,00 \, \text{mg} = 1,00 \cdot 10^{-3} \, \text{g} \) des Isotops finden insgesamt \(n_0 = 1,06 \cdot 10^{13} \) Zerfallsereignisse von \(\beta^-\)-Strahlung in einer Sekunde statt. Da lediglich das Isotop \(^{32}\text{P}\) in der Messapparatur war, lässt sich die Masse des Isotops \(\text{m}\) in der Probe bestimmen:
\( m = \frac{n}{n_0} \cdot m_0 = \frac{6,93 \cdot 10^5}{1,06 \cdot 10^{13}} \cdot 1,00 \cdot 10^{-3} \, \text{g} = 6,54 \cdot 10^{-11} \, \text{g} = 65,4 \, \text{pg} \)
b) Die Halbwertszeit kann direkt anhand des Diagramms bestimmt werden, indem die Dauer \(T_{1/2}\) der Halbierung der Probenaktivität abgelesen wird. Diese kann man zum Beispiel zwischen den Werten \( A_1 = 6,0 \cdot 10^5 \, \text{Bq} \) und \(A_2 = 3,0 \cdot 10^5 \, \text{Bq} \) ablesen:
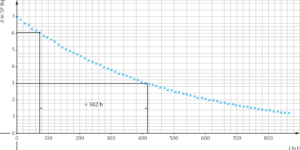
Es ergibt sich ein Wert von \( T_{1/2} \approx 342 \, \text{h} = 14 \, \text{d} \ 6 \, \text{h} \)
c) Die Anfangsaktivität der Probe aus Teilaufgabe a) beträgt \(A_0 = 6,93 \cdot 10^5 \, \text{Bq} \) und das zugehörige Isotop ³²P hat eine Halbwertszeit von \(T_{1/2} = 1,235 \cdot 10^6 \, \text{s} \).
Um den Zeitpunkt \(t\) zu bestimmen, an dem die Nachweisgrenze von \(A = 100 \, \text{Bq} \) erreicht wird, lässt sich das Zerfallsgesetz \( A = A_0 \cdot e^{-\lambda \cdot t} \) und die Formel \( \lambda = \frac{\ln(2)}{T_{1/2}} \) nutzen. Umstellen nach \(t\) ergibt:
\( t = – \frac{\ln\left(\frac{A}{A_0}\right)}{\lambda} = – \frac{T_{1/2}\cdot \ln\left(\frac{A}{A_0}\right)}{\ln(2)} \).
Das Einsetzen der bekannten Werte und der Nachweisgrenze für \(\text{A} \) ergibt:
\( t = -\frac{1,234 \cdot 10^6 \, \text{s} \cdot \ln\left(\frac{100}{6,93 \cdot 10^5}\right)}{\ln(2)} = 1,58 \cdot 10^7 \, \text{s} \approx 26 \) Wochen.
Teilaufgabe 3: Einsatz des \(^{32}\text{P}\) als Marker in der Nutzpflanzenforschung
a) Um herauszufinden, welche der beiden Gerstensorten die Nährstoffe aus dem Kunstdünger schneller aufnimmt, ist es notwendig, alle anderen Faktoren, die die Nährstoffaufnahme beeinflussen könnten, bei beiden Pflanzensorten gleich zu halten. Auf diese Weise wird allein die spezifische Eigenschaft der jeweiligen Pflanzensorte entscheidend sein.
b) Das Messen der natürlich vorhandenen Aktivität der Pflanzen vor dem hinzufügen des radioaktiv markierten Düngers soll einen Referenzwert liefern. Dieser kann dann mit der gemessenen Aktivität verglichen werden, nachdem der radioaktive Dünger zugeführt wurde.
c) Nach 7 Tagen sollten noch ein Großteil des radioaktiven Isotops \(^{32}\text{P}\) vorhanden sein, da dieses eine Halbwertszeit von 2 Wochen besitzt. Da der radioaktive Marker die gleiche Auswirkung auf die Atome beider Pflanzensorten hat, kann man durch Messen der Aktivität bestimmen, wie gut die Pflanzen den markierten Dünger aufgenommen haben. Die Pflanze, die nach 7 Tagen eine höhere Aktivität besitzt, hat mehr Phosphor aus dem Dünger aufgenommen, als Pflanzen mit geringerer Aktivität.
d) Um die gemessenen Aktivitätswerte beider Pflanzensorten sinnvoll zu vergleichen, müssen diese auf die gleiche Masse bezogen werden. Bei einer Wahl der Probemasse von \(m = 1,00 \, \text{g} \) ergeben sich für die Aktivität der Pflanzensorten folgende Werte:
| 1. Probe vor der Düngung | 2. Probe ∆t = 7 d nach der Düngung | |||
| \(m_{\text{Probe vorher}}\) in g | \(A_{\text{Probe vorher}}\) in Bq | \(m_{\text{Probe nachher}}\) in g | \(m_{\text{Probe nachher}}\) in Bq | |
| Sorte A | 1,00 | 12,7 | 1,00 | 75,5 |
| Sorte B | 1,00 | 12,1 | 1,00 | 63,7 |
Um den Aktivitätszuwachs \(\Delta A\) zu ermitteln, wird die Differenz der Aktivitätswerte vor und nach der Zugabe des radioaktiv markierten Düngers ermittelt:
Sorte A: \( \Delta A = A_{\text{nachher}} – A_{\text{vorher}} = 75,5 \, \text{Bq} – 12,7 \, \text{Bq} = 62,8 \, \text{Bq} \)
Sorte B: \( \Delta A = A_{\text{nachher}} – A_{\text{vorher}} = 63,8 \, \text{Bq} – 12,1 \, \text{Bq} = 51,7 \, \text{Bq} \)
Der Aktivitätszuwachs \(\Delta A\) ist bei Gerstensorte A ca. 21 % größer als bei Gerstensorte B. Es lässt sich schließen, dass Sorte A den Dünger schneller aufgenommen hat als Sorte B.
© Cornelsen Verlag GmbH, Berlin