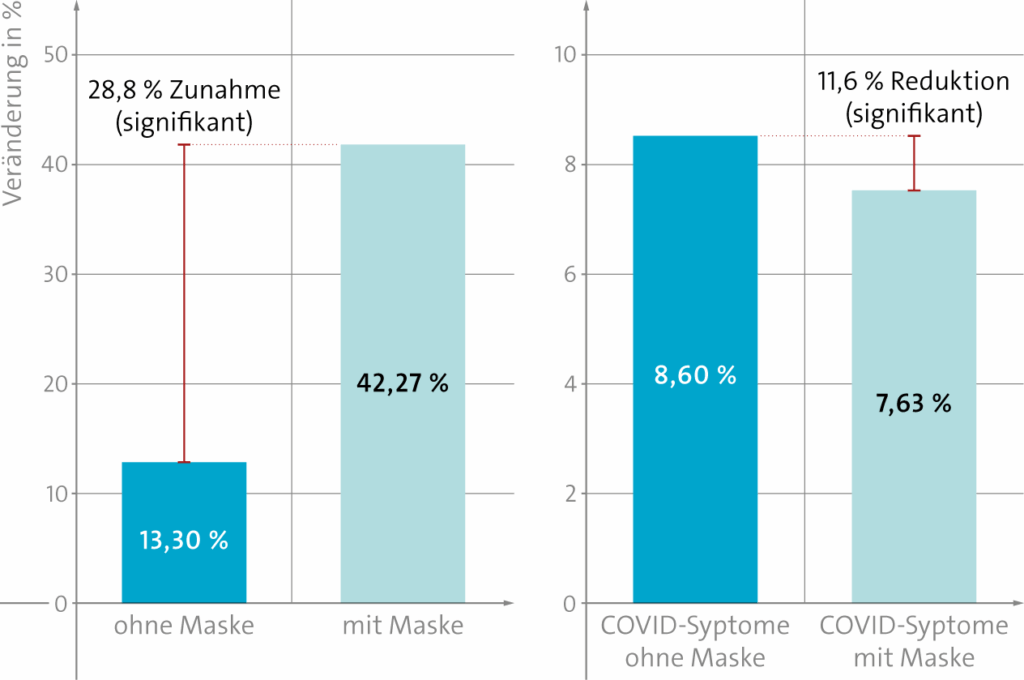
- Links wurde der Unterschied zwischen beiden Gruppen (Masketragen) mithilfe einer linearen Regressionsanalyse berechnet.
- Rechts wurde die Änderung des Auftreten von Symptomen (Prävalenz) zwischen beiden Gruppen mithilfe einer Poisson-Regression berechnet.
Warum wurden unterschiedliche Methoden genutzt?
Bei den untersuchten Größen handelt es sich um unterschiedliche Arten:
- Maskentragen ist ein prozentuales Verhalten und damit geeignet für lineare Regressionsanalyse.
- Prävalenz ist binär (ja/nein) und damit besser geeignet für Poisson- oder logistische Regressionsanalysen.
Lineare Regressionsanalyse:
Die Rohwerte sind:
- Kontrollgruppe: 13,3 %
- Maske tragende Gruppe: 42,27 %
- Unterschied der Rohdaten: 42,27 % − 13,3 % = 28,97 %, in der Grafik stehen jedoch 28,8 %
Es wurde ein lineares Regressionsmodell mit der Variable „Masketragen“ verwendet .
Zusätzlich wurden Kontrollvariablen im Modell genutzt, um andere Einflüsse außer der Werbung auf das Masketragen auszuschließen.
Bei den Kontrollvariablen kann es sich zum Beispiel um die Maskenart wie Stoff oder chirurgische Maske und das Alter der Teilnehmenden handeln.
Die Formel lautet:
- α – Maskentragequote in der Kontrollgruppe (ohne Intervention)
- β – Effekt der Intervention auf das Maskentragen
- γ – Effekt von Kontrollvariable
Durch die Anpassung mithilfe der Kontrollvariablen bekommt man dann den Unterschied zwischen Masketragen und Nichttragen von 28,8%.
Poisson-Regression
Das Prävalenzverhältnis ist ein Maß bei Beobachtungsstudien, wenn die Erkrankungswahrscheinlichkeit verglichen wird. Es ist das Verhältnis der Krankheitshäufigkeit (Prävalenz) in einer Expositionsgruppe zur Prävalenz in einer Kontrollgruppe.
Die Formel lautet: ln
μ=eα + β Symptome + γ⋅Kontrollvariablen
- 𝜇 – Erwartete Rate (z. B. Wahrscheinlichkeit, symptomatisch & seropositiv zu sein)
- 𝛼 – Basisrate (ln) der Kontrollgruppe
- 𝛽 – ln-Verhältnis des Risikos →PR = e𝛽
- 𝛾 – Effekt der Kontrollvariablen (z. B. Baseline-Symptomrate)
In der Studie:
Prävalenz in der Interventionsgruppe: 0,763 %
Prävalenz in der Kontrollgruppe: 0,860%
\[
\text{PR} = \frac{0{,}763}{0{,}860} \approx 0{,}89
\]
Das bedeutet: Die Interventionsgruppe hat 89 % des Risikos der Kontrollgruppe.
Oder anders gesagt: Das Risiko ist um ca. 11 % reduziert.