Hier findest du die Lösungen zu den Check-up-Aufgaben des Kapitels Elektrische Stromstärke, Spannung, Widerstand und Leistung.
a Hier strömen die Autos über die Autobahn. Die Stromstärke könnte man ermitteln, indem man feststellt, wie viele Autos in einer festgelegten Zeit auf der Autobahn vorbeifahren.
b Hier strömt das Wasser durch ein Wehr. Diesen Strom könnte man messen, indem man feststellt, welche Wassermenge das Wehr in einer bestimmten Zeitspanne passiert.
c Hier strömen Personen durch die Tür. Diesen Strom könnte man ermitteln, indem man die Personen zählt, die in einer festgelegten Zeitspanne durch die Tür gehen.
Die Verkehrsstromstärke wird ermittelt, indem man die Anzahl der Autos durch die festgelegte Zeit dividiert.
Es ergibt sich \(\frac{15 600\text{ Autos}}{3\ \mathrm{h}}=5 200\frac{\text{Autos}}{\mathrm{h}}\).
a Die Stromstärke wurde mit einem Stromstärkemessgerät (Amperemeter) gemessen.
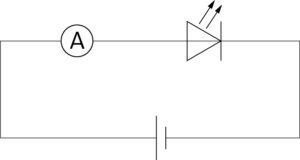
© Cornelsen\newVISION! GmbH, Bernhard A. Peter
b Gegeben:
Stromstärke \(I = 20 \, \text{mA} \)
Zeitspanne \(\Delta t = 1 \, \text{s} \)
Gesucht:
Ladungsmenge \(\Delta Q \)
Berechnung:
\(I = \frac{\Delta Q}{\Delta t} \Rightarrow \Delta Q = I \cdot \Delta t \)
\(\Delta Q = 0,02 \, \text{A} \cdot 1 \, \text{s} = 0,02 \, \text{C} \)
Ergebnis:
In einer Sekunde ist eine Ladungsmenge von \(0,02 \, \text{C} \) geflossen.
a 2,4 A = 2400 mA; 0,075 A = 75 mA; 420 μA = 0,42 mA
b 2,34 kA = 2340 A; 1200 mA = 1,2 A; 1500 μA = 0,0015 A
c 12,5 V = 12500 mV; 0,83 V = 830 mV 0,025 kV = 25 000 mV
In einem verzweigten Stromkreis (einer Parallelschaltung) ist die Gesamtstromstärke gleich der Summe der Teilströme. Es gilt also: \(I_{\text{ges}} = I_1 + I_2 + I_3.\)
\(I_{\text{ges}} = 130\ \mathrm{mA} + 50\ \mathrm{mA} + 80\ \mathrm{mA} = 260\ \mathrm{mA}\)
a \(I=I_1 = I_2=3\ \mathrm{A}\)
b \(I_{\text{ges}} = I_1 + I_2 \Rightarrow I_1 = I_{\text{ges}} – I_2 = 3\ \mathrm{A} – 0,75\ \mathrm{A} = 2,25\ \mathrm{A}\)
c \(I = I_1 = I_2 = 25\ \mathrm{mA}\)
d \(I_{\text{ges}} = I_1 + I_2 = 2\ \mathrm{A} + 0,03\ \mathrm{A} = 2,03\ \mathrm{A}\)
a Die elektrische Spannung ist der Antrieb für die Elektronen in einem elektrischen Stromkreis. Man kann sie sich als „Druck“ vorstellen, der die Elektronen veranlasst, durch den Stromkreis zu fließen.
b Eine elektrische Spannung muss immer zwischen zwei Stellen im elektrischen Stromkreis gemessen werden, da die Spannungsmessung ein „Vergleich“ ist. Das „Vergleichen“ zweier Stellen ist nur mithilfe einer Parallelschaltung möglich.
Die Spannung teilt sich gleichmäßig auf alle 16 Glühlampen auf. Es gilt: \(U =\frac{230\text{ V}}{16} = 14,375\ \mathrm{V}.\)
a Schalten wir die Lampen parallel, so leuchten beide Lampen gleich hell, da an jeder Lampe die gleiche Spannung anliegt.
b Schalten wir die Lampen in Reihe, so leuchten diese schwächer. Die Gesamtspannung teilt sich auf die beiden Lampen auf.
Stromkreis 1: \(U_1 = 4\ \mathrm{V}\)
Stromkreis 2: \(U_2 = 8\ \mathrm{V}\)
Stromkreis 3: \(U_3 = 6\ \mathrm{V},\ U_4 = 12\ \mathrm{V}\)
Physikalisch betrachtet ist eine Batterie „leer“, wenn die Ladung in ihr nicht mehr getrennt ist, sodass keine Spannung mehr zwischen den Polen besteht, d. h., es ist keine Energie mehr gespeichert. Die Batterie enthält zwar noch genauso viel Ladung wie zuvor, sie kann aber im Stromkreis nicht mehr genutzt werden.
Die Solarzellen müssen in Reihe geschalten werden, da sich die Spannungen dann addieren. Also benötigen wir \(\frac{20\ \mathrm{V}}{0,5\ \frac{\mathrm{V}}{\text{Solarzelle}}}=40\text{ Solarzellen.}\)
a
| \(U \) in V | 0 | 2,0 | 4,0 | 6,0 | 8,0 | 10,0 |
| \(I \) in A | 0 | 1,1 | 1,8 | 2,3 | 2,6 | 2,8 |
| \(R \) in Ω | 0 | 1,8 | 2,2 | 2,6 | 3,1 | 3,5 |
b Der Widerstand der Glühlampe steigt mit steigender Stromstärke bzw. Spannung. Er ist nicht konstant. Daher gilt für die Glühlampe das Ohmsche Gesetz nicht.
① Ein dünner Draht erhöht den Gesamtwiderstand der Reihenschaltung. Die Stromstärke wird daher geringer, \(L_1\) und \(L_2\) leuchten beide dunkler.
② Wie ①.
③ Der Widerstand in der Leitung mit \(L_1\) wird größer. Die Stromstärke in diesem Teilstück wird geringer und \(L_1\) wird dunkler. Dagegen verändert sich der Widerstand in der Leitung mit \(L_2\) nicht. Die Stromstärke in diesem Teilstück ändert sich also nicht und damit auch nicht die Helligkeit von \(L_2\) (vorausgesetzt, die Spannung der Batterie bleibt gleich).
④ \(L_1\) und \(L_2\) leuchten beide dunkler. Der Gesamtwiderstand wird größer, damit wird die Gesamtstromstärke kleiner – also auch die Stromstärke durch die Lampen \(L_1\) und \(L_2\).
Die Stromstärke wird kleiner, weil der Widerstand größer wird. Bei konstanter Spannung ist die Stromstärke umgekehrt proportional zum Widerstand. Wenn der Widerstand von 100 Ω auf 1 kΩ erhöht wird, verringert sich die Stromstärke entsprechend.
a Verdoppelt man die Länge, so verdoppelt sich der Widerstand.
b Vervierfacht man die Querschnittsfläche, so verkleinert sich der Widerstand auf ein Viertel.
c Halbiert man die Länge und halbiert man gleichzeitig die Querschnittsfläche, so bleibt der gleiche Widerstand.
Gegeben:
\(P_{\text{GL}}=60\ \mathrm{W}; P_{\text{EL}}=15\ \mathrm{W}; E=1\ \mathrm{kW}\cdot\mathrm{h}\)
Gesucht:
\(t\text{ in h}\)
Berechnung:
\(1\ \mathrm{kW}\cdot\mathrm{h}= 3\ 600\ 000\ \mathrm{W}\cdot\mathrm{s}\)
Glühlampe: \(t_{\text{GL}} =\frac{3\ 600\ 000\ \mathrm{W}\cdot\mathrm{s}}{60\ \mathrm{W}}=60\ 000\ \mathrm{s}\approx 16,7\ \mathrm{h}\)
Energiesparlampe: \(t_{\text{EL}} =\frac{3\ 600\ 000\ \mathrm{W}\cdot\mathrm{s}}{15\ \mathrm{W}}=240\ 000\ \mathrm{s}\approx 66,7\ \mathrm{h}\)
Ergebnis:
Die Glühlampe kann mit \(1\ \mathrm{kW}\cdot\mathrm{h}\) fast 17 Stunden betrieben werden, während die Energiesparlampe fast 67 Stunden betrieben werden kann.
Das weniger energieeffiziente Gerät der Klasse C nimmt pro Jahr 110 kWh mehr auf als das effizientere, aber 160 € teurere Gerät.
Die jährlichen Kosten für den zusätzlichen Energiebedarf betragen:
\(110 \, \text{kWh} \cdot 0,35 \, \frac{\text{€}}{\text{kWh}} = 38,50 \, \text{€} \)
Dauer bis sich die Investition wirtschaftlich gelohnt hat:
\(\frac{160 \, \text{€}}{38,50 \, \frac{\text{€}}{\text{a}}} \approx 4,16 \, \text{a} \)
Damit hat sich der teurere Kühlschrank nach etwas mehr als 4 Jahren bezahlt gemacht. Dies liegt deutlich unterhalb der typischen Lebensdauer eines Kühlschranks von etwa 15 Jahren, sodass sich die Anschaffung des teureren Geräts auf alle Fälle lohnt.